有效利用易錯題微課提升高中數(shù)學教學效率

蘇華丹

［摘 要］高中數(shù)學易錯題的錯誤類型主要包括概念理解不清、公式理解記憶不清楚、審題不清、運算失誤、思維不嚴謹五大方面，如果不及時糾正錯誤，將會影響學生對數(shù)學知識的整體掌握，甚至會影響他們的學業(yè)成績。因此，針對易錯題，采取有效的教學方法，提升教學效率非常重要。微課作為一種新興的教學方式，以其短小精悍、內(nèi)容豐富、靈活方便、可反復使用等特點備受教育界關注。借助微課，教師可以有針對性地講解易錯題的解題方法和技巧，幫助學生更好地理解和掌握知識點。文章主要探討如何利用易錯題微課提升高中數(shù)學教學效率， 為高中數(shù)學教師提供參考。

［關鍵詞］易錯題微課；高中數(shù)學；教學效率

［中圖分類號］??? G633.6??????? ［文獻標識碼］??? A??????? ［文章編號］??? 1674-6058（2024）14-0017-04

隨著新課程改革的不斷深入以及社會的持續(xù)發(fā)展，信息技術給教育教學的發(fā)展帶來了深刻的變化。信息技術改變了教師的教學方式和學生的學習方式。微課作為一種重要的數(shù)字化教學資源，以短小精悍、指向明確、內(nèi)容豐富、靈活方便、可反復使用等特點，被廣泛應用于教育領域[1]。高中數(shù)學知識具有高度抽象、知識容量大、思維層次向理性躍遷等特點[2]，習題訓練對于鞏固知識、規(guī)范方法、培養(yǎng)能力以及發(fā)展思維至關重要[3]。易錯題作為一類典型習題，可以幫助學生診斷知識薄弱點和思維誤區(qū)，具有巨大的應用價值[4]。借助易錯題微課輔助高中數(shù)學教學，可以避免“題海戰(zhàn)術”，提高學生的錯題管理能力，使學生養(yǎng)成良好的學習習慣，同時可以提升高中數(shù)學教學效率。

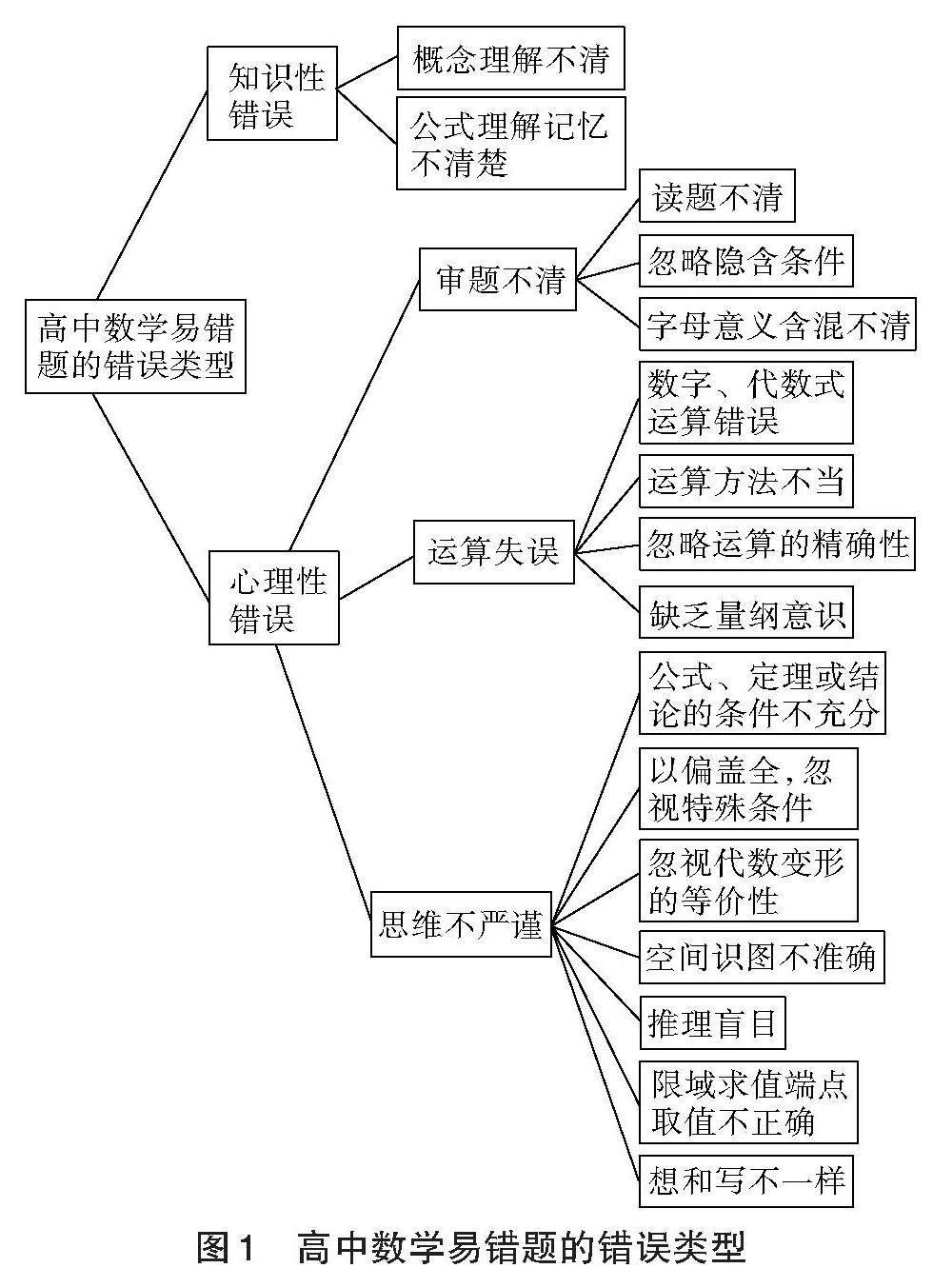
一、高中數(shù)學易錯題的錯誤類型

高中數(shù)學易錯題的錯誤類型主要包括概念理解不清、公式理解記憶不清楚、審題不嚴、運算失誤、思維不嚴謹五大方面[5]，如圖1所示。概念理解不清，即對概念的理解存在模糊、不完整或者錯誤的情況，導致無法準確應用相關概念，出現(xiàn)解題錯誤。公式理解記憶不清楚，即對公式的符號、變量理解記憶不清楚，或者對公式的推導過程或應用情境不清楚，導致錯用公式。審題不清，即在解題時沒有仔細閱讀題目，導致對題目的要求和條件理解不準確，從而影響解題。運算失誤，即在計算過程中出現(xiàn)疏忽或錯誤，導致解題出錯。思維不嚴謹，即在解題時思維不嚴謹，導致在推理和證明過程中出現(xiàn)錯誤或遺漏。

二、利用易錯題微課提升高中數(shù)學教學效率的策略

（一）利用概念型易錯題微課，深化學生對基礎概念的理解

數(shù)學概念是指數(shù)學學科中的基本概念或原理，它們是數(shù)學體系的基石。概念型易錯題微課是一種引導學生對容易出錯的基礎概念進行深化理解的微課形式。概念型易錯題微課通過向?qū)W生講解特定的基礎概念，并結合學生容易出錯的題目進行解析，幫助學生糾正錯誤，加深對基礎概念的理解。當學生在平時的學習中對數(shù)學概念的本質(zhì)理解不透徹時，就會在解題的過程中反映出來。針對容易出錯的概念題，設計概念型微課輔助講解，可以深化學生對基礎概念的理解。

例如，等比數(shù)列的概念中要求[a1]和q均不為0，但學生在解題過程中常常忽視該條件，對此教師可以將相關易錯題制作成概念型易錯題微課，并結合微課進行講解。

概念型易錯題微課的呈現(xiàn)形式如下：

［易錯題1］[x=ab]是a、x、b成等比數(shù)列的? （）。

A.充要條件

B.充分非必要條件

C.必要非充分條件

D.既不是充分條件又不是必要條件

考查要求：理解等比數(shù)列的概念。

錯誤解答：當[x=ab]時，a、x、b成等比數(shù)列成立。同時，當a、x、b成等比數(shù)列時，[x=ab]成立，所以[x=ab]為a、x、b成等比數(shù)列的充要條件，答案為A。

錯因分析：對等比數(shù)列的概念理解不清。

正確解析：當[x=a=0]時，[x=ab]成立，但a、x、b不能構成等比數(shù)列，因此充分性不成立。反之，當a、x、b成等比數(shù)列時，有[x2=ab?x=±ab]，所以[x=ab]不一定能夠成立，必要性也不成立。因此，既不是充分條件又不是必要條件，答案為D。

［變式］設a、b、c、d是非零實數(shù)，則“[ad=bc]”是“a、b、c、d成等比數(shù)列”的（）。

A.充要條件

B.充分非必要條件

C.必要非充分條件

D.既不是充分條件又不是必要條件

通過概念型易錯題微課，學生可以針對自己容易出錯的題目和概念進行有針對性的訓練和學習，從而加深對基礎概念的理解，提高解題能力和學習效果。同時，概念型易錯題微課也可以激發(fā)學生的學習興趣，促使學生對問題進行深入思考。

（二）利用公式型易錯題微課，幫助學生理解記憶公式

公式型易錯題微課是指針對特定公式的易錯題進行講解和指導的短小課程，旨在幫助學生理解和掌握特定公式的運用方法和技巧。通過公式型易錯題微課，學生可以更好地理解公式的運用方法，避免常見錯誤，并提高解題的準確性和效率。例如，在運用公式[a+b≥2ab]時，條件有“[a>0]，[b>0]，當且僅當[a=b]時等號成立”，但部分學生會忽視[a]、[b]取值均為正值和取等號的條件，還有學生將一些常用公式記為“[x2=x]”“[1x<1?x>1]”錯誤公式等。

公式型易錯題微課的呈現(xiàn)形式如下：

［易錯題2］若[x>0，y>0，x+y=1]，則[1x+4y]的最小值為（）。

A. 7???????????? B. 8???????????? C. 9???????????? D. 10

考查要求：能夠?qū)Σ坏仁焦竭M行應用。

錯誤解答：[1x+4y≥24xy≥41x+y22=8]，因此答案為B。

錯因分析：忽略了公式取等號的條件。

正確解析：因為[x+y=1]，所以有[1x+4y=x+yx+4（x+y）y=5+yx+4xy≥9]，所以答案為C。

［變式］函數(shù)[y=x+1x+1]（[x≥0]）的最小值為???????? 。

公式型易錯題微課幫助學生厘清了數(shù)學公式的易錯點，使學生能夠真正理解和記憶數(shù)學公式。借用公式型易錯題微課，結合具體實例，對數(shù)學公式中的易錯點進行分析，可以使學生深刻理解和牢固掌握知識，提高學習效果。

（三）利用審題型易錯題微課，讓學生學會審題

審題是指在解題前仔細閱讀題目，理解題目要求，明確解題思路和方法。學會審題對于解題非常重要，審題是解題的第一步，只有正確理解題目要求，才能準確地解題。常見的審題不清問題有讀題不清、忽視隱含條件、字母意義含混不清，教師可選取典型例題，通過微課的形式分別進行講解。

一是讀題不清，即沒有仔細閱讀題目或者理解題目的要求，導致在解題時出現(xiàn)錯誤或者偏離題目要求。這種情況包括遺漏題目中的關鍵信息、誤解題目的意思、錯誤理解題目的要求等。讀題不清是學生在審題過程中常見的問題之一，也是影響解題準確性和效率的重要因素。

［易錯題3］已知f（x）是R上的奇函數(shù)，且當[x>0]時，[f（x）=12x+1]，則[f（x）]的反函數(shù)的圖象大致為（）。

在解答該題時，學生很容易忽略題干中“反函數(shù)”的要求，依據(jù)函數(shù)[y=12x]在[x>0]的區(qū)間遞減以及[f（x）]過點（0，2），錯誤選擇B選項。但題干實際要求的是“反函數(shù)”，所以正確的求解為：根據(jù)函數(shù)與其反函數(shù)的性質(zhì)，原函數(shù)的定義域與值域同其反函數(shù)的值域、定義域相同，原函數(shù)中[x>0]，[0<12x<1]，[10]，故選A。

二是忽視隱含條件。忽視隱含條件指的是在解題過程中忽略了問題中未明確陳述但對問題解決具有重要影響的條件。這些條件可能并不是直接給出的，但對于問題的解決卻是至關重要的。例如在函數(shù)問題中忽視了定義域的限制；在一元二次方程求解中忽視判別式[Δ≥0]的情況等。

［易錯題4］設[α、β]是一元二次方程[x2-2kx+k+6=0]的兩個實根，求[（α-1）2+（β-1）2]的最小值（）。

A. 7??????? B. 8???????? C. [-494]??????? D.不存在

在求解此題時，學生容易忽視判別式[Δ≥0]的情況，所以會出現(xiàn)如下錯解：依據(jù)一元二次方程根與系數(shù)的關系可得[α+β=2k]，[αβ=k+6]，所以[（α-1）2+（β-1）2=α2-2α+1+β2-2β+1=（α+β）2-2αβ-2（α+β）+2=4k-342-494]，因此最小值為[-494]，答案為C。正確解析：依據(jù)一元二次方程根與系數(shù)的關系可得[α+β=2k]，[αβ=k+6]，所以[（α-1）2+（β-1）2=α2-2α+1+β2-2β+1=（α+β）2-2αβ-2（α+β）+2=4k-342-494]。因為[α、β]是一元二次方程[x2-2kx+k+6=0]的兩個實根，所以[Δ=4k2-4（k+6）≥0?k≤-2]或者[k≥3]。當[k≤-2]時，[（α-1）2+（β-1）2]的最小值為18；當[k≥3]，[（α-1）2+（β-1）2]的最小值為8。

三是字母意義含混不清。在高中數(shù)學中，字母通常被用作代表未知數(shù)或變量的符號。如果字母的意義含混不清，就會導致解題錯誤。例如，如果一個問題中使用了多個字母代表不同的變量，但沒有說明清楚它們的意義，學生可能會混淆，導致解題出錯。另外，有時候字母的意義可能會根據(jù)上下文發(fā)生變化，如果學生沒有正確理解上下文，就可能會誤解字母的意義，從而導致解題出錯。

（四）利用運算型易錯題微課，讓學生充分體會計算的重要性

運算能力是指在進行數(shù)學運算時所表現(xiàn)出來的能力，包括對數(shù)字進行基本的加減乘除等數(shù)學運算的能力，對代數(shù)式進行變形、化簡的能力，以及在運算過程中靈活調(diào)整方法、克服困難和糾正錯誤的能力。運算能力是思維能力和運算技能的有機結合，是應用數(shù)學知識解決實際問題的重要基礎。引入運算型易錯題微課的目的是幫助學生提高運算能力。通過運算型易錯題微課，學生可以在短時間內(nèi)集中學習和練習特定的運算技能，更深入地理解運算規(guī)則和方法，從而減少運算錯誤的發(fā)生。

運算型易錯題微課的呈現(xiàn)形式如下：

［易錯題5］若[a=（5，-7）]，[b=（-1，2）]，且有[（a+λb）⊥b]，則實數(shù)[λ]的值為（）。

A. 3????????????? B. [195]????????????? C. 9????????????? D. 10

考查要求：掌握代數(shù)式的相關運算方法，例如移項、合并同類項、因式分解等整式變形，繁分式化簡，無理式變形等。

錯誤解答：根據(jù)題意可知，[a+λb=（5-λ]，[-7+2λ）]，所以有[（a+λb）⊥b→（a+λb）·b=0→5-λ+2（-7+2λ）=0]，解得[λ=3]，因此答案為A。

錯因分析：在上述的計算過程中，數(shù)字的運算出錯，忽略了[（5-λ）×（-1）]時的符號，兩者相乘仍為[5-λ]，導致最終的計算結果出現(xiàn)錯誤。

正確解析：因為[a+λb=（5-λ，-7+2λ）]，所以有[（a+λb）⊥b→（a+λb）·b=0→λ-5+2（-7+2λ）=0]，求得[λ=195]，所以答案為B。

［變式］已知向量[a=（1，2）]，[b=（2，-2）]，[c=（1，λ）]，若[c]∥[（2a+b）]，則[λ=]???????? 。

（五）利用思維型易錯題微課，培養(yǎng)學生的解題思維

數(shù)學思維是指在解決數(shù)學問題時所表現(xiàn)出來的思考方式和能力。當面對復雜的數(shù)學問題情境時，學生很容易因為思維不嚴謹而導致解題出錯，例如以偏概全，重視一般性解題而忽略特殊情況。

思維型易錯題微課的呈現(xiàn)形式如下：

［易錯題6］數(shù)列[an]的前[n]項和為[Sn=n2-2n+3]，則[an=]???????????????? 。

考查要求：分類討論求解數(shù)列。

錯誤解答：根據(jù)題意，可以有[an=Sn-Sn-1=（n2-2n+3）-（n-1）2-2（n-1）+3=2n-3]。

錯因分析：忽視[n=1]的情況。

正確解析：根據(jù)題意，可以有當[n≥2]時，[an=Sn-Sn-1=（n2-2n+3）-（n-1）2-2（n-1）+3=2n-3]，而[a1=S1=2]不適合上式，∴[an=2，n=1，2n-3，n≥2。]

［變式］[Sn]為數(shù)列[an]的前[n]項和，若[an>0]，[an2+2an=4Sn+3]，則[an]=?????????????? 。

新高考改革突出知識為基、能力為重，堅持素養(yǎng)導向和價值引領。在新高考背景下，教師利用微課講解易錯題這一新教學模式，打破了傳統(tǒng)的數(shù)學教學模式，使得學生“學習習慣不良與錯題重要性認識不足”和教師“授課進度緊張與錯題講解效率低下”等問題得到了有效解決，不僅幫助學生改善了學習習慣，使學生能夠自主思考和主動學習，還強化教師對學生易錯題的教學管理，提高了教師的教學效率。

［?? 參?? 考?? 文?? 獻?? ］

[1]? 張家文.利用微課提高高中數(shù)學習題課教學的有效性[J].數(shù)理天地（高中版），2023（13）：89-91.

[2]? 朱云飛，蔡薇.微課背景下的高中數(shù)學錯題管理策略探析[J]. 理科考試研究，2023（9）：29-31.

[3]? 黃燕.高中數(shù)學復合函數(shù)習題教學探究[J].中學教學參考，2021（2）：8-9.

[4]? 史宇宙.高中數(shù)學課堂利用易錯題提升教學質(zhì)量的建議[J].新智慧，2017（31）：21.

[5]? 沈宏.高中數(shù)學易錯題的分類與成因分析[J].中學數(shù)學月刊，2015（12）：54-56.

（責任編輯??? 黃春香）

［基金項目］南寧市教育科學“十四五”規(guī)劃2021年度“高中數(shù)學易錯題AR化應用研究”課題（立項編號：2021C127）。