基于學生認知邏輯的初中數學“勾股定理”教學應用研究

摘 要：學生認知邏輯作為初中數學教學的基礎，在“勾股定理”教學中具有突出價值。首先對學生認知邏輯，特別是初中生的認知邏輯進行分析，然后從輔助學生構建表象、深化學生認知理解、鼓勵學生主動驗證猜想、促進學生由一般到具體的邏輯推理回歸等方面著手，研究基于學生認知邏輯的初中數學“勾股定理”教學策略，希望能為初中“勾股定理”教學提供參考。

關鍵詞：學生認知邏輯；初中數學；勾股定理

作者簡介：夏兆陽（1975—），男，江蘇省徐州市百川學校。

勾股定理是初中數學的核心知識點。在蘇科版《數學》八年級上冊中，“勾股定理”章節的主要內容為勾股定理的概述、逆定理和簡單應用。這一章節對學生的認知邏輯有較高要求，因此，研究基于學生認知邏輯的“勾股定理”教學具有非常重要的意義。

一、學生認知邏輯概述

學生認知邏輯是學生在學習過程中逐漸形成的認識事物的方法，表現為特定的認知順序和規律，也反映出學生特定階段的學習需求［1］。從關注重點來看，學生認知邏輯聚焦于學生在學習期間的思維方式和推理模式，特別是學生理解、掌握知識的過程。從特征表現來看，學生認知邏輯具有由小及大、由近及遠、由特殊到一般、由具體到抽象的特點，并且會隨著時間的推移逐步成熟、完善。

在初中階段，學生處于個體身心發展的第二高峰期，生理發展為其認知發展提供了物質前提，他們的有意想象能力、記憶力、思維能力快速發展，認知邏輯結構體系基本形成［2］。在這一階段，學生思維活動的基本特點是抽象邏輯思維逐步占據主導地位，屬于經驗型的邏輯思維階段，但仍然依賴感性經驗的直接支持，辯證邏輯思維和創造邏輯思維具有較大的發展空間。具體表現為學生能夠初步運用邏輯推理和抽象概念來解決問題，思維的方向性、目的性更加明確，但尚不足以在大量理論的指導下分析、整合各種事實材料。

二、基于學生認知邏輯的初中數學“勾股定理”教學策略

（一）設置前置補償，輔助學生構建表象

勾股定理本身具有較為清晰的表述對象和元素關系，有利于學生理解和記憶。相較于具有一般抽象意義的“a2+b2=c2”，學生更容易理解“勾三股四弦五”這樣的具體描述［3］。根據學生認知邏輯“由特殊到一般”的特點，教師可以設置前置補償，幫助學生構建關于勾股定理的表象。勾股定理的表象是感性反映的高級形式，常表現為客觀層面的概念、組成命題、逆命題、模型以及各種幾何圖形等。借助前置補償，學生可以在頭腦中形成對勾股定理的大致印象，為后續解題實踐奠定基礎。在設置前置補償時，教師應立足數學定理“從事實中歸納出來”的特點，從解決具體問題著手，設計練習題，幫助學生突破難點，如以下例題。

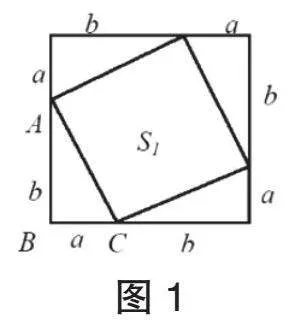
【例題】根據圖1，可知S△ABC=（ ），S1=（ ），S大正方形=（ ）。

學生可以獨立或合作解答前置補償題，從中初步了解勾股定理的表象。接著，教師可以立足于學生的情感體驗，設置“數方格”的自主學習任務，要求學生數一數直角三角形兩條直角邊a和b組成的正方形與斜邊c組成的正方形所占的小方格數量，引導他們從圖形角度思考并尋找一般規律：直角三角形兩條直角邊的平方和等于斜邊的平方。通過趣味數數，多數學生能輕松算出直角三角形三條邊a、b、c分別組成的正方形面積S1、S2、S3，并得出S3等于S2與S1的和。在學生了解一般規律后，教師可以設計前置合作聯系模塊，鼓勵學生根據已有的知識經驗，借助割補法進一步推導等量關系，即邊長為a+b的大正方形的面積等于邊長為c的小正方形的面積加上四個直角三角形△ABC的面積。隨后，教師可以將方格圖中的背景線擦除，要求學生在無法直接獲得邊長a、b和面積S2、S1的情況下，根據前提條件“Sa+b=Sc+4SRt△ABC”，發散思維，借助自身想象力聯系a、b、c三個特殊的數值與三角形形狀，由特殊跨越到一般，構建直角三角形三邊關系的表象。

（二）設計問題鏈，深化學生認知理解

經過前置練習和語言引導后，多數學生都能對勾股定理的表象形成基本認識，可以接受基于“由特殊到一般”認知規律的教學指導，了解勾股定理的結論。但部分學生仍停留在“知其然而不知其所以然”的層面，具體表現為未經歷數學知識、問題、結論及解題思路被發現和創造的過程，對數學缺乏真正的理解［4］。問題鏈是彼此關聯且有序的問題串，其整合了一組有中心、有序列、有層級、有聯系、有獨立性的問題。問題鏈可以將“勾股定理”教學轉化為學生思考和探究問題的過程，引導學生進一步深入認識勾股定理。因此，教師可以圍繞發現、分析和解決問題的思維邏輯，設計以勾股定理為中心的問題鏈，幫助學生鞏固所學知識，使其不僅“知其然”，還“知其所以然”。問題鏈如下：

①在任意△ABC中，三邊a、b、c間有何數量關系？

②在Rt△ABC中，除了|a-b|lt;clt;a+b，三邊a、b、c間的數量關系還有哪些？

③能否用4個全等三角形拼成正方形，通過面積關系證明直角三角形兩條直角邊a、b的平方和等于斜邊c的平方？

提出問題②后，教師應提示學生考慮直角三角形的特殊性質，帶領學生回顧直角三角形的特性，這有助于他們理解直角三角形三邊間的特殊關系［5］。當學生陷入思維瓶頸時，教師可以適時引導學生轉換思維，從一次方轉移到二次方情形，即a2+b2-2ablt;c2lt;a2+b2+2ab。在展示上述不等式后，教師可以要求學生用一個等式表示a、b、c之間的關系并闡述理由。比如，某學生運用所學知識，通過邏輯推理得出a2+b2=c2，并補充理由：因為a2+b2-2ablt;c2lt;a2+b2+2ab呈對稱性，所以c2的理想狀態為中點位置，等于兩端a2+b2-2ab、a2+b2+2ab的平均數。

在這一問題鏈引導中，學生將經歷自主探究、合作討論、歸納類比、推理論證等過程，提高邏輯推理能力，逐步實現對勾股定理的深入理解。

（三）打造邏輯探究階梯，鼓勵學生主動驗證猜想

在學生通過自學與解題逐步加深對勾股定理的理解的過程中，教師可以借助數學課件制作軟件——Sketchpad幾何畫板，打造邏輯探究階梯，充分發揮幾何畫板作圖便捷、動態演示的優勢，鼓勵學生驗證猜想［6］。打造邏輯探究階梯的第一步，教師可以演示Rt△ABC三邊a、b、c分別組成3個正方形的動畫。其中，正方形CBFG的邊長為a，正方形KACH的邊長為b，正方形ABDE的邊長為c，面積分別5.98 cm2、1.74 cm2和7.72 cm2。在演示過程中，教師可以逐步指導學生觀察和測量，設定正方形的面積并標注三邊a、b、c的長。通過觀察動畫，學生能夠直觀得出結論：正方形ABDE（面積為c2）的面積等于正方形KACH（面積為b2）與正方形CBFG（面積為a2）之和，由此推導出Rt△ABC的直角邊a、b的平方和等于斜邊c的平方。

打造邏輯探究階梯基礎后，教師可以繼續引導學生利用幾何畫板構建由特殊到一般的邏輯階梯。在這一階段，教師可以演示4個全等直角三角形Rt△ADH、Rt△AEB、Rt△DGC、Rt△BCF圍成一個大正方形HGEF和一個小正方形ABCD的過程，其中大正方形HGEF的邊長為a+b，小正方形ABCD的邊長為c。借助幾何畫板，教師可以要求學生計算大正方形HGEF的面積，并發現它等于小正方形ABCD的面積與4個直角三角形的面積之和。

在幾何畫板演示的過程中，學生可以從特殊情形出發，通過面積分析和拼湊驗證勾股定理的等量關系，搭建由特殊到一般的邏輯階梯。這一探索過程能幫助學生經歷驗證勾股定理猜想的過程，掌握拼湊法、分割法的技巧，鍛煉空間想象力和邏輯推理能力。

（四）整理常見易錯題型，促進學生由一般到具體應用的邏輯推理回歸

“勾股定理”教學的重點是理解直角三角形三邊之間的數量關系，掌握將直角三角形的特征轉化為數量關系的技巧。在初中階段，勾股定理的主要應用是通過已知直角三角形的任意兩條邊來求解第三邊，而在實際應用中往往需要對問題進行變形處理，導致學生錯誤頻出［7］。基于此，教師可以結合初中生在辯證邏輯思維和創造性邏輯思維方面的不足，從辯證對比的視角整理關于勾股定理的常見易錯題型，如求邊長、求方程、求梯子下滑問題等。整理錯題后，教師可以將學生分成四人小組，要求各組合作討論解題，分析錯誤原因并總結規避路徑，以提升學生解決實際問題的能力。易錯題型具體如下。

（1）求邊長的易錯題型：假設一個直角三角形的兩條邊長分別為9和15，那么第三條邊長是多少？

在解答此問題時，多數學生容易忽略分類討論，直接默認15是斜邊，僅考慮一種情況。為避免類似錯誤，教師可以鼓勵學生在小組內分享交流解題錯誤的原因，提出個性化建議。例如，可以通過畫圖討論直角邊和斜邊的關系，優先考慮多種可能的情況。

（2）求方程的易錯題型：有一個長方體池塘，池塘的底面是正方形，邊長是10 m，池塘正中有一 根水草，水草長度超出水面1 m。如果將這根水草拉向池塘一邊終點，水草頂端恰好到達池塘邊的水面，設水草的高度為x，則列方程可得（ ）。

求方程的重點在于分析數量關系、設置未知數，并利用勾股定理列出正確的方程。在解答過程中，部分學生缺乏模型思維，難以構建直角三角形并表示三邊的數量關系；部分學生難以將文字信息轉化為圖形，無法找到幾何圖形中的數量關系；部分學生不知道如何分析水草高度和水面高度的關系，無法得出池塘中心到邊緣的距離，難以找到方程的等量關系。為解決這些問題，教師可以通過展示水草長度和池塘深度關系的動畫（保持水面平行于池塘底面），幫助學生直觀理解變量和不變量的關系，掌握利用勾股定理列方程的方法。

（3）梯子下滑問題的易錯題型：一根梯子NM長5 m，頂端N靠在墻NO上，梯子下端M與墻角G的距離為3 m，在梯子下滑后停留在HF位置，測得底端HG的長度為1.8 m，則梯子頂端N沿墻下滑了多長距離？

在解答過程中，許多學生將梯子頂端的下滑距離誤認為是底端的移動距離，忽略了題中隱含的條件，缺乏對圖形的多角度理解。為規避類似錯誤，教師可以小組合作學習的形式，引導各小組分析已知條件，論述兩個直角三角形中已知的邊長，討論如何求解邊長與線段NF的關系。然后，將NF分解為兩條線段長度的差，找到梯子長度這一不變量，根據勾股定理列方程求解。

通過對易錯題型的整理與師生、生生之間的討論分析，學生可以逐漸搭建起勾股定理在幾何圖形與數量關系間的橋梁，完成由一般到具體應用的邏輯認知轉化。

結語

綜上所述，學生的認知邏輯具有由一般到具體的特點，初中生的認知邏輯結構已基本形成，認知活動的自覺性顯著增強，認知與個性得到協調發展，但在辯證邏輯思維和創造性邏輯思維方面仍存在不足。根據初中生的認知邏輯特點，教師可以制訂適合的初中數學“勾股定理”教學策略，以滿足學生的個性化學習需求，為提升教學效率提供有力保障。

［參考文獻］

占鵬飛.基于學生認知邏輯的高中地理課堂教學：以“大豆資源安全”為例［J］.地理教學，2024（8）：58-60.

張紅，祁璐，漆潘艷，等.勾股定理的數形表征與教學設計［J］.教育科學論壇，2021（34）：54-58.

黃秀旺.翻轉課堂：促進學生學習自動力的提升：以蘇科版初中數學教科書八年級上冊“3.1勾股定理”教學為例［J］.華夏教師，2023（10）：82-84.

謝雅禮，謝曉瑜.讓學生深信自己的智慧和力量：從“發現勾股定理”的教學設計談“啟導·探究·發現”教學法［J］.創新人才教育，2022（2）：74-79.

吳立寶，宋雯茜，王子續，等.促進深度學習的逆向數學單元作業設計：以“勾股定理”為例［J］.數學教育學報，2024，33（2）：14-19.

徐小琴.數學文化中融入“課程思政”的“導講研思”教學模式：以數學文化中的勾股定理為例［J］.內江師范學院學報，2024，39（4）：1-6.

孫悅，劉金魁.新課標下初中數學教學案例設計：以“探索勾股定理”為例［J］.凱里學院學報，2020，38（6）：109-111.