對當前初中生數學思維能力現狀的研究和思考
周洪亞
摘 要: 思維能力是學習對象學習能力水平的重要內涵,是學習對象智力水平的重要特征。本文通過對學習對象思維能力水平的研究和分析,對當前初中生數學思維能力水平發展現狀進行了研究分析,并就如何做好思維能力培養工作進行論述。
關鍵詞: 初中數學教學 數學思維能力 培養途徑
一、初中生數學思維能力現狀
思維能力是學習對象學習能力水平的重要內涵,是學習對象智力水平的重要特征。新課程標準強調指出,要將學習能力培養作為有效教學的第一要務。但由于應試教育和升學壓力的影響和制約,以分數論“英雄”的傳統教學活動重視學生解題活動教學,忽視思維能力水平培養,初中生思維能力水平的現狀主要呈現以下特征。
一是主動思維意識淡薄。部分初中數學教師在應試教育“大棒”的驅使下,忽視學習對象思維能動情感的激發,采用單一、單向、傳統的教學模式。一方面不能將自身具有的引導、指導特性充分發揮,另一方面不能充分利用數學學科隱含的豐富情感教學資源,營造輕松、融洽的教學氛圍,引發學生主動思考分析的潛能和欲望,導致初中生不愿開展思考、分析和歸納等思維活動。
二是缺少思維實踐活動時機。部分初中數學教師過分強調教師的主導作用,將課堂教學中的師生雙邊活動變革為教師講解為主的單向活動,學生主體能動特性受到壓制,只能被動接受教師“直接”灌輸的知識經驗,缺少自主探究實踐的活動時機,面對實際問題“手足無措”。
三是解析方法不夠靈活。部分初中生在感知、分析、解答數學問題案例的過程中,由于未能掌握思考、分析、解答問題的基本方法和規律策略,圍繞問題案例解答要求,不能正確對問題條件及解題要求之間的關系進行深入探析,對解答問題的思路不能進行科學、全面規劃。特別對較復雜的數學問題,不能根據已掌握的解題方法進行“變通”和創新,不能運用靈活的解題方法解答問題案例。如在全等三角形的判定案例教學中,判定三角形全等的方法有好幾種,但學生面對實際問題時,對如何判斷三角形全等的方法產生疑惑,不能結合問題要求,采用多種多樣的判斷方法證明其全等,根本原因在于學生對判斷的方法運用不夠靈活。
四是綜合歸納技能薄弱。數學學科知識點關系緊密、關聯深刻,是一個緊密聯系的有機整體。囊括多個知識點的綜合性問題,在問題案例解答中經常出現,但初中生在解析該類型問題案例時,運用多種解題策略或解題思想方法等技能素養還較低,綜合歸納、邏輯推理等方面的思考判斷能力需進一步提高,綜合歸納的思維技能較薄弱。
二、培養初中生數學思維能力的途徑
針對初中生數學思維能力的現狀及問題,我認為應從以下方面著手進行有效解決。
一是利用豐富的情感資源,挖掘主動思維潛能。數學是思維的藝術,其發展進程及自身內容有著顯著而鮮明的生動特性、現實特點、應用意義和趣味特征。數學學科的豐富情感資源為消除初中生思維活動的“消極”思想,堅定主動思維信念,提供了有利條件,奠定了堅實基礎,將學生引入到主動思考、分析、探析問題的活動中。生活性是數學學科的最基本特性,任何社會、生活領域總能找尋到數學知識的“蹤影”。同時,初中生對貼近現實生活的案例充滿“親近感”,成為驅動和激勵學生主動思維的有效抓手。如在“正比例函數”案例教學中,教師為吸引學生注意力,調動其思維積極性,為其創設了“電信公司設置不同方案銷售通訊費用”、“工人師傅向游泳池注水,注水時間和水位高度之間的關系”等現實生活情境,引發了學生的情感“共鳴”,帶著積極情感主動思考分析問題案例。
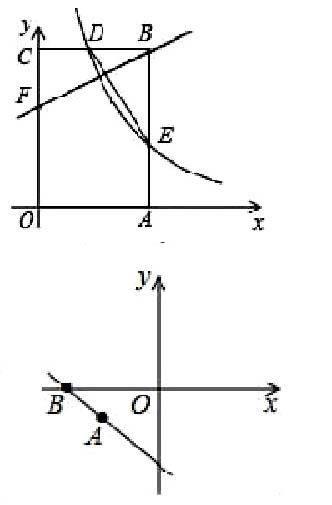
二是搭建實踐探析載體,提供思考分析時機。學習能力的培養離不開實踐探究的活動進程。初中生思維能力水平不高的一個重要方面,就是缺少直接實踐、探析的活動過程。這就要求初中數學教師騰出一定的教學時間搭建具有實踐探析意義的活動載體,提供學生進行思考、分析和探究的活動時機,引導學生將所學知識內容轉化為思考探究的方法經驗,指導學生深刻地思考分析解答問題案例,獲得解決問題的方法和策略,形成思考分析解答問題的經驗技能。如在“如圖,矩形BC的頂點A,C分別在x軸和y軸上,點B的坐標為(2,3)。雙曲線y=k/x(x>0)的圖像經過BC的中點D,且與AB交于點E,連接DE。求k的值及點E的坐標”的案例教學中,教師采用“探究性教學策略”,學生探析問題條件內容后,根據解題要求,展示其思考分析過程:“根據B的坐標,以及四邊形ABCO為矩形,確定出BC中點D坐標,代入反比例解析式求出k的值;根據E在反比例圖像上,且B與E橫坐標相同,確定出E坐標即可。”教師對學生的解題思路進行實時指導,在其解答活動后,引導、指導其歸納總結解題策略。此案例教學過程中,學生獲得思考、分析、解析問題解答思路、解題策略的實踐探究活動,掌握思考分析問題的一般方法和策略,思維能力得到有效鍛煉和提升。
三是重視解題方法傳授,提高思維能力。初中數學學科案例解答的思想策略有函數與方程的思想、數形結合的思想、分類討論的思想、轉化與化歸的思想等,基本方法有換元法、配方法、構造法、待定系數法、公式法及反證法等。教師在思維能力培養中要重視解題方法的傳授,一方面設置具有典型特征的問題案例,另一方面結合案例進行針對性講解,向學生傳授解題方法的內涵、要義及注意點,使學生能夠真正認識和掌握解題方法的精髓,正確、高效地應用于問題解答活動。如在“如圖,直線y=kx+b經過A(-2,-1)和B(-3,0)兩點,則不等式組1/2x 四是注重綜合問題教學,提高綜合思維素養。初中數學教師應抓住數學知識點之間的深刻聯系,設置具有綜合特性的數學問題,引導學生結合多種解題方法進行分析、解答問題活動,指導學生根據題意選擇和應用多種多樣的解題方法或策略,正確、完備地解決綜合性數學問題,提高初中生綜合應用的思維能力。

