例談小學數(shù)學教學中復合應用題的解法

趙娜

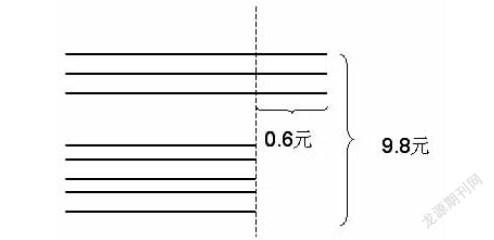
摘 要： 應用題是小學數(shù)學的重點和難點，也是大多數(shù)學生難以解決的問題。特別是復合應用題對部分學生來說簡直是“望題興嘆”，作者就復合應用題的解題方法結合自己的教學經(jīng)驗進行歸納。

關鍵詞： 小學數(shù)學教學 復合應用題 解題思路

應用題是小學數(shù)學的重點和難點，也是大多數(shù)學生難以解決的問題。復合應用題概括起來可以分為一般的解題思路和特殊的解題思路兩種。

1.一般的解題思路

復合應用題實際上是由若干個簡單應用題組合而成的。按照思維過程的不同，一般解題思路可以分為兩種：綜合法和分析法。

（1）綜合法，是由已知條件引導到未知，即由條件推到結論的推理方法。

（2）分析法，是由未知追溯到已知，即由結論回到條件的推理方法。

采用分析法的解題思路，是從應用題的問題入手，根據(jù)數(shù)量關系，找出解答這個問題所需要的兩個條件；然后把其中的一個（或兩個）未知的條件作為要解的問題，再找出解答這一個（或兩個）問題所需要的條件；這樣逐步逆推直到所找的數(shù)量在應用題中都是已知的為止。在這樣的推導過程中，同樣也得到兩個結果，一組相互關聯(lián)的簡單問題，以及解答這一組簡單應用題的順序。

2.特殊的解題思路

有些應用題具有特殊的數(shù)量關系，如果按照前面的一般解題思路，不容易找到解答方法，往往需要采用一些特殊的解題思路尋求解答方案。下面舉例介紹幾種常用的特殊解題思路。……