小議高中數(shù)學教學中習題教學的反思

董朝芳

摘 要：數(shù)學是學生在高中階段的重點和難點學習科目，其教學方法至關(guān)重要。尤其是在習題教學上，目前存在著較多的問題，需要進行反思。本文首先分析了目前在高中數(shù)學習題教學中存在的突出問題，并闡述了問題出現(xiàn)的原因。然后結(jié)合以往的教學經(jīng)驗，總結(jié)了幾條針對性的改進策略，為后期提升教學質(zhì)量提供參考和借鑒。

關(guān)鍵詞：高中數(shù)學；習題教學；問題；策略

中圖分類號：G622 文獻標識碼：B 文章編號：1002-7661（2016）06-071-02

一、目前高中數(shù)學習題教學中存在的問題

1、題量和質(zhì)量不統(tǒng)一。很多老師認為只要加大題量，讓學生不斷練習就能夠充分的掌握相關(guān)知識，這種想法存在根本性的錯誤。習題教學依靠的不僅僅是數(shù)量，更重要的是習題的質(zhì)量。本來高中數(shù)學就存在一定的難度，學生的壓力非常大，而老師又安排學生重復練習同一類題目，這就導致學生產(chǎn)生一定的厭煩心理。

2、習題的題型太過單一。單一性的練習只能夠提高學生對某個知識點的掌握能力，卻不利于對于數(shù)學知識的全面掌握，那么在進行實際考試檢測的過程中，還是難以拿到高分。并且，題型太多單一也不利于學生邏輯思維能力的培養(yǎng)和提升，無法成長為一名適合社會發(fā)展的綜合型人才。

3、忽略了學生的主體地位。在習題教學過程中，學生是主體，而老師需要發(fā)揮自身的引導作用。但是很多老師并沒有正確看待這一問題，總是讓學生機械的按照自己的意愿和安排進行習題練習，忽略了學生的主觀感受以及學生總體數(shù)學水平參差不齊的現(xiàn)實性問題。

4、教學方法比較落后。隨著多媒體技術(shù)的發(fā)展，為教學活動提供了諸多便利，老師在課堂上可以充分借助多媒體是被，完成高質(zhì)量的教學任務(wù)。但是很多老師受到傳統(tǒng)教學思維的限制，并沒有將習題教學和多媒體技術(shù)進行結(jié)合。比如在一些比較抽象的數(shù)學知識講解上，只依靠口頭的講解學生不容易理解，那么老師就可以利用媒體技術(shù)從網(wǎng)絡(luò)上調(diào)出動態(tài)圖像，加深學生的理解和對知識點的掌握[1]。

二、提升高中數(shù)學習題教學的策略

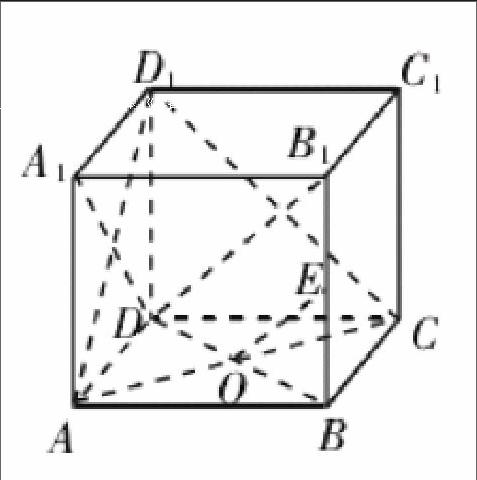
1、深化教學方法，培養(yǎng)學生的思維能力。思維能力的提升有助于學生掌握一些比較難的數(shù)學知識點，并增加其對數(shù)學學習的興趣。在習題教學中，老師要善用分析法和類比法，讓學生從思維定勢轉(zhuǎn)變?yōu)閿U散性思維，從而使他們可以更加深入的理解數(shù)學課本上提出的各種理論知識，并加深記憶，還有利于掌握更加靈活的運用方法，做到舉一反三。教學案例：在正方體ABCD--A1、B1、C1、D1中，E是BB1的中點，O是底面正方形ABCD的中心，求證：OE⊥平面ACD1。

本題考查的是學生對線面垂直能不能作出準確的判斷。學生要想證明OE⊥平面ACD1，就首先要正面OE和平面ACD1中的兩條直線是相互垂直的關(guān)系。在解答這道習題的過程中，學生需要進行思維的轉(zhuǎn)換，用線線關(guān)系替代原本的線面關(guān)系。由此可見，轉(zhuǎn)換性思維能力在數(shù)學學習過程中發(fā)揮著至關(guān)重要的作用，老師應(yīng)該多給學生布置類似習題的練習，逐漸提升他們的思維轉(zhuǎn)換能力[2]。

2、優(yōu)化數(shù)學習題。進行習題教學時，老師不應(yīng)該盲目的增加習題數(shù)量，這樣不僅給學生帶來了巨大的學習壓力，也不利于教學質(zhì)量的提升，反而引起學生的逆反心理。在習題的選擇上，應(yīng)該加強其綜合性和多維性。從而讓學生將相關(guān)的知識點融合起來，提高對知識點的提煉能力。比如講函數(shù)題、數(shù)例題以及解析幾何等知識要點融合進一道習題中，學生在尋找解題思路的時候，需要調(diào)動之前所學的相關(guān)內(nèi)容，并將有用的點提取出來。多維性是指習題應(yīng)該有多種表現(xiàn)形式，而不是單一的閱讀型習題或者操作性習題。需要注意的是，老師在組織習題內(nèi)容時，必須和書本上的內(nèi)容緊密結(jié)合，不能夠過度脫離課本，讓學生以不同的方式來掌握知識點并進一步提升解題策略。教學案例：已知水渠在過水斷面面積為定值的情況下，過水濕周越小，其流量就越大。現(xiàn)在有以下兩種設(shè)計方式，如圖：

其中，左邊圖的過水斷面是等腰三角形ABC，邊長AB等于邊長BC，過水濕周L1=AB+BC；右邊圖的過水斷面為等腰梯形ABCD，邊長AB=邊長CD，過水濕周L2=AB+BC+CD，如果等腰三角形ABC和等腰梯形ABCD的面積都是S，那么求L1和L2的最小值，并在流量最大的情況下給出最為合理的設(shè)計方案。

這道習題是非常典型的函數(shù)最值問題，可是它的表述方式卻是以平面幾何形式來進行描述的，不僅考查了學生的思維轉(zhuǎn)換能力，還同時考查了對函數(shù)和不等式的實際應(yīng)用能力。在該題的解答過程中，學生能夠?qū)⒑瘮?shù)知識和平面幾何進行有機聯(lián)系，經(jīng)常進行類似習題的聯(lián)系，可以提升其多向性思維能力以及知識整合能力。

3、利用現(xiàn)代化教學手段。通過調(diào)查發(fā)現(xiàn)，很多學生都認為數(shù)學課堂比較枯燥，自己根本提不起學期興趣，這一方面是和數(shù)學自身的性質(zhì)有關(guān)，另一方面也說明目前的數(shù)學教學手段比較落后。多媒體網(wǎng)絡(luò)技術(shù)在當前的語文和英語教學中已經(jīng)應(yīng)用的比較成熟和廣泛，并且得到了非常良好的應(yīng)用效果。但是很多數(shù)學老師，仍然認為在數(shù)學教學中完美沒有必要過多的使用多媒體。尤其是在習題教學中，多媒體技術(shù)根本沒有用武之地，這種想法極大的限制了數(shù)學教學質(zhì)量的提高以及學生學習興趣的提升。實踐證明，多媒體技術(shù)能夠讓數(shù)學習題呈現(xiàn)出更加直觀形象的表達方式，并激發(fā)學生的學習興趣，營造更加良好的學習氛圍。比如，在立體幾何的習題教學中，學生對于抽象的幾何圖像感到非常難以理解，可以利用網(wǎng)絡(luò)上提供的三維模型為學生進行展示，從而讓學生對其中點線面之間的關(guān)系有更加準確的把握[3]。

三、結(jié)論

通過以上分析可以發(fā)現(xiàn)，在目前的高中數(shù)學習題教學過程中仍然存在著很多問題，阻礙了教學質(zhì)量的提升和學生學習興趣的提高，在后期的教學中，老師必須提高對習題教學的正確認識，反思以往的教學弊端，從而制定更加有針對性的教學方案，深化教學方法，提升學生的綜合數(shù)學能力。

參考文獻：

[1] 蘇東貴.高中數(shù)學教學中習題教學的反思[J].讀寫算，2014，（03）：206.

[2] 吳生才.高中數(shù)學教學中習題教學的優(yōu)化策略分析[J].新課程學習，2013，（09）：93.

[3] 侯福艷.關(guān)于高中數(shù)學教學中習題教學的探究[J].中學生數(shù)理化，2014，（04）：99.