數形結合思想在初中數學教學中的滲透探究

陳玉華

摘 要： 在初中數學教學中，教師要關注學生數學思維的培養，在這個時期奠定學生數學思維基礎，對學生未來數學學習有著至關重要的作用。本文以數形結合思維在初中數學教學中的滲透和應用展開研究，希望對我國初中數學教育的創新發展有所助力。

關鍵詞： 初中數學 數形結合 思維方法

引言

數形結合是一種基本的數學思維方法，掌握了這種思維方法，能幫助學生實現數學概念中數、形之間的有效轉換，幫助學生更好地認識知識、理解知識、應用知識，最終提升數學綜合能力。

一、數形結合思想在初中數學教學中的重要作用

隨著教學改革的不斷深入，數形結合思想在數學教學中越來越普及。教師通過圖形將抽象的數學知識呈獻給學生，在集中學生注意力的同時，增強教學的趣味性與師生的互動性。另外，通過數形結合，激發學生的學習興趣，鍛煉他們的空間集合思維，幫助他們提高數學分析能力。可以說，數形結合思想在初中數學教學中發揮著獨特作用，是現階段我國初中數學中不可缺少的重要教學手段。一方面，數形結合思想能很好地解決函數相關的代數問題與幾何問題，通過觀察圖像與模型，幫助學生解決很多應用型問題。另一方面，數形結合思維可以利用幾何圖形、函數的方法解決很多數學方程式問題，有助于求解及函數不等式問題。

二、數形結合的教學實例在初中數學中的應用

在我國初中數學教學中，數形結合是比較常見的教學方法，優勢是將抽象的知識直觀化，培養學生數與形相結合的意識，幫助學生更好地運用數學知識解決實際問題。

（一）以數化形

數學圖形的最大特點就是形象、直觀，很多抽象的數學知識，通過以數化形的方法都能順利、正確地解決。從教學活動方面來看，以數化形可以將抽象的數學知識轉化為直觀的幾何形象，可以減少很多多余環節，幫助學生構建數學思維，使其依托于直觀的數學圖形，結合很多復雜的代數問題，達到良好教學中效果。

比如：“平方差公式”的教學，教師可以利用以數化形的方法開展教學。首先，教師給出一個多項式：（2x+1）（2x-1）；（m+2）（m-2）。先讓學生觀察多項式，之后要求學生運用多項式的原則，展開計算，并將計算結果進行比較，研究其中規律。之后過渡到多項式（a+b）（a-b）的計算，之后自然引出平方差公式，并講解相關基本內容。在這個基礎上，教師通過繪制幾何圖形，對平方差公式進行講解，讓學生體會平方差公式的幾何意義，強化記憶。

（二）以形變數

以形變數是數形結合方法的一種，特點是幫助學生發現圖形中隱含的條件，并借助條件解決很多圖形問題。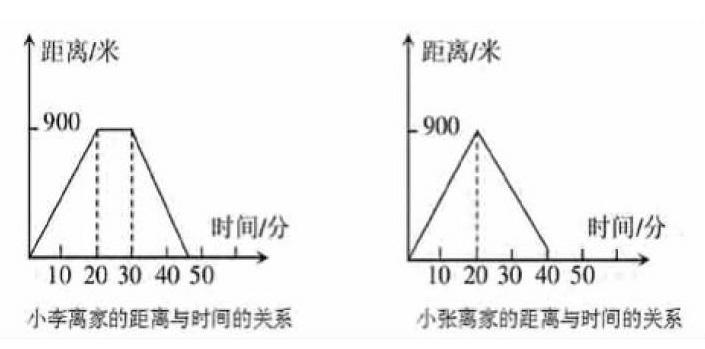

比如：教學“對角平分線的性質”知識點時，先看教材，教材先介紹了平分角的儀器，之后對平分角的儀器工作原理進行了研究，最后引導學生單獨使用尺規作出已知平分角。引入以形變數的思維之后，教師可以先讓學生動手做一做、裁一裁。學生在草紙上，裁剪下一部分，折疊成一個角AOB，之后要求學生仔細觀察自己的操作中出現幾條折疊痕跡，這些折痕的長度優勢多少。通過這樣的方式，教師不僅為學生提供足夠的動手機會，為學生搭建獨立學習探究的平臺，同時加強師生互動，提升教學效率。

（三）數形互變

初中數學教學中，除了單純的“以數化形”及“以形變數”外，還有很多實際數形轉化問題。教學“平面直角坐標系列與函數關系”時，平面直角坐標除了表示地理位置之外，還可以為數與形建立有機聯系，坐標上每個平面的點都有序對應著一個實數，平面上的某一點有X表示，而其對應的實數則用y表示。將圖像與函數建立起直觀又直接的聯系。在應用直角坐標之后，借用代數方法解釋很多幾何現象，選擇幾何方法對代數關系進行分析。

比如：小張和小李是一對從小長到大的好姐妹，在一次周末的時候她們倆約好一起出去游玩。小張和小李從家里出發，走了20分鐘之后來到了一個離家900米的橋邊，這時小張想在橋邊玩，于是開始以原速返回家中，而小李在橋邊玩了10分鐘后，想起自己的作業還沒做完，于是用了15分鐘返回家。試問，你可以在下面的平而直角坐標系中畫出表示小張和小李離家的時間和距離之間的關系嗎？利用數形互變的方法解決，畫出坐標圖，如下圖所示。

這道例題是初中階段數學較為基礎的，也是較為常見的，同時也是我們生活中經常會遇到的問題。面對這樣的問題，教師應該引導學生結合實際問題思考，應用數形結合思想解決這樣的問題，根據題目中給出的信息，我們可以用兩個未知數分別表示時間和距離，這樣就可以解決他們之間的關系，通過這類題型練習，學生對數軸的認識不斷加深，為后面學習奠定基礎。

結語

數學教學中經常應用數形結合思維，如函數、幾何等方面的計算，利用數形結合思維，直觀而準確地解答出答案，同時激發學生對數學知識的興趣，活躍學生課堂思維。當然，教師本身應該具備這種思想，促進教師的教學思維創新，幫助教師具有更開闊的教學視野，初中數學教學中數形結合的應用是我國教育進步的重要表現。

參考文獻：

[1]宗穎.數形結合思想在初中數學教學中的應用[J].環球市場信息導報，2016（18）.

[2]吳僑敏.數形結合思想在初中數學教學中的滲透研究[J].中學教學參考，2016（23）.

[3]梁永娥.數形結合思想在函數問題中的應用[J].中學教學參考，2016（23）.

[4]顧恩，鄒燕.數形結合思想在化學解題中的應用[J].高中數理化，2016（16）.