“數(shù)學(xué)思想”在教學(xué)中的演繹
朱興安
[摘 要]“數(shù)學(xué)思想”是人們在對數(shù)學(xué)長期認(rèn)知探索的過程中獲取的精華,是提高學(xué)生數(shù)學(xué)能力和思維品質(zhì)的核心理論。教師可以從符號思想、類比思想、建模思想三個方面著手,選擇適應(yīng)小學(xué)生年齡特點的教學(xué)內(nèi)容,深入淺出、寓教于樂地讓學(xué)生主動參與、自主探究,切實提高學(xué)生對數(shù)學(xué)思想的領(lǐng)悟,有效提升學(xué)生的數(shù)學(xué)文化素養(yǎng)。
[關(guān)鍵詞]小學(xué)數(shù)學(xué) 符號思想 類比思想 建模思想 演繹
[中圖分類號] G623.5 [文獻(xiàn)標(biāo)識碼] A [文章編號] 1007-9068(2016)35-084
在小學(xué)數(shù)學(xué)教學(xué)中滲透數(shù)學(xué)思想,有利于學(xué)生對數(shù)學(xué)概念、公式、定理的深入理解和靈活運(yùn)用,有利于學(xué)生掌握符號思想、類比思想、建模思想等諸多數(shù)學(xué)思想,實現(xiàn)從知識的傳授到能力的培養(yǎng),使學(xué)生在掌握知識的基礎(chǔ)上學(xué)會分析問題、解決問題,是貫徹課程教學(xué)理念,提升學(xué)生數(shù)學(xué)素養(yǎng)的重要途徑。
一、符號思想,具體情境中總結(jié)規(guī)律
數(shù)學(xué)就是符號加邏輯,其中符號包括字母、數(shù)字、圖形和各種特定的符號,它為數(shù)學(xué)思想的交流提供了便利,消除了語言的障礙。學(xué)生的符號感可以幫助其快速從具體情境中找出數(shù)量關(guān)系和變化規(guī)律,并利用符號簡潔、準(zhǔn)確地表達(dá)出來,有效避免了語言上的含糊性和歧義性,進(jìn)而通過符號之間的轉(zhuǎn)化實現(xiàn)對問題的解決。
比如,在教學(xué)“乘法分配律”時,教師可以建立一定的問題情境,讓學(xué)生討論不同的計算方法,并在解決問題中尋找規(guī)律。教師出示題目:“在服裝店里,一件上衣的價格為175元,一條褲子的價格為75元,買四套這樣的衣服需要多少錢?”學(xué)生通過討論列出(175+75)×4和175×4+75×4兩種算式,這兩種算式都對嗎?學(xué)生積極地進(jìn)行思考、計算,最終認(rèn)為這兩種算式都正確,可以用等號連接,于是便得出了(175+75)×4=175×4+75×4的結(jié)論。在進(jìn)行幾個相關(guān)的練習(xí)之后,學(xué)生掌握了類似算式的計算方法,總結(jié)出(a+b)×c=a×c+b×c。
學(xué)生利用a、b、c來代表不同數(shù)字的方法就是符號思想的體現(xiàn),簡潔、準(zhǔn)確地將數(shù)據(jù)實例集為一體,便于記憶和應(yīng)用。在符號思想的領(lǐng)悟和學(xué)習(xí)中,學(xué)生深刻體會到了符號的實用性和優(yōu)越性。
二、類比思想,對比辨析中遷移知識
“類比思想”是指當(dāng)學(xué)生看到陌生問題中似曾相識的部分時,依據(jù)數(shù)學(xué)對象之間的相似性,將數(shù)學(xué)知識遷移,從而將表面復(fù)雜陌生的問題直接化、簡單化,以幫助學(xué)生打開思路,利用已有的知識經(jīng)驗找出問題的切入點,最終創(chuàng)造性地解決問題。類比思想不是簡單的生搬硬套,需要進(jìn)行一定的抽象分析,這就需要教師的及時點撥和學(xué)生的靈活運(yùn)用。
比如,有這樣一道應(yīng)用題:“星期天小明一家去登山。上山時,每小時行3千米,下山時,每小時行5千米,除去休息和游玩的時間,小明一家上下山花費(fèi)的總時間為5個小時,全程共行了19千米。問上山和下山的路程各是多少千米?”在討論中,不少學(xué)生將這道題看成了一個行程問題,在不用方程的基礎(chǔ)上,學(xué)生較難得出答案。然而,這道題的實質(zhì)是典型的“雞兔同籠”問題的變化,可以這樣來解決:假設(shè)上山時間為5小時,則小明一家所走的路程為3×5=15(千米),比實際行程少了19-15=4(千米),這是因為把下山的時間當(dāng)做了上山的時間,故下山所用的時間為4÷(5-3)=2(小時),從而可以得到上山路程為3×(5-2)=9(千米),下山路程為5×2=10(千米)。
數(shù)學(xué)中還有許多定理都是類比思想的直接反映,如長方形面積與三角形面積、圓柱體積與圓錐體積等,只要學(xué)生領(lǐng)悟了蘊(yùn)含在其中的類比思想,對公式的記憶就更為扎實和準(zhǔn)確,更能激發(fā)學(xué)生的創(chuàng)造力。
三、建模思想,實踐操作中構(gòu)建知網(wǎng)
“建模思想”是人們對數(shù)學(xué)現(xiàn)象的一種概括,利用抽象的數(shù)學(xué)模型來模擬實際生活中的數(shù)學(xué)現(xiàn)象,使學(xué)生學(xué)會如何將實際問題簡化,并將其轉(zhuǎn)化為一個數(shù)學(xué)問題,進(jìn)而從數(shù)學(xué)的角度來解決。建模思想的融入提升了學(xué)生的應(yīng)用意識與實踐能力,促進(jìn)了學(xué)生對數(shù)學(xué)知識與技能的綜合運(yùn)用,能夠使學(xué)生快速找出知識之間的連接點,形成科學(xué)致密的知識網(wǎng)絡(luò)。
例如,在復(fù)習(xí)“平面圖形面積”時,教師可以讓學(xué)生計算教室內(nèi)存在的平面圖形的面積,從而建立一個平面求積的數(shù)學(xué)模型。在對教室的觀察中,學(xué)生需要求出長方形、正方形、三角形、梯形、圓形的面積,通過相互之間的討論,學(xué)生逐步掌握了這些圖形面積的求法,并以長方形為基礎(chǔ)建立了數(shù)學(xué)模型。(如下圖所示)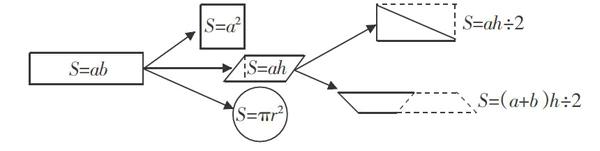
通過對平面圖形的探索,學(xué)生經(jīng)歷了“問題情境—模型構(gòu)建—分類求解—實際應(yīng)用”四個過程,改變了單一的記憶、接受和模仿的學(xué)習(xí)方法,有效促進(jìn)學(xué)生參與實踐、思考探究,真實了解了建模思想。
當(dāng)然,數(shù)學(xué)思想在小學(xué)數(shù)學(xué)教學(xué)中的滲透,不僅僅是要培養(yǎng)學(xué)生的思維能力,也要注重對其情感素養(yǎng)的熏陶,強(qiáng)調(diào)在學(xué)習(xí)知識、技能和方法的同時,注重學(xué)生情感的積極體驗,激發(fā)學(xué)生平穩(wěn)、持續(xù)的學(xué)習(xí)動力。
(責(zé)編 李琪琦)

