巧妙運(yùn)用運(yùn)動疊加原理解題
張冬英
【摘要】本文巧妙運(yùn)用運(yùn)動的疊加原理,將重力加速度分解為沿斜面方向和垂直斜面方向的兩個分量、將小球的分段式斜拋運(yùn)動沿斜面向下和垂直斜面向上兩個方向分解,從而使小球的空間復(fù)雜運(yùn)動得到簡化,即沿斜面方向小球作勻加速直線運(yùn)動,垂直斜面方向,小球作周期性的類豎直上拋運(yùn)動,這樣問題便迎刃而解。
【關(guān)鍵詞】巧妙運(yùn)用 運(yùn)動疊加原理 分解重力加速度
【中圖分類號】G633.7 【文獻(xiàn)標(biāo)識碼】A 【文章編號】2095-3089(2017)01-0101-01
【原理】一個運(yùn)動可以分解成幾個同時進(jìn)行的且相互獨(dú)立的分運(yùn)動的疊加,這就是運(yùn)動的疊加原理,又叫運(yùn)動的相對性原理。
【題目】①彈性小球從高h(yuǎn)處自由落下,落到與水平面成θ角的長斜面上,碰撞后以同樣大小的速率反彈回來。1.求每個彈回點(diǎn)(第一個點(diǎn)和第二個點(diǎn),第二個點(diǎn)和第三個點(diǎn),…第n個點(diǎn)和第n+1個點(diǎn))間的距離x1,x2, …,xn。2.求當(dāng)斜面以勻速度u沿豎直方向向上運(yùn)動時的x1的數(shù)值。
【分析】小球每次與斜面碰撞后,都將作不同初速度的斜拋遠(yuǎn)動,而對斜拋運(yùn)動的處理,根據(jù)運(yùn)動的疊加原理,常規(guī)的方法是將其分解成水平方向的勻速直線遠(yuǎn)動和豎直方向的上拋運(yùn)動。如果按此慣例,求解過程極其繁瑣。但仔細(xì)分析會發(fā)現(xiàn),巧妙運(yùn)用運(yùn)動的疊加原理,求解問題會較為容易。
【解答1】斜拋運(yùn)動是加速度恒為g的變速曲線運(yùn)動。撇開慣例,將斜面上的斜拋運(yùn)動分解成垂直斜面向上的上拋運(yùn)動和沿斜面向下的勻加速直線運(yùn)動。
如圖1所示,建立XOY坐標(biāo)系,由小球碰撞后以同樣大小的速率反彈知:小球每次與斜面碰撞前后,X軸方向的分速度大小、方向均不變,Y軸方向的分速度大小不變、方向相反;小球的整個運(yùn)動過程等效為:
Y軸方向是不斷重復(fù)進(jìn)行的等時上拋運(yùn)動,上拋初速度均為vyo=vCosθ、上拋加速度恒為ay=-gCosθ。
任意兩相鄰彈回點(diǎn)之間,小球的運(yùn)動時間均為Y軸方向的一次上拋下落的時間,即:
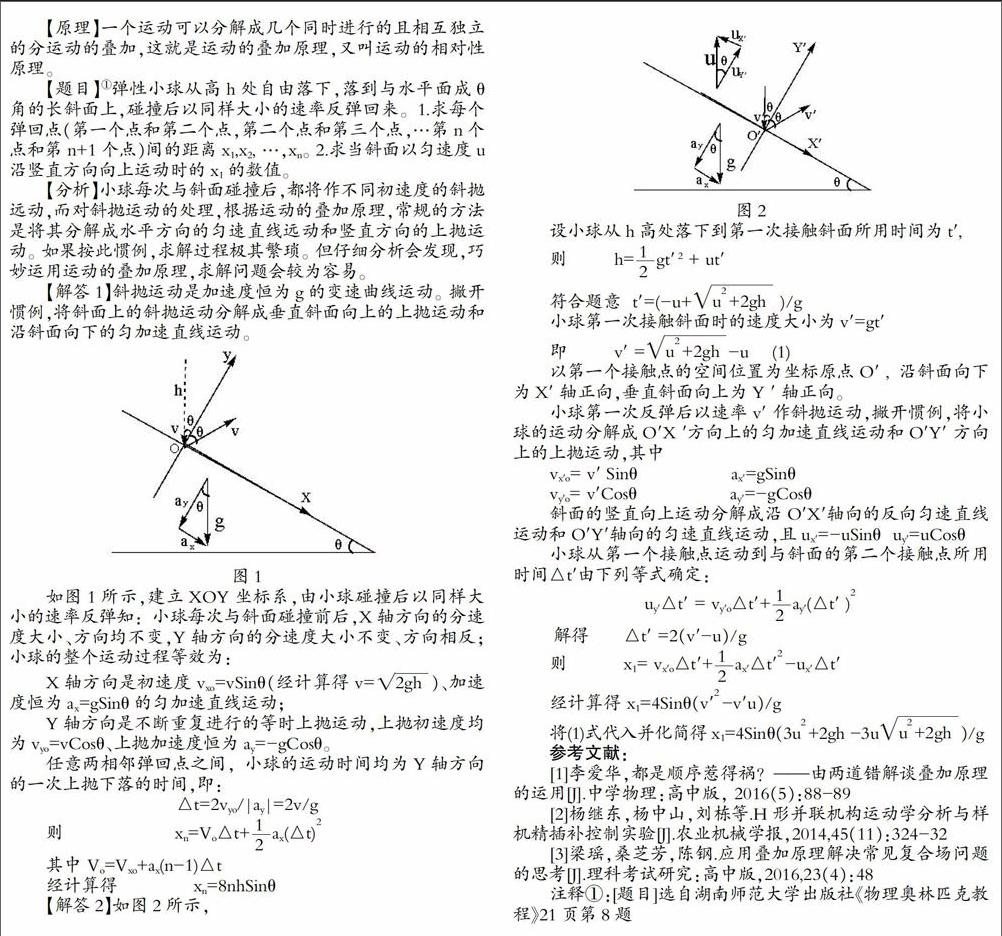
【解答2】如圖2所示,
以第一個接觸點(diǎn)的空間位置為坐標(biāo)原點(diǎn)O′ ,沿斜面向下為X′ 軸正向,垂直斜面向上為Y ′ 軸正向。
小球第一次反彈后以速率v′ 作斜拋運(yùn)動,撇開慣例,將小球的運(yùn)動分解成O′X ′方向上的勻加速直線運(yùn)動和O′Y′ 方向上的上拋運(yùn)動,其中
vx′o= v′ Sinθ ax′=gSinθ
vy′o= v′Cosθ ay′=-gCosθ
斜面的豎直向上運(yùn)動分解成沿O′X′軸向的反向勻速直線運(yùn)動和O′Y′軸向的勻速直線運(yùn)動,且ux′=-uSinθ uy′=uCosθ
小球從第一個接觸點(diǎn)運(yùn)動到與斜面的第二個接觸點(diǎn)所用時間△t′由下列等式確定:
參考文獻(xiàn):
[1]李愛華,都是順序惹得禍?——由兩道錯解談疊加原理的運(yùn)用[J].中學(xué)物理:高中版, 2016(5):88-89
[2]楊繼東,楊中山,劉棟等.H形并聯(lián)機(jī)構(gòu)運(yùn)動學(xué)分析與樣機(jī)精插補(bǔ)控制實(shí)驗(yàn)[J].農(nóng)業(yè)機(jī)械學(xué)報,2014,45(11):324-32
[3]梁瑤,桑芝芳,陳鋼.應(yīng)用疊加原理解決常見復(fù)合場問題的思考[J].理科考試研究:高中版,2016,23(4):48
注釋①:[題目]選自湖南師范大學(xué)出版社《物理奧林匹克教程》21頁第8題

