如何在高中數學教學中滲透數學思想

敬林森

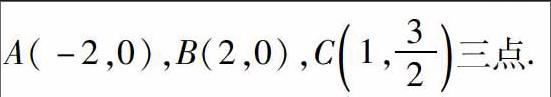
【摘要】數學思想是隱藏在數學知識體系中的無形知識，教師要通過解題向學生滲透這種思想，使學生可以在探究中形成自己的思維方式，逐步地掌握數學思想.本文主要探究了轉化、分類討論和數形結合思想的應用，以期提高學生的數學思維能力.

【關鍵詞】高中數學；數學思想；轉化；數形結合；分類討論

常見的數學思想有轉化、分類討論和數形結合，教師要引導學生做題時多看、多想、多畫，重視學生的空間想象能力、邏輯思維能力、化歸轉化能力的提高.為了提高學生的數學思想意識，教師要在教學過程中點明數學思想；在試卷分析中滲透數學思想；在實踐練習中運用數學思想，在無形中使數學思想可以融入學生的思維中，在潤物細無聲中提高學生的思維能力，掌握數學思想.

一、轉化思想，轉未知為已知

轉化思想顧名思義就是把數學試題中的概念、公式或數量進行轉化，通過已知條件和數據來求未知的數據.有些題目看似與所給條件沒有任何關系，但是通過轉化就會發現，所給條件正是求出未知數據的關鍵，只要注重使用轉化思想就可以.學生要明確其中隱藏的知識規律，靈活轉化，找到所給條件之間的聯系，進而利用已知條件解決未知問題.例如，已知橢圓E的中心在坐標原點，焦點在坐標軸上，且經過

（Ⅰ）求橢圓E的方程；

（Ⅱ）若點D為橢圓E上不同于A，B的任意一點，F（-1，0），H（1，0），當△DFH內切圓的面積最大時，求△DFH內心的坐標.

解決第一問時，學生可以根據橢圓經過A，B，C三點，設方程為mx2+ny2=1，得到m，n的方程組，解出m，n得到橢圓方程；在解決第二問時，學生可以將△DFH內切圓的面積最大，轉化為△DFH的面積最大，進而轉化為點D的縱坐標的絕對值最大，此時D為橢圓短軸端點.這種轉化的思想會讓學生發現問題變得簡單了很多，從而可以找到解題思路，在轉化思想的引導下順利地解題.計算中，學生會看到 ，

二、分類討論，全面考慮問題

分類討論是數學學習中的一種重要思想，二次函數、一元二次方程及一元二次不等式的綜合應用，以及冪函數的圖像及性質，都會涉及分類討論思想.教師要引導學生全面地看問題，對知識分幾種情況進行討論，而不是單一地看問題.例如，試題：已知f（x）=x2+3x-5，x∈[t，t+1]，若f（x）的最小值為h（t），寫出h（t）的表達式.解題中學生需注意：如圖所示，函數圖像的對稱軸為x=-32，學生需要分幾種情況來分別討論，才能夠完整地解決問題.

本題中對稱軸的位置相對于區間的位置不同，就會有不同的答案.學生在分析中要把各種可能性都考慮到，同時還要對此類問題進行歸納總結，探究一般規律.學生要認識到在研究有關二次函數最值時，一般用分類討論思想，一是對系數a進行討論，二是要對對稱軸進行討論，在分類討論中要遵循分類的原則：一是分類的標準要一致；二是分類時要做到不重不漏；三是能不分類的要盡量避免分類，絕不無原則地分類討論.通過歸納，學生會更好地理解分類討論的數學思想，進而在解題過程中靈活地應用.

三、數形結合，直觀形象生動

數形結合會幫助學生更好地理解抽象的數學知識，變抽象為形象具體.在高中數學知識學習過程中，學生會發現函數知識、平面幾何、立體幾何、雙曲線等等數學問題都可以采用數形結合的思想來解決問題.一邊讀題，一變化圖，根據已知條件來繪圖，簡單直觀地看到數量關系，可以更迅速快捷地解題.

總之，教師應對學生進行“授之以漁”的教學，多向學生傳授數學思想和方法，引導學生學會分析數學知識規律，進而在解題過程中靈活地應用.教學中教師要善于結合試題，向學生滲透數學思想，使學生可以利用數學思想來順利地解決問題，提高能力.