見微知著，優(yōu)化教學(xué)

肖雄偉

[摘 要] 教學(xué)的過程是從未知向已知不斷生成的過程，生成不可一蹴而就，而應(yīng)該關(guān)注于“微”處，通過細(xì)微處教學(xué)的精細(xì)化實(shí)現(xiàn)課堂教學(xué)的有效、高效.

[關(guān)鍵詞] 高中數(shù)學(xué)；微；教學(xué)；目標(biāo)；問題

教學(xué)的過程是動(dòng)態(tài)生成的過程，早在1974年，美國(guó)的心理學(xué)家維特洛克發(fā)表了《作為生成過程的學(xué)習(xí)》一文，文章把“生成學(xué)習(xí)”作為一個(gè)觀點(diǎn)做了明確表態(tài)，并且從心理學(xué)的角度論述了“生成”這一概念，隨著當(dāng)前新課程改革的深化，“生成性教學(xué)”被越來越多地提起，對(duì)于高中數(shù)學(xué)教學(xué)，如何借助于生成性教學(xué)模式促進(jìn)教學(xué)效果的提升呢？筆者認(rèn)為應(yīng)該抓住一個(gè)“微”字，教學(xué)環(huán)節(jié)的“微化”、教學(xué)目標(biāo)的“微化”、問題的“微化”、思路的“微變”等等，見微知著促進(jìn)知識(shí)、方法、能力的生成.

[?] 微化環(huán)節(jié)，提高課堂效率

教學(xué)是復(fù)雜的過程，如何提升課堂效率呢？筆者認(rèn)為需要我們教師在教學(xué)設(shè)計(jì)的過程中結(jié)合教材的特點(diǎn)和學(xué)生的具體學(xué)情進(jìn)行精致化的處理，將一整節(jié)課進(jìn)行“微化”和拆解，讓我們每一個(gè)教學(xué)環(huán)節(jié)都能夠貼合學(xué)生的具體學(xué)情，實(shí)現(xiàn)因材施教.

例如，“函數(shù)概念”這節(jié)課，筆者在教學(xué)環(huán)節(jié)的設(shè)計(jì)上進(jìn)行了如下的“微化”.

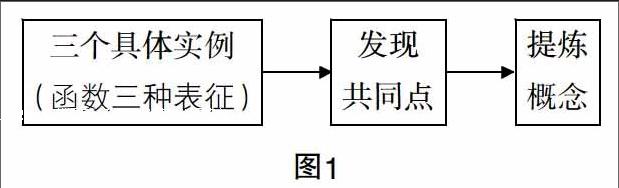
從教材設(shè)計(jì)來看，粗線條地分割課堂環(huán)節(jié)，可以將一整節(jié)課分層如下3個(gè)模塊（如圖1所示）.

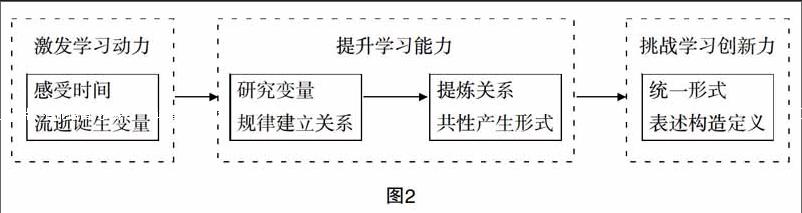
這樣的設(shè)計(jì)看上去毫無問題，但是實(shí)際教學(xué)中卻不是很理想，為什么？?jī)H僅給學(xué)生提供幾個(gè)生活中的實(shí)例，學(xué)生很難發(fā)現(xiàn)其中存在的共同點(diǎn)，提煉和抽象出概念就更困難了. 為什么？因?yàn)榻滩牡木幣艑?duì)學(xué)生而言存在著較大的知識(shí)與思維跨度，怎么辦？必須合理地調(diào)整教材教學(xué)內(nèi)容的順序，同時(shí)將教學(xué)環(huán)節(jié)“微（觀）化”，使其符合學(xué)生的學(xué)習(xí)心理特征，提高課堂教學(xué)的實(shí)效，筆者對(duì)于這節(jié)課的教學(xué)環(huán)節(jié)進(jìn)行了如下的設(shè)計(jì).

站在數(shù)學(xué)知識(shí)的系統(tǒng)性角度來看，聯(lián)系函數(shù)三種表征的核心是“變量”，學(xué)生對(duì)變量是有認(rèn)知基礎(chǔ)的，但是認(rèn)識(shí)存在片面性，我們?cè)诮虒W(xué)之初就應(yīng)該讓學(xué)生清楚地意識(shí)到其在函數(shù)中所扮演的角色，為此在教學(xué)環(huán)節(jié)的設(shè)計(jì)上選擇了從“了解變量”入手，以此為基礎(chǔ)將“函數(shù)”的三個(gè)表征進(jìn)行有效的串接，最終統(tǒng)一表述概括為可以揭示函數(shù)本質(zhì)的定義.

實(shí)踐經(jīng)驗(yàn)表明，我們要想提升課堂教學(xué)的效率，就必須結(jié)合學(xué)生的學(xué)齡特點(diǎn)將我們教學(xué)的每一個(gè)環(huán)節(jié)做到精細(xì)，確保學(xué)生每個(gè)環(huán)節(jié)的情感體驗(yàn)都是正向和積極的，都能將原有的認(rèn)知經(jīng)驗(yàn)和新問題的解決聯(lián)系到一起.

[?] 微化目標(biāo)，明確重、難點(diǎn)

“目標(biāo)來源于并運(yùn)行于活動(dòng)之中……是活動(dòng)中而非活動(dòng)的轉(zhuǎn)折點(diǎn)”這個(gè)觀點(diǎn)得到了諸多教育學(xué)家的肯定. 新課程改革以來，我們大家對(duì)“教學(xué)目標(biāo)”有了新的認(rèn)識(shí)，教學(xué)目標(biāo)不應(yīng)該是單一性的，它是教師與學(xué)生在知識(shí)的平臺(tái)上互動(dòng)交流、切磋學(xué)習(xí)產(chǎn)生的一個(gè)豐滿的體系，具有豐富的層面以及各個(gè)層面的不斷擴(kuò)展、延伸. 因此，在這樣的理論引導(dǎo)下，初期教學(xué)的策劃、目標(biāo)的樹立本身就應(yīng)該設(shè)立為明確的“微化目標(biāo)”，借助于對(duì)教學(xué)目標(biāo)的微化，將真正的重、難點(diǎn)凸顯出來，提高課堂教學(xué)和探究方向的明確性.

例如，關(guān)于“函數(shù)單調(diào)性”的教學(xué)，從教學(xué)重、難點(diǎn)上看，本節(jié)課主要目標(biāo)是要引導(dǎo)學(xué)生發(fā)現(xiàn)如何運(yùn)用多個(gè)維度的數(shù)學(xué)語言對(duì)“函數(shù)單調(diào)性的定義”進(jìn)行有效的描述和表征，讓學(xué)生充分體驗(yàn)對(duì)函數(shù)單調(diào)性的定義進(jìn)行描述的過程. 既然確立了這樣一個(gè)目標(biāo)，那么我們?cè)诮虒W(xué)過程中就應(yīng)該向著這個(gè)目標(biāo)努力，課前我們應(yīng)該有這樣的思考：如果進(jìn)一步微化重、難點(diǎn)，數(shù)學(xué)語言又可以從圖形、文字、符號(hào)三個(gè)方面進(jìn)行，難在哪里呢？圖形、文字都不難，但是都僅僅是定性的描述，顯然是不夠準(zhǔn)確的，因此通過目標(biāo)的微化，本節(jié)課的教學(xué)目標(biāo)就被鎖定在了如何運(yùn)用“符號(hào)語言”來定量地刻畫函數(shù)單調(diào)性這個(gè)問題上.

[?] 微變問題，促進(jìn)生成

數(shù)學(xué)知識(shí)和方法的生成是一個(gè)復(fù)雜而漫長(zhǎng)的過程，如果我們不注重問題設(shè)計(jì)的精細(xì)化，難以給學(xué)生留下深刻的印象，問題微型化、微變化能夠深刻刻畫數(shù)學(xué)概念，提高學(xué)生對(duì)數(shù)學(xué)知識(shí)的理解程度.

仍然以“函數(shù)單調(diào)性”的教學(xué)為例，為了促進(jìn)學(xué)生運(yùn)用數(shù)學(xué)符號(hào)來表征和刻畫數(shù)學(xué)概念，筆者在問題設(shè)計(jì)的細(xì)微處進(jìn)行多次微變與追問.

問題1：是否可以由1<2<3<…<99<100時(shí)f（1）

引導(dǎo)學(xué)生從作圖的角度進(jìn)行問題解決的推演，將符號(hào)語言與圖像語言相結(jié)合，但是學(xué)生的認(rèn)識(shí)往往還停留在定性的層面，如何促進(jìn)認(rèn)識(shí)的深入呢？可以將問題微變.

問題2：如果f（2）

問題2的設(shè)計(jì)是為了讓學(xué)生接近準(zhǔn)確的數(shù)學(xué)語言表述，但是不要急于給學(xué)生下定義，而是讓學(xué)生充分地體驗(yàn)“任意”二字，在學(xué)生認(rèn)識(shí)形成后，可以將認(rèn)識(shí)與函數(shù)圖像的幾何意義相結(jié)合，結(jié)合幾何意義（借助于圖像在區(qū)間內(nèi)任意兩點(diǎn)連線斜率的正、負(fù)來分析），進(jìn)行比較，當(dāng)然對(duì)于初學(xué)者而言，要想很好地理解單調(diào)性還是有難度的，等學(xué)習(xí)了導(dǎo)數(shù)后就可以深入概念的數(shù)學(xué)本質(zhì).在得到定義后，還可以對(duì)定義進(jìn)一步探究.

[?] 微變思路，發(fā)散思維

最終數(shù)學(xué)學(xué)習(xí)的效果是通過解決問題來反饋的，而很多學(xué)生反映課堂上能聽懂，做題時(shí)總是思路理不順，其根本原因在于學(xué)生的思維沒有被有效打開，容易出現(xiàn)思維定式或“漏洞”. 為了促進(jìn)學(xué)生思維發(fā)展，我們?cè)诮虒W(xué)過程中一定不能滿足于問題的解決，還應(yīng)該關(guān)注于解題思路的微變與拓展.

例1：如圖3所示的長(zhǎng)方體ABCD-A1B1C1D1中，E為BC的中點(diǎn)，求證：BD1∥平面DEC1.

思路1：從解題的思路上來看，很多教師和學(xué)生滿足于“中心投影”法：BD1∥OE（O=DC1∩CD1，構(gòu)建三角形中位線），如果我們教師在這個(gè)問題的解決中只滿足于運(yùn)用這個(gè)思路來完成例1的解答，那么不利于思維的發(fā)散，除了這個(gè)思路還有其他的思路么？給學(xué)生足夠多的時(shí)間，學(xué)生就會(huì)將思維的方向進(jìn)行拓展與延伸.

如何轉(zhuǎn)化可以證明線面平行？稍加停頓，學(xué)生就很自然地聯(lián)系到“線線平行”或“面面平行”，思路也就隨之而來.

思路2（平行投影法）：具體的思維方向有2個(gè)：（1）BD1∥DG（G=B1B∩C1E）；（2）BD1∥C1H（H=AB∩DE）.

思路3（轉(zhuǎn)換法）：設(shè)E1為B1C1的中點(diǎn)，從平面DEC1與平面BE1D1之間存在的位置關(guān)系入手，將線面平行問題轉(zhuǎn)化為面面平行問題.

思路4（向量法）：（1）借助于“基底”進(jìn)行推證；（2）借助于空間直角坐標(biāo)進(jìn)行算證.

當(dāng)然，也并非所有的數(shù)學(xué)問題都能聯(lián)系到多種解決問題的方法，但是這種有意識(shí)地拓寬解決問題思路的做法值得我們每一個(gè)數(shù)學(xué)老師在教學(xué)過程中進(jìn)行嘗試，因?yàn)槲覀兘處熡幸庾R(shí)地拓展思路會(huì)對(duì)學(xué)生有潛移默化的影響，長(zhǎng)期的浸潤(rùn)有助于學(xué)生科學(xué)素養(yǎng)和發(fā)散性思維的提升.

總之，我們教育的目的最終是發(fā)展學(xué)生的綜合素養(yǎng)，對(duì)于高中數(shù)學(xué)而言要發(fā)展學(xué)生的理解力、創(chuàng)造力、情感、態(tài)度等等諸多方面，因此教學(xué)環(huán)節(jié)、問題和思路的引導(dǎo)不可過于粗獷，多從“微”處著手與展開，順應(yīng)素質(zhì)教育的要求，長(zhǎng)期下來，有助于提升學(xué)生思維的縝密性和創(chuàng)新性，甚至于有些是我們教師所沒有想到的新的觀點(diǎn)、新的認(rèn)知，這些生成顯然不是學(xué)生死記硬背的結(jié)果，而是“微”教學(xué)的成果. 我們把每個(gè)細(xì)微之處做實(shí)了，在借助于運(yùn)用、拓展、串聯(lián)等方式將學(xué)習(xí)的成果進(jìn)行整合最終獲得的將是更為穩(wěn)固的知識(shí)與能力.