初中數學教學中數形結合思想的應用分析

吳永燕

【摘要】在初中數學教學活動中，數形結合思想是一種科學合理的教學思維。對于學生來說，數形結合思想也是極為有效的解題思路。文章就數形結合思想的重要意義與作用進行了闡述，探討了初中數學教學活動中數形結合思想的應用策略，旨在幫助初中數學教師充分意識到數形結合思想的重要性，并在教學活動中加以靈活應用。

【關鍵詞】初中數學；數形結合；以數化形；以形變數；數形互換

一、前言

在數學學科中，數形結合是極為重要的思維模式，是通過將抽象化的數字與具象化的圖形相互結合來解釋數學知識點與數學問題。在初中數學教學中，對于數形結合思維模式的應用可以簡化數學知識的理解過程，并降低數學題目的解析難度。此外，數形結合思想還是一種知識遷移模式，對于教師來說，數形結合思想的應用可以有效提高教學質量。

二、數形結合思想的重要意義

在各個階段的數學教學中，數形結合思想的有效性與科學性已經被證實，并被廣泛應用于教學實踐當中。通過應用數形結合的思想，教師可以將問題以更加直觀與清晰的圖形形式向學生展示，提高學生的理解能力與理解效率，并激發學生學習數學知識的信心與興趣，幫助學生更好地學習數學。數形結合思想的應用，可以增強初中數學教學活動的趣味性，吸引學生的注意力，提高學生的關注度，能夠同時培養學生的代數思維與結合思維，提高學生的數學分析能力。此外，數形結合思想能夠幫助學生將不同的數學知識有機結合起來，在更好地理解新知識的同時，鞏固以往學過的知識內容。

在初中數學教學中，數形結合思想的重要作用包括以下方面：第一，簡化數學知識內容，降低數學題目的解析難度；第二，有利于學生更好地理解數學題目中的解題條件，更加高效而準確地進行相關題目的解析；第三，幾何圖形與函數圖像的應用可以幫助學生進行方程式的轉化，便于方程題型的解題；第四，在不等式題型的解題過程中，數形結合思想也會起到重要作用。

三、數形結合思想在初中數學教學中的應用

數形結合思想是將抽象化的數字與具象化的圖像進行有機結合與相互轉化的重要方式，通常在闡述與解釋數學概念中的應用較多，對于數學題型的解析也不失為一種有效的方法。具體可以應用于代數與幾何題目當中，能夠降低解析難度，提高學生對于數學概念的理解能力，提高解題效率等，在數學學科中的應用具有較大的優勢。

（一）以數化形

以數化形的思想主要應用在初中數學的代數知識教學中。代數是初中數學的重要內容，給學生的學習帶來一定的困難。學生在學習代數知識并利用代數知識來解答代數題型的時候，常常出現難以理解求解等問題。這時，通過將抽象的代數條件以函數圖像的方式展現出來，就可以幫助學生更加直觀地理解題目中的條件，降低解題難度。同時，利用數形結合的方式，也便于學生理解并記憶代數知識點。

例如，在初中數學教學活動中，可以將一元二次方程看作一種函數，結合函數與代數知識來理解問題，并利用數形結合的方式直觀表示。舉例說明，對于一元二次方程，通過以數化形進行轉換，首先將之轉化為函數式，即，。以函數坐標的形式加以表現，繪制函數拋物線圖形，則拋物線與橫坐標的兩個交點就是該一元二次方程的解。在講解一元二次方程的過程中，教師將數形結合的思想滲透到課堂教學當中，潛移默化地在學生心目中構建數形結合思維，能夠培養學生良好的學習習慣，切實提高初中數學教學質量與教學效果。

諸如二次函數這種將幾何與代數相結合的數學知識點，在教學與學習過程中的難度較大，練習與考試有很大的靈活調整空間，通常在中考中占據了單一題目的最大分值。考慮到二次函數代數與幾何相互融合的特點，教師可充分發揮數形結合這一教學方法的優勢，通過繪制函數圖像展示二次函數變化的過程，提高學生的理解水平，并激發學生的學習欲望，提高學生的數學思維能力。

（二）以形變數

在初中數學教學中，數形結合的思想可以引導學生更好地挖掘圖形中的條件，更加順利地解決圖形問題。例如，在講解三角形的相關知識時，教師可以運用數形結合的思想幫助學生明確圖形之間的關系，深入理解知識內容。

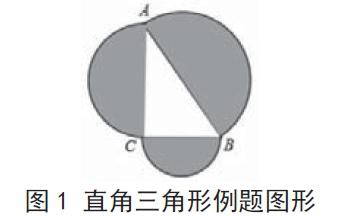
如圖1，某直角三角形三條邊長分別為，，，分別以三條邊長為直徑，畫出三個半圓，求圖中的陰影部分面積。

在分析該題目時，教師可以引導學生畫出圖形，通過圖形可以很清晰地明確三角形與半圓之間的關系，并明確解題方法。題目已經給出了三角形的邊長與半圓的直徑，則可以分別確定三個半圓的面積，最后將其相加即可。在引導學生解題的過程中，教師通過繪制圖形來幫助學生理解題目，能夠厘清解題思路。通過數形結合，教師還可以引導學生鞏固以往學習過的數學知識，培養學生的系統性思維能力。

圖1 直角三角形例題圖形

（三）數形互換

有一些數學問題并不是簡單地通過以數化形或者以形變數就能夠解決的，還需要在充分理解數學題目，明確題目條件的前提下，更加靈活地通過數形互換來解決問題。這就需要教師引導學生充分掌握數形結合的解題思路，幫助學生根據不同情況靈活運用數形結合的方式理解知識點，并靈活解析題目。

例如，在講解“平面直角坐標系與函數”的相關知識點時，教師可以將平面直角坐標系作為數形結合的重要媒介，在平面直角坐標系上對應平面上的點和有序實數，結合函數與圖形知識，從幾何的角度理解代數問題，以代數方式研究幾何性質，向學生更加直觀地展示這一知識點，在學生大腦中構建數形結合的數學思維，幫助學生掌握更加有效的解題方式。

四、結語

教師在運用數形結合思想進行教學的過程中需要對教學材料與教學內容有充分而全面的了解，明確在何種條件下可運用數形結合思想進行教學，并將這一思維模式教授給學生，引導學生靈活運用數形結合的方式理解數學問題，通過提高學生解析數學問題的效率與準確度，幫助學生樹立自信心，增強學生對初中數學的學習興趣。

【參考文獻】

[1]金信凱.數形結合思想教學在初中數學教學中的應用研究[J].才智，2017（02）：99.

[2]嚴志鋒.相互滲透，交叉作用——論初中數學教學中數形結合思想的應用[J].數學大世界（上旬），2016（04）：62.