反例在初中數(shù)學教學中的作用

何艷萍

【摘要】數(shù)學教學中運用反例展開教學可以有效促進學生對概念、定理、公式等的理解和掌握，更直觀地引導學生判斷命題的真假，幫助學生克服思維定式，激發(fā)學生的學習興趣。教師應結合實際選取具有針對性的反例并在課堂教學時選擇恰當時機引入。

【關鍵詞】初中數(shù)學 反例教學 意義與策略

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2018）04A-0125-02

在初中數(shù)學八年級的教學中，學生學習了“命題與證明”這一內容，接觸到了反例這一概念。在數(shù)學教學中，證明在幾何教學中的地位舉足輕重，反例的地位與之不相上下。反例的構建和應用是一種非常重要的教學手段和方式，它有助于培養(yǎng)學生良好的思維品質，激發(fā)學生學習的興趣，幫助學生有效進行知識的整合。如果教師能對反例運用得當，可事半功倍。

一、有效促進學生對概念的理解和掌握

數(shù)學概念是數(shù)學知識的基礎，小學數(shù)學中的概念教學比較生活化、直觀化，而初中概念教學由生活化向抽象化轉換，更具有邏輯性。學生在學習概念時容易出現(xiàn)理解或認識錯誤的現(xiàn)象，要是教師只運用正面的例子來引導學生，學生的理解不夠深刻，若教師在這個時候適當?shù)亓信e反例，從反面消除學生出現(xiàn)的疑惑，從側面抓住概念的本質，彌補正面例子的不足，可以加深學生對概念的理解，讓學生不僅弄清“是什么”，還弄清“不是什么”。

例如，在“有理數(shù)”的概念教學當中，教師可以通過練習“請在下列數(shù)中找出所有的有理數(shù)：-2，[13]，0.56，1.1010010001……（1和1之間每次增加一個0），[1π]”展開概念教學，學生有可能會得出1.1010010001……（1和1之間每次增加一個0）和[1π]也是有理數(shù)的結論，教師可引導學生著重分析“有理數(shù)”的概念“整數(shù)和分數(shù)統(tǒng)稱為有理數(shù)”表達的更具體的含義——分數(shù)可以寫成有限小數(shù)或無限循環(huán)小數(shù)，所以又可以說有理數(shù)包括整數(shù)、有限小數(shù)和無限循環(huán)小數(shù)。1.1010010001……（1和1之間每次增加一個0）和[1π]都是無限的，但是它們是不循環(huán)小數(shù)，所以它們不是有理數(shù)。

再例如，在八年級學到“函數(shù)”概念時，學生認為只要一個變量隨另一個變量變化而變化，就是函數(shù)。教師可以讓學生思考以下問題：“下列變量關系中，說法正確的有哪些：①若[y]=x，則y是x的函數(shù)；②若y=2[x]（x≥0），則y是x的函數(shù)；③水管中水流的速度和水管的長度成函數(shù)關系。”正確的答案是②。說法①：設x=5，[y]=5，y=±5，在函數(shù)關系中，當給定了x的值，y只能有唯一的值與它對應，所以①的說法是錯誤的。說法③：水管中水流的速度不會受到水管的長度的影響，所以它們之間不存在函數(shù)關系。通過恰當?shù)姆蠢瑢W生深刻理解和掌握了所要學習的概念。

二、有效且直觀地判斷真假命題

肯定一個命題的正確性，需要經(jīng)過嚴密的推理和論證，而要推翻一個命題，只需要一個反例即可。一個具體的實例讓學生在矛盾沖突中，更深刻地理解和掌握與命題相關的概念性質。

例如：①如果[a]=[b]，那么a=b。

反例：當a和b互為相反數(shù)，如2和-2時，[2]=[-2]，但2≠-2。

②帶有負號的數(shù)是負數(shù)或-a是負數(shù)。

反例：-0=0，或當a=-5時，-a=-（-5）=5，但0和5都不是負數(shù)。

③相等的角是對頂角。

反例：圖1中互為鄰補角的兩個直角∠ACB=∠ACD，圖2等腰直角三角形ABC中∠A=∠B，但是∠ACB和∠ACD、∠A和∠B都不是對頂角。

④帶根號的數(shù)都是無理數(shù)。

反例：[9]=3，但是3不是無理數(shù)。

⑤如果a2=b2，那么a=b。

反例：（-4）2=42，但是-4≠4。

三、使學生正確掌握數(shù)學定理、公式和性質

學生在學習一個新的定理、公式和性質時，往往會忽視定理、性質中的關鍵詞，不注意使用的條件，只側重記住結論，生搬硬套從而造成解題錯誤。為了改善這一現(xiàn)象，教師可適當引入反例，幫助學生理解與掌握定理和性質。

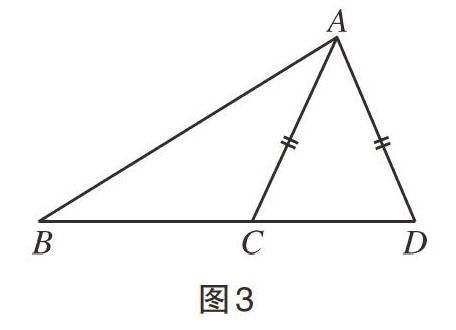
例如，在學習八年級全等三角形的判定方法“兩邊及其夾角分別相等的兩個三角形全等，記為邊角邊或SAS”時，學生往往忽略掉“夾角”這一個判定的關鍵，錯誤地記成“兩邊和一角”即SSA，此時，教師可以出示反例：如圖3，AB=AB，AC=AD，∠ABC=∠ABD，已具備了“兩邊和一角”的條件，但顯然第三邊BC與BD的長度不相等，△ABC和△ABD并不全等。所以在滿足了“兩邊和一角”的條件后，“一角”必須是“兩邊”的“夾角”才可以由“邊角邊”的判定方法得到三角形全等。學生理解了這個定理中夾角的“夾”的深刻含義，達到準確掌握和運用定理的目的。

再例如，學生在運用一次函數(shù)y=kx+b（k≠0）的圖象與性質時會忽略k≠0。教師在教學時可以有針對性地引入這樣一道題：“一次函數(shù)y=（4a-5）x-（2a-2），當a，b為何值時，函數(shù)圖象與y軸的交點在x軸的下方？甲乙兩名學生解答得到不同答案。甲的解答：-（2a-2）<0，解得a>1；乙的解答：4a-5≠0且-（-2a-2）<0，解得a>1且a≠[54]。誰是正確的呢？”學生在經(jīng)過思考和討論后，得出甲錯、乙對的結論，教師此時就可以引導學生仔細觀察，分析發(fā)現(xiàn)甲同學在解題過程中，忽略了一次函數(shù)斜率k≠0的條件，而乙同學在解題過程中考慮到了k≠0的條件。通過這一反例，教師引導學生從本質上理解如何正確運用定理與性質，學生認識到在實際解題過程中，必須要全面考慮滿足定理、性質所需要的條件，注意當中的關鍵詞，按要求去做。

四、有效克服思維定式

學生在學習過程中容易產(chǎn)生思維定式，反例的應用能夠有效解決此問題。例如，在學習了勾股定理后，學生把“勾3、股4、弦5”念成了順口溜，他們只要看到一個直角三角形的兩邊的長分別是3和4，就得到第三邊的長為5，此時就有必要舉出反例了：當邊長為4的邊不是直角邊而是斜邊時，第三邊的長為[7]。這樣一來，學生就會從多個角度去考慮問題，避免機械記憶。

五、有助于激發(fā)學生學習的興趣，培養(yǎng)學生的思維

心理學試驗告訴我們，差別大的東西、異常的信號，往往會刺激到我們的大腦，首先引起我們的注意；同樣的東西，從不同的角度去看，會有不同的感覺，給人以新鮮感，讓人產(chǎn)生繼續(xù)了解的欲望。反例教學具有直觀、生動、易懂的特點，教師恰當?shù)剡\用反例能激發(fā)學生學習的興趣，讓學生在探索的過程中展開想象，享受創(chuàng)造的樂趣。

在講授《實數(shù)》一節(jié)時，筆者在練習中設計了一道題：“請判斷以下說法是否正確：①兩個有理數(shù)的和一定是有理數(shù)；②兩個無理數(shù)的和一定是無理數(shù)。”學生對這兩種說法的正確性展開了討論，尤其是在對②進行討論時，舉出了如[3]和-[3]，[π]和-[π]等反例，它們都互為相反數(shù)，和都等于0，0是有理數(shù)。有一名學生給出這樣的例子：a=1.01001000100001……，b=2.10110111011110……，a與b都是無理數(shù)且不互為相反數(shù)，但a+b=3.11111111111111……卻是一個無限循環(huán)小數(shù)，是有理數(shù)。這名學生給出的例子更進一步說明了說法②是錯誤的。通過舉反例，學生對有理數(shù)與無理數(shù)的學習充滿興趣，更深刻地認識有理數(shù)和無理數(shù)，也引發(fā)了學生進行更深刻討論：兩個無理數(shù)的差會是有理數(shù)還是無理數(shù)呢？積呢？一個有理數(shù)與一個無理數(shù)的和、差、積又會分別得到有理數(shù)還是無理數(shù)呢？學生由被動學習轉向主動學習。

反例教學是借助少量有針對性、有代表性的反面例子與正面例子進行比較，讓學生獲得全面的、完整的知識，掌握概念的本質。但是如果反例的引入時機不對，或反例繁雜、沒有針對性，就會讓學生更迷糊，弄巧成拙。所以，教師選取的反例必須從教學實踐中來，真實而生動；必須少而精煉、有針對性、典型性；必須適時而入，循序漸進。

總之，在數(shù)學教學中恰當?shù)剡\用反例教學，能使學生全面、深刻地認識和理解數(shù)學概念，鞏固和掌握性質、定理，克服思維定式，發(fā)現(xiàn)問題、糾正錯誤，發(fā)散思維。因此，教師應加強對反例教學的研究，在教學中更靈活地運用反例教學、更好地把控課堂。

（責編 劉小瑗）