試析建模思想在初中數(shù)學復(fù)習中的應(yīng)用

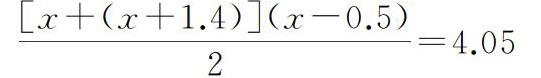
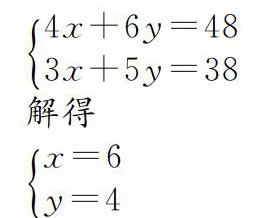
摘 要：數(shù)學建模思想在初中數(shù)學復(fù)習中的應(yīng)用，有利于學生利用數(shù)學原理解決問題，是提高數(shù)學應(yīng)用能力的有效方法。隨著教育改革的持續(xù)推進，對于建模思想在初中數(shù)學復(fù)習中的應(yīng)用的重視程度不斷提高，通過建模思想，如何幫助學生提高綜合運用數(shù)學知識與技能求解的能力是現(xiàn)階段初中數(shù)學教師關(guān)心與研究的重點問題。本文主要分析解答建模思想在初中數(shù)學復(fù)習中的應(yīng)用的相關(guān)問題，通過大量初中數(shù)學教學案例的闡述，希望能夠更加直觀清晰的表達觀點，發(fā)揮參考與借鑒的作用。

關(guān)鍵詞：數(shù)學建模;建模思想;初中數(shù)學;復(fù)習應(yīng)用

在建模思想的引導(dǎo)下，學生在進行初中數(shù)學復(fù)習時能夠?qū)㈩}目與現(xiàn)實生活相聯(lián)系，采用具體的事物特征或數(shù)量關(guān)系幫助鞏固學習成果，加深數(shù)學理解，完成作業(yè)題目。養(yǎng)成運用建模思想的習慣，學生的初中數(shù)學復(fù)習將變得高效、生動，不僅能提高學習效果，更能實現(xiàn)認知、邏輯、思考等素質(zhì)能力的綜合提高。

一、 數(shù)學建模的主要步驟

數(shù)學建模本質(zhì)上是一種數(shù)學語言，是一種進行數(shù)學學習時的典型思考方式，通過將現(xiàn)實問題抽象為數(shù)學模型，再運用數(shù)學方法完成模型求解，從而驗證模型是否具備合理性，在這一過程中，學生對數(shù)學的理解將加深，創(chuàng)造能力與實踐能力將提高。一般情況下，數(shù)學建模需要七個步驟，具體分析如下：

模型準備：了解問題的實際背景，明確問題的實際意義，掌握問題的相關(guān)信息，將問題內(nèi)容轉(zhuǎn)換成數(shù)學語言，利用準確語言描述數(shù)學問題。

模型假設(shè)：找準建模對象特征，明確數(shù)學建模目的，簡化數(shù)學問題內(nèi)容，提出合理數(shù)學假設(shè)。

模型建立：在合理數(shù)學假設(shè)的基礎(chǔ)上，利用數(shù)學工具建立各變量之間的數(shù)學關(guān)系，完成數(shù)學結(jié)構(gòu)的建立。

模型求解：利用模型相關(guān)的數(shù)學信息與數(shù)據(jù)資料，對所有參數(shù)進行計算解答。

模型分析：綜合利用數(shù)學邏輯及方法，對數(shù)學計算解答而得的結(jié)果進行數(shù)學合理性的分析。

模型檢驗：將模型分析結(jié)果與實際情況進行比對，以判斷結(jié)果是否具備合理性、科學性與適用性。

模型應(yīng)用：根據(jù)模型準備與假設(shè)時的目的，應(yīng)用數(shù)學模型。

二、 數(shù)學建模的主要作用

首先，通過數(shù)學建模，能夠?qū)?shù)學與其他學科進行聯(lián)系，使學生感受到數(shù)學的強大功能與應(yīng)用價值，從而激發(fā)學生對數(shù)學學習的熱情。

其次，通過數(shù)學建模，能夠鍛煉學生的綜合能力，這些能力主要包括想象力、邏輯思維能力、數(shù)學語言表達能力、問題提煉能力、合作交流能力等。

再次，通過數(shù)學建模，學生在復(fù)習時能夠獲得主動性，能夠?qū)?shù)學知識與題目內(nèi)容與實際相結(jié)合，甚至能夠引導(dǎo)學生通過社會活動建立數(shù)學模型，符合現(xiàn)階段素質(zhì)教育的具體要求，有利于初中數(shù)學學習效果的提升。

最后，通過數(shù)學建模，能夠使學生掌握數(shù)學應(yīng)用的基本方法，從而去完成數(shù)學建模的實施與操作，能夠體現(xiàn)數(shù)學學習的深遠意義與學科價值。

三、 建模思想在初中數(shù)學復(fù)習中的應(yīng)用

在初中數(shù)學教學中，數(shù)學建模是極為常見、常用的思維方法與解題方式，由此可見，建模思想應(yīng)是學生在進行初中數(shù)學復(fù)習時最應(yīng)該強化練習，力求掌握的數(shù)學方法。初中數(shù)學所包括的典型數(shù)學模型包括方程、不等式、函數(shù)、幾何、圖表等，下文將舉例分析建模思想在初中數(shù)學復(fù)習中的應(yīng)用。具體內(nèi)容如下：

（一） 方程建模

方程建模是最為基本的數(shù)學模型，其主要是利用數(shù)量的相等關(guān)系解決一些問題，在解決工程問題、銷售問題、利率問題等問題時，方程建模的準確性、清晰性、邏輯性特點凸顯，實際應(yīng)用具有良好效果。

例題1 某水庫計劃修建一條橫截面為梯形的輸水渠道，已知橫截面面積為4.05m2，上口寬比渠底寬1.4m，渠深比渠底寬小0.5m。求渠道的上口寬與渠深分別是多少。

分析：聯(lián)系實際生活，問題本身屬于工程問題，在建模思想的引導(dǎo)下可嘗試使用方程建模予以解決，運用到的數(shù)學知識還主要涉及梯形面積的計算公式。

解：假設(shè)渠底寬為x，則上口寬即為x+1.4，渠深即為x-0.5，已知梯形橫截面面積為4.05m2，利用梯形面積計算公式建立方程，即為

[x+（x+1.4）]（x-0.5）2=4.05

解得x1=2，x2=-2.2，x2不合題意所以舍去，得出渠底寬為2m。

答：上口寬為2+1.4=3.4m，渠深為2-0.5=1.5m。

例題1是比較簡單的方程建模，還有一些問題需要利用方程組建模進行解答，比如“雞兔同籠”的問題。

例題2 買四只雞、六只兔時，一共需要花費48元，而當買三只雞、五只兔時，一共需要花費38元。問雞和兔的單價分別是多少？

分析：“雞兔同籠”問題是古代一個復(fù)雜的數(shù)學問題，但是利用建模思想就可以輕松解答，進行方程組建模的關(guān)鍵就是題干中的兩組等量關(guān)系。

解：假設(shè)雞的單價為x元，兔的單價為y元，則建立方程組模型如下

4x+6y=483x+5y=38

解得

x=6y=4

答：雞的單價為6元，兔的單價為4元。

（二） 不等式建模

等量關(guān)系存在的同時，不等量關(guān)系也具有普遍性，尤其是在分配問題、營銷問題、統(tǒng)籌問題等問題上，不等量關(guān)系比等量關(guān)系存在的可能性更大，在遇到這一類問題時，就需要利用不等式建模，對實際問題進行解決。

例題3 某校組織學生春游，有若干名學生，準備了若干輛校車，如果每輛校車坐4名學生，則余下18名學生沒有車可坐;如果每輛車坐6名學生，則有一輛車坐不滿。問一共有多少名學生和多少輛校車？

分析：通過閱讀題干，提煉信息，可以發(fā)現(xiàn)這是一個不等量數(shù)量關(guān)系，由此可建立不等式模型，考慮實際情況中學生與校車只可能為正數(shù)和整數(shù)，則可以確定合理答案。

解：假設(shè)該校安排校車x輛，則有（4x+18）名學生，可建立不等式方程如下

（4x+18）-6（x-1）>0（4x+18）-6（x-1）<6

解得

9

∵校車數(shù)為正整數(shù)

∴x=10或者x=11

當x=10時，4x+18=58;當x=11時，4x+18=62

答：該校一共有學生58名，安排校車10輛;或者有學生62名，安排校車11輛。

（三） 函數(shù)建模

函數(shù)的本質(zhì)是事物之間的廣泛聯(lián)系，是量與量之間的依存關(guān)系，包含數(shù)量關(guān)系及變化規(guī)律，常見的如解決成本問題、利潤問題、優(yōu)化問題等問題都可以利用函數(shù)建模予以解決。在初中數(shù)學復(fù)習中，函數(shù)建模的相關(guān)運用占有較為關(guān)鍵的位置，通過函數(shù)建模，著力培養(yǎng)學生用函數(shù)看待、解釋、解決問題的思維習慣及應(yīng)用能力，實現(xiàn)學生數(shù)學思維意識的提高。

例題4 某省濕地公園面積12萬公頃，規(guī)劃今后10年每年擴建面積相同，約為0.61到0.62萬公頃。請預(yù)估6年后該省濕地公園總面積為多少萬公頃。

解：假設(shè)P為該省今后10年每年擴建的公頃數(shù)，根據(jù)題意0.61≤P≤0.62，用S表示6年后該省濕地公園總面積（單位：萬公頃），則S=6P+12。

根據(jù)一次函數(shù)性質(zhì)，一次項系數(shù)k=6>0，所以S會隨P的增大而增大。

∵0.61≤P≤0.62

∴6×0.61+12≤S≤6×0.62+12，即15.66≤S≤15.72

答：6年后該省濕地公園總面積將在15.66萬公頃和15.72萬公頃之間。

例題4是比較簡單的一次函數(shù)建模，較為復(fù)雜的一次函數(shù)建模還可利用等式方程建模、不等式方程建模等進行問題的解決。

（四） 圖表建模

圖表建模的最大優(yōu)勢是通過條理清晰，直觀明確的方式將數(shù)學信息進行梳理列舉，按照不同的類型將數(shù)學信息進行排列，以方便對問題進行解決，而且利用圖表不容易遺漏關(guān)鍵信息。利用圖表建模可以對頻率、分類、統(tǒng)計等問題進行有效解決，在實際的應(yīng)用當中具有普遍性。特別是在研究工作以及論文寫作當中，圖表具有不可忽視的作用，其有利于發(fā)現(xiàn)各種變量之間的關(guān)系，生動、形象地使復(fù)雜和抽象的問題變的直觀、清晰，可以代替大量的復(fù)雜的文字說明，節(jié)省篇幅。

例題5 人類有A、B、O和AB四種血型。在學校組織的一次體檢中，一班的血型檢測結(jié)果是在40名學生當中，A型16人，B型5人，O型有45%，剩余都是AB型。二班的血型檢測結(jié)果是在45名學生當中，A型有40%，AB型2人，O型20人，剩余都是B型。請制作能說明一班和二班血型統(tǒng)計情況的圖表。

解：要想繪制能說明一班和二班的血型統(tǒng)計情況的圖表，要先確認一班和二班的每種血型的人數(shù)，那么現(xiàn)在未知的就是一班的O型和AB型，二班的A型和B型。

根據(jù)題目信息，先確認一班的O型和AB型。

∵一班的O型占一班人數(shù)的45%

∴O型人數(shù)為40×45%=18人，為此AB型人數(shù)為40-16-5-18=1人

再確認二班的A型和B型。

∵二班的A型占二班人數(shù)的40%

∴A型人數(shù)為45×40%=18人，為此B型人數(shù)為45-18-2-20=5人

一班和二班人數(shù)確認后，即可進行血型統(tǒng)計表的繪制。

通過例題5，可以明確地看出如何進行圖表建模，首要問題是利用數(shù)學方法處理題目中的量與量之間的關(guān)系，由此將繪制圖表中所涉及的數(shù)學信息進行全部確認，最終完成圖表的繪制。

四、 結(jié)語

綜上所述，建模思想是初中數(shù)學復(fù)習中常見且必要的數(shù)學知識要點，通過建立數(shù)學模型解決問題，有利于使學生掌握運用數(shù)學知識解決實際問題的方法，從而實現(xiàn)數(shù)學學習效果的提高，熱情的增加，理解的加深。基于此，初中數(shù)學教師在安排相關(guān)復(fù)習任務(wù)時，應(yīng)選擇與實際生活情況有所貼近的學習資料，并大力鼓勵學生們運用建模思想去思考問題、解決問題，并且在平時的初中數(shù)學教學當中，教師也應(yīng)該有意識的加強對數(shù)學建模內(nèi)容的授課，幫助學生樹立關(guān)于建模思想的系統(tǒng)認識與理解。

參考文獻：

[1]高仕聰.初中數(shù)學教學中運用建模思想的研究[J].兒童大世界（下半月），2019（3）：33.

[2]李春香.淺談如何在初中數(shù)學教學中滲透建模思想[J].魅力中國，2019（3）：4.

[3]張華富.數(shù)學建模專題復(fù)習教學初探[J].中國數(shù)學教育（初中版），2019（7）：34-37.

[4]于春梅.構(gòu)建數(shù)學模型，培養(yǎng)核心素養(yǎng)—探究初中數(shù)學路徑最短問題的解決策略[J].中學數(shù)學，2019（16）：65-66.

[5]許波琴.建模思想在初中數(shù)學中的體現(xiàn)[J].數(shù)學大世界（中旬版），2019（6）：9-10.

[6]劉榮.建模思想在初中數(shù)學復(fù)習中的應(yīng)用[J].中學數(shù)學，2019（18）：28-29.

[7]王衛(wèi)軍.基于初中數(shù)學核心概念及其思想方法的概念教學設(shè)計——“代數(shù)方程的復(fù)習（1）”的實踐[J].上海中學數(shù)學，2016（12）：43-45，48.

[8]崔慧.運用建模思想解答數(shù)學問題[J].數(shù)理化學習（初中版），2014（8）：23.

[9]藺麗娟.淺談初中數(shù)學復(fù)習課中建模思想的應(yīng)用[J].山東教育（中學刊），2013（11）：80-82.

作者簡介：童紀江，浙江省余姚市，浙江省余姚市姚江中學。