此處“無聲”勝“有聲”

薛峰

[摘? 要] 知識與智慧是在無聲無息的積累中生成的，在初中數學教學過程中，我們需要借助知識與技能的循序漸進，達成潤物細無聲的效果，達到此時無聲勝有聲的效果.

[關鍵詞] 初中數學;緘默知識;內隱知識

緘默知識又稱為“內隱知識”，它相對于顯性知識，是一種體現在行動中卻無法用言語、文字、符號等表述的知識，它廣泛地存在于人的認知過程中，是人認知事物和解決問題時所依賴的一種理解和確信. 緘默知識雖“不可名狀”，但它卻是真實存在的，日常生活中的很多現象可以解釋這一點：比如學習自行車，大家都知道“保持平衡”這一技巧，但究竟如何保持身體平衡不摔倒，卻無法用語言表達清楚，需要我們經過多次練習和摔倒來自己體會，這就是緘默知識的存在. 在學習中，緘默知識無處不在，筆者從教初中數學多年，認為緘默知識在數學學習中常常存在于“為什么這樣想”“為什么這樣做”的過程中，緘默知識是能力的一種體現. 在教學中緘默知識雖然無法描述，卻是可以傳遞的，下文筆者結合實例簡要談談如何將緘默知識在初中數學教學中進行傳遞.

傳遞前提：感知緘默知識的

意識是能力形成的基礎和前提，讓學生意識到緘默知識的存在是培養學生形成與強化緘默知識的先決條件. 雖然每個學生都會存在各個方面的緘默知識，但要讓學生感知到它的存在還需通過教師的引導，教師可以通過直接或間接的方法讓學生感知到緘默知識的存在.

1. 直接法

即讓學生感知緘默知識的存在，教師可以通過各種資源查找和整理有關緘默知識的內容，整合成PPT，在班會課的時候呈現給學生. 在實施前不難預見，學生對“緘默知識”這一概念的理解會感到困難，因為這本身就是很抽象的一個名詞，因此引用更多的實例來輔助說明可以幫助學生理解. 比如在日常生活中，有人會對之前走過的路了如指掌，而有些人卻是‘路癡，走過好幾遍的路還是不認得，然而前者并沒有刻意去記憶每一條路，問他如何記住路，他也無法描述. 再如在數學解題中，尤其是幾何綜合問題，“思路”是我們講得較多的一個名詞，然而有些問題的條件指向性不強，不知道從什么角度去考慮問題，當你看到答案時卻豁然開朗，這兩者之間便是緘默知識的存在. 在生活與學習中，這樣的實例很多，教師可以去挖掘，以實例來幫助學生理解緘默知識的含義，促進學生形成對緘默知識的認識.

2. 間接法

間接法即在潛移默化中讓學生感知緘默知識的存在. 在教學內容中，數學美就是典型的緘默知識，英國數學家哈代說過“數學美可能很難定義，但它卻是一種真實的美，和任何其他的美都一樣”. 在教學中讓學生領略數學的符號美、對稱美等，不需要語言描述，學生自會體悟到這種美的存在，這便是感知到了緘默知識的存在. 在教學過程中，緘默知識存在于教師創設情境、激發學生創造性的過程中，學生創造能力的形成便是緘默知識的增長. 在解決問題的過程中，緘默知識體現為介于邏輯思維與直覺思維之間的一種思維形式，該種思維形式是找到問題突破口的重要條件，也是緘默知識的真實存在的證明.

只有讓學生感知到緘默知識的存在才會促使他們去挖掘緘默知識，引起對緘默知識的重視，從而有意識地從緘默知識出發來提高自己的數學能力.

傳遞過程：挖掘緘默知識的作用

緘默知識的重要性已在上文提及，而其作用需要教師去發現、去挖掘. 在教學中，教師首先要對緘默知識形成正確的認識，肯定其重要性，并充分挖掘數學教學中的緘默知識，在此基礎上有意識地將其傳遞給學生. 例如可以從以下幾個方面去傳遞.

1. 概念教學：留有余地

概念是數學知識的基本依據，理解概念是掌握數學知識的先決條件，也是解決問題的基礎. 理解概念并不只是知道概念的內容，更重要的是知道概念的內涵，學會它的用法，而理解概念的過程便是緘默知識的形成過程.

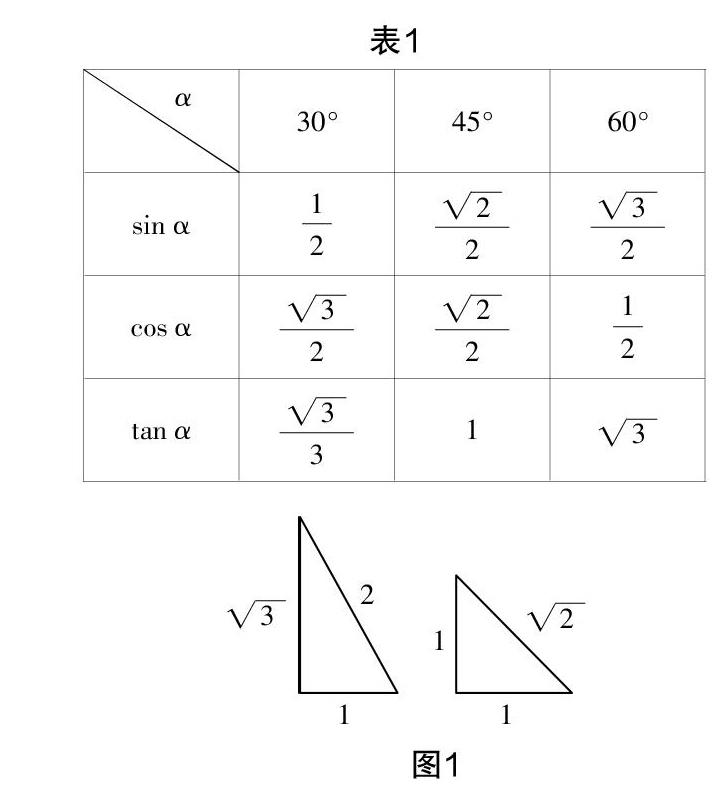
如特殊角的三角函數值是解特殊直角三角形常用的依據，也是計算題中出現頻率較高的內容，但在教學中卻發現，許多學生對表1中的數據經常會出現“記不住”或混淆的情況，其實這就是沒有完全掌握概念的實質.

如果將上述表格中的內容當成是背誦內容，其效果可想而知. 教師可以在與學生共同推導出特殊角的三角函數值以后給學生幾分鐘的時間，讓學生用自己的方法將表格中的數據在理解的基礎上熟練掌握，而后可以讓部分學生交流他們所使用的方法. 在這個過程中，學生提到了“只記分母”“看數字的增減性”“不需要記表格中的數據，只需熟練正弦、余弦和正切的求法，利用圖1兩個特殊直角三角形結合特殊的邊長即可很快求出”等方法，以上方法雖然都是可以描述的，但是通過這樣一種方式可以給學生提供獲取緘默知識的空間[1]. 在概念教學中，出示了一個概念之后教師要留有一定的時間給學生掌握和消化概念，這樣才能促進緘默知識的形成.

2. 數學閱讀：學會分析

數學閱讀能力是數學理解能力的重要決定因素，具有良好的數學閱讀能力也是順利解決數學問題的基本要素. 在教學中會發現，數學閱讀能力無法系統地進行“指導”，教師更多的是讓學生注意平時的積累，積累的過程實則緘默知識的增長過程，而這個過程中，教師可以通過一定的指導來助長它.

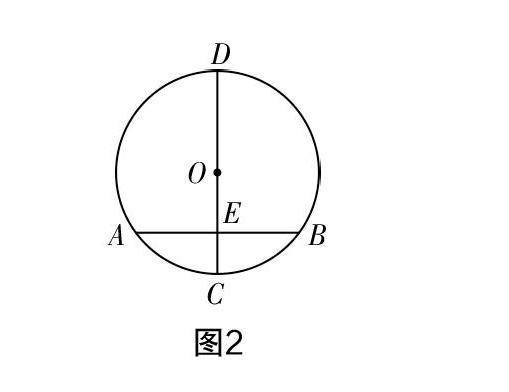
如垂徑定理的教學中，垂徑定理的內容是教學重點，即“垂直于弦的直徑平分弦，并且平分弦所對的兩條弧”. 短短兩句話，有學生很快能領悟其中的內涵，也有很多學生感覺難以理解，更不知道如何去使用. 如果讓學生機械背誦記憶自然效果不佳，結合圖形教學可以在一定程度上改善效果，但依舊有一定的局限性. 可以嘗試這樣引導學生：將定理的內容如同古詩詞一樣進行朗讀劃分，“垂直于弦的/直徑/平分/弦，并且/平分/弦所對的兩條弧”，這樣可以幫助學生從語文的角度理解句子，找到定理的主語“直徑”，修飾主語的定語是“垂直于弦”，主語后面是謂語和賓語，再結合圖2即可幫助學生理解其含義.

上述教學中教師通過簡單分析句子成分的過程即可讓學生學會抓重點，掌握數學閱讀的方法，除此之外，找關鍵詞、圈畫法、問題羅列法都是提高數學閱讀能力的方法. 在實踐中，教師可以針對不同的問題通過簡單的閱讀指導讓學生提高閱讀能力，改善學生對數學文字“望而卻步”的現象. 通過上述指導，教師不僅幫助學生提高了閱讀能力，同時在無形中將積累緘默知識的方法傳遞給了學生.

3. 問題解決：重視方法

問題解決過程中的緘默知識通常體現在解決問題的第一步，即“如何解決”“選擇怎樣的方法解決”. 眾所周知，數學是一門需要積累的學科，在做了大量的題目之后即可擁有一定解決問題的經驗，確保遇到新的問題時能夠得心應手，其實這就是緘默知識比較豐富的體現. 教師在對幾何問題證明的教學過程中可以突出思路、思想及方法的傳授，通過這樣一個過程可以促進緘默知識的形成.

以如下問題為例：在直角坐標系xOy中，點O（0，0），動點A（t，t）在第一象限，動點B（0，m）在y軸上. 當AB=4時，△OAB面積的最大值為（? ? ? ）

A. 8? ? ? ? ? ? ? B. 4+4

C. 4-4 D. 8

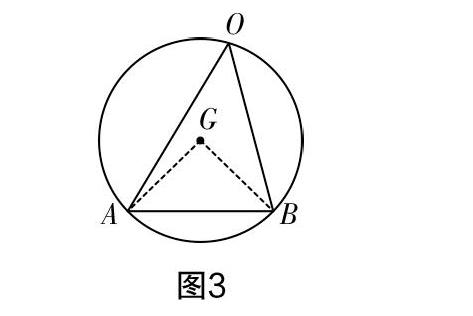
在解決這個問題時，學生因為看到了坐標所以通常會先建立直角坐標系，這是常規的思維，但是隨后就會發現無法解決問題，大部分學生隨即選擇放棄，因此該問題的錯誤率極高. 其實該問題并不是用坐標來解決，而是將O，A，B三點置于圓中，如圖3，當點O到AB的垂線段經過圓心時，三角形的面積最大.

教師在講評該問題時可以引導學生這樣思考：△OAB中∠O是確定的，AB的長也是確定的，但是點O與AB的位置關系卻是不斷發生著變化，這樣的位置關系會存在于什么圖形中呢？三角形中，底邊長度恒定，是什么元素決定了三角形的面積呢？題后可以再次對三角形面積的求法做相關的總結：直接法、補形法、分割法等，讓學生對該類問題積累更多的方法.

緘默知識在解決問題中是一種能力的體現，因此教師在講解問題時一定要主動進行方法的總結與思想的傳遞，這樣才能幫助學生挖掘自己的內隱知識，促進緘默知識的增長，提高學生解決問題的能力.

緘默知識是我們常常說的“只可意會不可言傳”的知識，其中的“意會”便是傳遞的一種方式. 我們雖然無法描述，但卻可以感知到它的存在，它存在于教學的任何一個細節中，可以在教學中進行傳遞，可以從側面進行推進. 在初中數學教學中對緘默知識的傳遞是筆者的一次嘗試，其效果需要更多的實踐與反思，只有在不斷的調整與改進中才能讓這種無聲的知識發揮作用，真正做到“無聲勝有聲”.

參考文獻：

[1]侯燕. 緘默知識視角下學生研究性學習能力的形成機制及其應用[D].四川師范大學，2011.