聯想法在小學數學教學中的應用
陸義春 梁宇
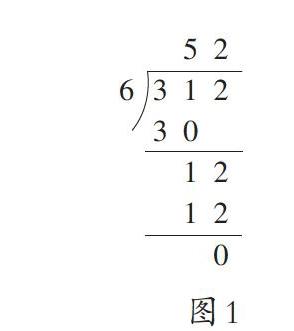
【摘要】本文以類比聯想、接近聯想、對比聯想和數形聯想為例,闡述聯想法在小學數學教學中的具體用法,呼吁教師融會貫通,發揚聯想法在數學教學中的廣泛應用。
【關鍵詞】小學數學 類比聯想 接近聯想 對比聯想 數形聯想
【中圖分類號】G 【文獻標識碼】A
【文章編號】0450-9889(2019)08A-0136-02
聯想在數學中指由某個知識引起另一知識的思維形式,是打開思路、轉換思維和發現真理的重要手段。數學聯想的實質是知識的遷移,聯想到的知識與新知識之間有一定的聯系或相似性,它為新知識的學習提供一定的知識基礎、方法、模型等,有利于學生對新知識的理解和掌握。
一、類比聯想
類比聯想是指想要了解一類事物的某些特征,聯想到與其在某些方面如形狀、數量、功能、性質、屬性、結構等有相似性的另一類事物,猜測兩者在其他方面也可能有類同之處,以熟知事物的特征來做出某種判斷,類比是探究新事物特性的一種重要且有效的教學方法。在數學教學中,類比聯想通常是學習概念、方法、定理和公式的重要手段。
例1 除數是兩位數的除法的計算
在學習本節知識時,可聯想除數是一位數的除法的解題思路。以復習導入的形式,結合新知例題,在假設與解題過程中概括出兩位數除法的計算法則,不僅簡化了教學過程,而且在舊知的基礎上,學生也更容易接受和領悟。
(一)復習導入:由學生講解除式312÷6=52的解題思路并呈現豎式步驟。
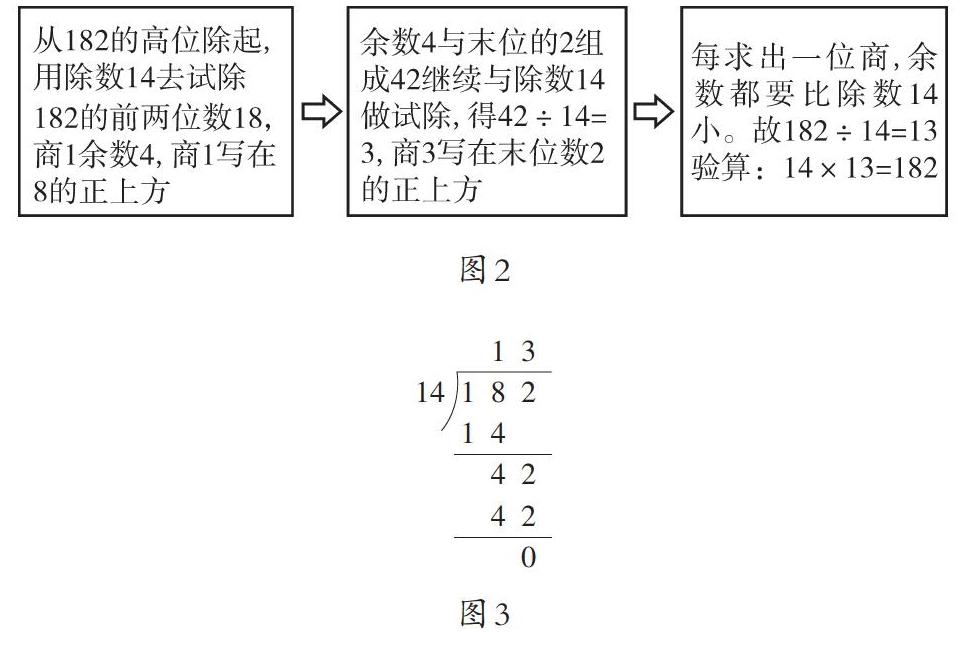
(二)聯想類比:在以上思路和方法的基礎上,結合“除數是兩位數”這一具體條件,猜想其計算法則與除數是一位數的除法類同,并在實例182÷14=13中證實這一猜想的正確性。
(三)概括總結:由學生結合運算過程、模仿已學法則概括出除數是兩位數的除法的計算法則。
二、接近聯想
接近聯想是指由某知識聯想到另一個與之接近的知識,也就是新知識的學習過程或運用的方法與某一舊知識的學習很接近,進而從舊知識中獲得啟發,技巧性地展開對新知識的學習和分析。引導學生進行接近聯想,著眼于由舊知學習新知,對舊知進行重組和轉化,進而形成新知,充分啟發學生的思維,簡化學習過程。
例2 三角形面積計算公式的推導
(一)聯想舊知:學生在看到《三角形的面積》這一課題時,很快就能聯想到上一課時剛學過的課后練習題第10題(人教版數學五年級上冊第90頁)。題目中的平行四邊形,被它的一條對角線分成兩個三角形。學生通過數格子得出,平行四邊形面積是涂色三角形面積的2倍。通過觀察和測量兩個三角形面積,學生知道分割后出現的兩個三角形完全相同。
(二)思路點撥:題目的實質就是讓學生對同底同高的三角形與平行四邊形面積之間的關系有一個初步的猜想,埋一處伏筆,為下一課時三角形面積的學習鋪墊。
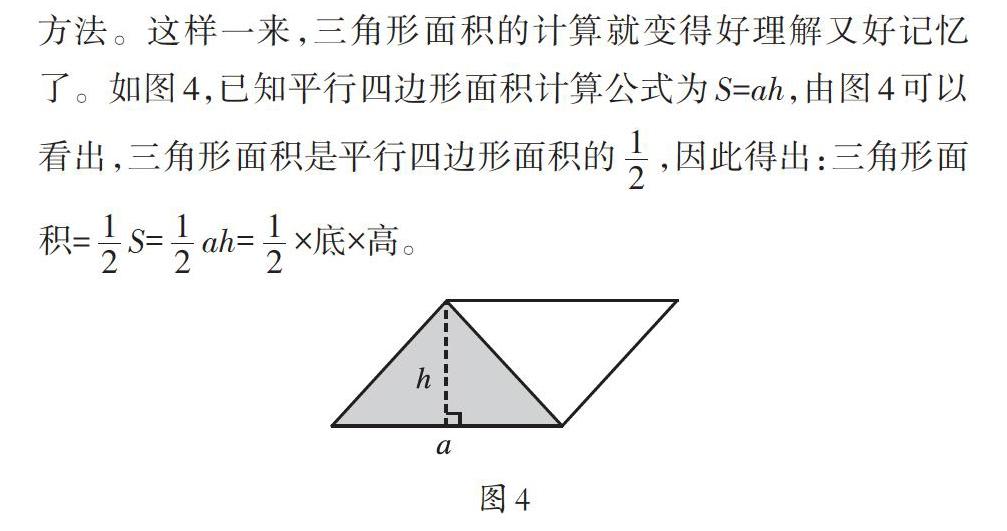
(三)新舊轉化:當把三角形面積的計算作為一個新知識進行學習時,教師就可以按照上題的結論合理安排,利用接近聯想,引導學生通過旋轉、移接操作把兩個同樣的三角形拼成一個平行四邊形,通過新舊知識的轉化間接得出三角形面積的計算方法。這樣一來,三角形面積的計算就變得好理解又好記憶了。如圖4,已知平行四邊形面積計算公式為S=ah,由圖4可以看出,三角形面積是平行四邊形面積的[12],因此得出:三角形面積=[12]S=[12]ah=[12]×底×高。
三、對比聯想
對比聯想是指在遇到某一問題時,先聯想到其反面例子,考慮到與其性質或特點相反的問題,借助逆向思維來尋求解決問題的方法。在加法與減法、乘法與除法、約分與通分、同分母和異分母、正負數、正比例與反比例等的教學中利用對比聯想,常常可以取得不錯的效果。
例3 正、反比例的判斷
正確判斷關聯量的反比例關系是否成立是學習反比例的重點和難點。因此,在探究伊始,可以以正比例作為對立面打開思路,通過逆向思維和強烈的對比,加深學生的印象。教師可以用一組包含正、反比例的題目切入,既“溫舊習新”,又起到了“以新襯舊”“互比互鑒”的效果,兩組知識點都得到了強化。
例如:車間要完成5280臺機器的組裝任務,要求每天組裝480臺,11天完成。如果5280臺用工作總量N表示,每天組裝480臺用效率p表示,11天用時間t表示。
(1)N與t、N與p分別成什么比例關系?(復習正比例,感悟關聯量的變化相隨)
(2)t與p是什么關系?(分析關聯量的變化關系,引出反比例)
通過分析關聯量的變化相隨關系,由[Nt=p]和[Np=t]的正比例關系反推它們之間的反比例關系,從而在意義和形式上展開對反比例的學習。同時,正、反比例的相互對比使得學生對兩種知識的掌握更清晰、更牢固,判斷關聯量的關系時也更加得心應手。
四、數形聯想
數形聯想又稱直觀聯想,是依據抽象與具象的相對關系和合理互轉性分析數學問題的一種方法。采用數形聯想能使抽象的問題變得具體直觀,更接近學生的理解能力,很大程度上降低學生學習數學知識的難度,優化解題步驟,進而讓學生的數學學習興趣得以激發,促進教學質量的提升。
例4 24時計時法——經過時間的計算
小白和爸爸媽媽一起坐火車去奶奶家,已知火車上午9:00出發,下午6:00到站。算一算小白到奶奶家要坐多長時間的火車,和同學交流一下你是怎么想的。
思路1:教師在教學過程中,鼓勵學生手腦結合,頭腦中想象有一個轉動的鐘表,同時伸出手指,跟著節奏數數:時針從上午9時到上午10時、上午11時、中午12時、下午1時……下午6時,共經歷9個小時。
思路2:由具體的時間上午9:00和下午6:00聯想到鐘表直觀,引導學生運用鐘表時針的轉動來解決此問題。教師可以取出鐘表直接現場演示撥時針,或者借助多媒體課件動態地演示時針轉動的過程。如圖5,時針從上午9時轉動到下午6時,經過了9個大格,每個大格表示1個小時,所以小白到奶奶家共坐了9個小時的火車。
思路3:引導學生由上午和下午的間隔聯想到分段計時法,用畫線段的方法表示時間的推移。以中午12時作為分界線,從上午9時到中午12時的3個小時為第1個時間段,從中午12時到下午6時的6個小時為第2個時間段,兩個時間段相加即為所用時間的總和,所以3+6=9(小時),小白到奶奶家共坐了9個小時的火車。
數學學習中的聯想就是師生思維的展開和發散,聯想法在小學數學中的合理運用能使陌生的概念熟悉化、抽象的題目形象化、單一的方法多樣化、晦澀難懂的問題簡單化,方便學生理解,助益教學效果和教學質量的提升。教師不僅要認識和了解聯想法,還要會用、用好、好用聯想法,方便教學的同時提升自己的專業素養。另外,教師在自身用好聯想法之余,還應多多向學生滲透聯想法在數學學習中的廣泛應用及其價值,促進學生思維的發展和解題能力的不斷提升,力求學生在簡單、有趣的數學學習中找到自信,不畏數學,輕松學習、快樂學習。
作者簡介:陸義春(1993— ),女,河南周口人,南寧師范大學初等教育學院在讀碩士研究生,研究方向:小學數學教育。
梁宇(1978— ),女,廣西賀州人,教授,碩士研究生學歷,研究方向:小學數學教育及教師發展。
(責編 劉小瑗)

