讓思想在課堂里涌動

尹宇

摘 要：隨著素質教育的提出，現下教學越來越注重培養與提升學生的綜合素養。小學階段，學生的思維處于發展的活躍階段，此刻展開的教學與引導是學生以后學習與發展的基礎。小學數學中存在著很多的數學思想，這些數學思想是數學知識的精髓與靈魂，在實際教學中教師要合理利用科學的教學方式滲透數學思想。探討小學高段空間圖形學習的現狀，分析學生在學習空間圖形過程中存在的問題，并在此基礎上探討在小學數學高段空間圖形中滲透數學思想的重要性，以及探究小學數學高段空間圖形中滲透數學思想的教學策略，以此作為小學數學空間圖形教學中滲透數學思想的參考依據，旨在提升小學數學空間與圖形的教學質量與效率。

關鍵詞：小學數學;空間與圖形;數學思想

數學知識主要由概念、性質、法則、公式、數量關系、解題方法構成，但是數學并不是這些簡單的組合，數學還涉及較多的數學思想與方法。數學思想，即人們在數學知識的學習過程中對數學理論與內容的本質認識，是從理論知識中提煉出來的具備更高層次水平的觀點，是數學普遍規律的一種揭示，關系與影響著數學的實踐活動。另外，數學思想以數學知識為載體，并超脫數學知識，是一種運用數學知識合理解決實際問題的能力與方法。在實際教學中，教師要注重在教學中滲透數學思想，引導學生真正領悟數學知識，培養與提高學生應用數學知識解決實際問題的能力，為學生更好的發展與提升打下良好的基礎。

一、小學生空間圖形學習的現狀

在小學生空間圖形教學中，理論教學知識占據的比重過大，受其身心特點的影響，學生對理論知識并不是特別感興趣，相應的學習效果可想而知。此外，教師的課堂教學方式單一，一些教師依舊使用傳統灌輸式教學方式傳授教學知識，不利于學生思維的發散與培養，阻礙學生空間想象能力的提升與發展。在實際教學中，教師忽略教學主動，沒有在教學中調動學生的積極性與主動性，很多學生處于被動學習的狀態，致使學生逐漸喪失學習興趣。

二、小學數學思想方法在高段空間與圖形教學中滲透的重要性

在小學高段“空間與圖形”教學中滲透數學思想，不但能促使學生理解與掌握相關數學知識與基本技能，還在一定基礎上有利于拓展學生思維，啟發學生智力，實現學生自身潛能的挖掘以及培養學生思想道德品質與非智力因素。數學思想的滲透可以幫助學生建立更強的數學觀念，促使學生在學習的過程中養成良好的思維素質，更好地實現素質教育。小學數學知識重要，數學思想更為重要，這兩點是小學數學教材中重要的主線。在數學思想的滲透下，數學知識不再是簡單的概念與性質記憶，數學方法也不再止步于單一的教學方式，可以實現學生對教學內容的整體把握。小學數學教學應該緊隨時代發展，適應國際數學教學發展以及社會發展。在小學數學中滲透數學思想，有助于提升學生的綜合素養，為學生以后在社會中的發展打下良好的基礎。并且，小學數學高段空間與圖形教學知識相互獨立與密切聯系。數學思想的滲透可以加強相關數學知識的聯系，引導學生舉一反三，培養學生的創新思維，幫助學生融會貫通所學的數學知識，還有助于學生第三學段學習的過渡。

三、在高段空間與圖形教學中滲透的數學思想

（一）極限思想

這種數學思想主要是引導學生從有限認識無限，教導學生如何借助近似深刻認識精確的概念，是數學思想中一種重要的思想方法，是事物轉化的重要環節，掌握這種思想對學生的發展有著重要的意義。

（二）化歸思想

作為解決數學問題的重要思想，這種思想是指將待解決的問題轉化為較為簡單的問題，輕松解決。在現實世界中，事物不是恒定不變的，而是不斷變化的，應用這種思想可以有效簡化數學問題的解決步驟與過程。

（三）數形結合思想

作為數學教學研究對象的兩個側面，數與形有效地結合空間形式與數量關系，將與之相關的問題綜合起來分析與解決。在空間與圖形教學知識學習時，運用這種思想可以有效找到問題的關鍵，迅速找到解決問題的鑰匙。

（四）符號化思想

在空間與圖形中，需要用符號代表圖形中的頂點，如果沒有符號的統一標注，在實際問題解決中就會顯得十分復雜與雜亂，導致數學知識成為“天書”，因此符號化思想的滲透是十分重要的。

（五）集合思想

將具備相同特質的事物組合成一起，劃分為同類，這種思想是現代思想的基礎，在小學數學教學中多處體現。

四、在高段空間與圖形教學中滲透數學思想的方法與案例

（一）建立數學模型，合理應用學生的想象力滲透數學思想

在空間與圖形學習中，空間想象能力發揮著重要的作用，在實際教學中，空間想象主要依賴空間感知，教師要合理激發學生的空間想象思維，鍛煉學生的空間想象能力，實現學生空間觀念的提高。比如：在直線的無限性質教學時，教師除了可以在教學中進行線段、直線、射線的比較，講解有關直線、射線、線段的概念與知識外，還要講解在真實的世界中并沒有直線與射線，而是人們在腦海中想象并規定的一種數學工具。這種概念的提出是為了數學計算與問題解決的方便。然后，教師可以引導學生想象直線的特征，引導學生在頭腦中塑造直線的模型。在此過程中，教師一定要強調無限延伸，促使學生在腦海中繪制出本質上的直線，并在此過程中滲透相應的極限思想。

（二）合理設置練習，引導學生通過習題感悟數學思想

在實際教學中，教師會發現這樣一種狀況：給學生講解的習題種類很多，但是學生的解題水平仍停留在套用的階段，題干條件稍微出現變化，就會導致學生手忙腳亂，這種狀況下學生不會行成良好的解決問題的能力，更不會產生創新能力。導致這一情況出現的原因主要是由于教師在教學中沒有引導學生感悟數學思想與數學方法，只是讓學生對相關知識進行記憶。為此，在實際教學中，教師要合理設置練習題目，引導學生通過練習進行數學思想的感悟。比如：在圖形面積相關知識講解時，教師可以為學生設置下面一個問題。

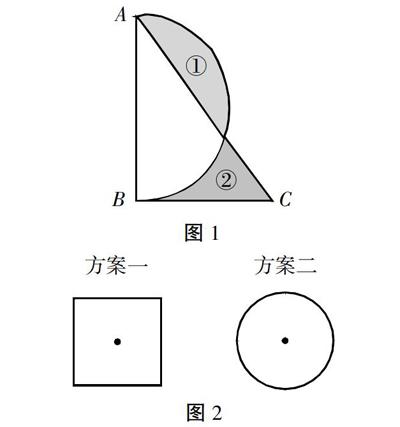
如圖1所示，三角形ABC是直角三角形，AB=4，BC=3，求陰影部分①與陰影部分②的面積相差多少？

通過題干與圖的觀察，可知陰影部分②的面積與空白部分圖形的面積之和與三角形的面積相等，陰影部分①的面積與空白部分的面積之和等于半圓的面積。經過分析，從而可以將面積之差轉化為三角形與半圓面積之差，從而減少計算，簡化過程。

（三）課后總結，在引發學生質疑與反思中滲透數學思想

在教學中，教師要引導學生進行反思與質疑，并提出自己獨特的見解，實現教學質量的提升。如在圓錐體積公式推導教學時，教師可以先提出有關問題引發學生思考與猜測，并引導學生對自己的猜測進行操作驗證，從而對實際問題進行驗證，并在這一過程中推導出相應的結論。應用轉化思想，合理將圓錐面積的求解轉化為三角形與圓弧面積的求解。這一教學過程中，學生會由于好奇心理與質疑心理對探究的內容產生濃厚的興趣，并在驗證過程中體會到學習數學知識的樂趣，在推出結論后，學生體驗到轉化思想與數形結合思想的妙用。

再比如：在“圓的認識”相關內容教學時，教師可以引入一個問題“某班舉辦套圈活動，套圈方案有兩種（如圖2），同學們認為哪種方案更為公平？”引發學生展開討論與思考，總結四邊形與圓形的相關知識，并以此滲透相應的數學思想。在討論過程中，學生會認為方案二更為公平，因為離圓心的距離是相同的，教師可以通過多媒體課件為學生演示無數個點組成圓的過程，以此滲透集合數學思想。

參考文獻：

[1]李銀銀.小學高段“空間與圖形”教學中數學思想滲透策略探討[J].新課程（小學），2016（1）.

[2]高海兵.淺談如何在小學數學教學中滲透數學思想方法[J].數學學習與研究，2016（12）：53.

[3]馮莉.淺談如何在小學數學課堂中滲透數學思想方法[J].中國校外教育，2017（5）：127.

編輯 王 敏