例談統計圖表的綜合運用
韓賢
[摘要]探尋中考統計圖表的考查形式,分析與解讀統計圖表典例,以培養學生的數據分析意識與應用意識.
[關鍵詞]統計圖表;綜合運用;初中數學
[中圖分類號]G633.6? [文獻標識碼]A? [文章編號]1674-6058(2020)02-0020-02
新課程標準要求讓學生經歷實際問題中收集和處理數據、利用數據分析問題、獲取信息的過程,掌握統計與概率的基礎知識與基本技能.統計圖表就是對實際問題中的數據進行收集、整理與表達,它包括條形統計圖、扇形統計圖、折線統計圖、頻率直方圖和頻率統計表等.在解題中,要求學生正確地識圖、讀圖、畫圖,能提取有用的信息,綜合各方面信息,并通過信息的梳理與觀察發現規律、提出合理化建議等.那么統計圖形有哪些綜合運用呢?
一、扇形統計圖與條形統計圖的綜合運用
當扇形統計圖與條形統計圖結合時,扇形統計圖上會標出各部分所占的百分率,而各部分百分率之和為1,可以利用其他部分的百分率得出所求部分的百分率.在條形統計圖上會標出各部分的具體頻數,而各部分頻數之和等于總數,可以利用其他部分的頻數得到所求部分的頻數,這兩者結合可求得總數.
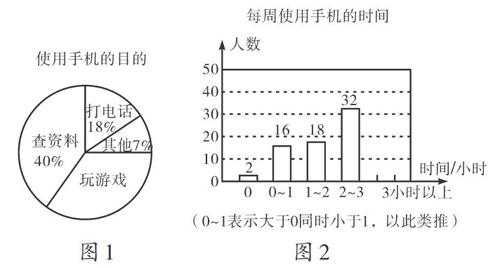
[例1]為了解學生手機使用情況,某學校開展了“手機伴我健康行”主題活動,他們隨機抽取部分學生進行“使用手機目的”和“每周使用手機的時間”的問卷調查,并繪制成如圖1和圖2的統計圖,已知“查資料”的人數是40人.
請你根據以上信息解答下列問題:
(1)在扇形統計圖中,“玩游戲”對應的百分比為??? ,圓心角度數是??? 度;
(2)補全條形統計圖;
(3)該校共有學生2100人,估計每周使用手機時間在2小時以上(不含2小時)的人數.
分析:(1)根據題意,得“玩游戲”對應的百分比為1-(40%+18%+7%)=35%,則“玩
游戲”對應的圓心角度數是360°x35%=126°.
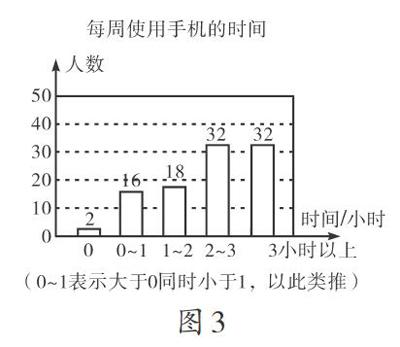
(2)根據題意得40÷40%=100(人),∴玩手機3小時以上的人數為100-(2+16+18+32)=32(人),補全圖形如圖3.
(3)根據題意得2100×{(32+32)/100}(人).
每周使用手機時間在2小時以上(不含2小時)的人數有1344人.
二、折線統計圖與統計表的綜合運用
折線統計圖也標識了各部分的頻數,這一點與條形統計圖相同.不同的是折線統計圖將頻數連起來,使我們可以清楚地看出事物變化的趨勢.統計表一般是指頻數與頻率統計表,從中可以讀出頻數與頻率,頻數與頻率兩者結合可以得出總數及未知頻數與頻率.折線統計圖與統計表結合,可以將統計表的數據在折線統計圖中直觀地顯示出來.
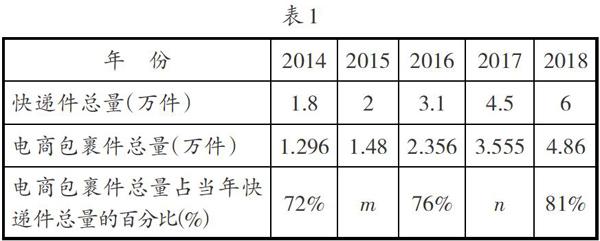
[例2]近年來,隨著電子商務的快速發展,電商包裹件總量占當年快遞件總量的比例逐年增長.根據某快遞公司某網點的數據統計,得到如表1所示的統計表.
(1)直接寫出m,n的值,并在圖4中畫出電商包裹件總量占快遞件總量百分比的折線統計圖;
(2)若2019年該網點快遞件總量預計達到7萬件,請根據圖表信息,估計2019年電商包裹件總量約為多少萬件
分析:(1)m=1.48÷2=74%;n=3.555÷4.5=79%;折線統計圖如圖5所示.
(2)從增長的趨勢看,每年的百分比比上一年增長2%左右,故2019年電商包裹件總量占當年快遞件總量百分比約為83%,2019年電商包裹件總量約為7x83%=5.81(萬件).
三、頻數分布直方圖、頻數分布表與扇形統計圖的綜合運用
頻數分布直方圖與條形統計圖類似,所不同的是頻數分布直方圖橫軸的數據是連續的,而條形統計圖是不連續的,從這兩種圖上都可以獲得各部分的頻數.實際上數據的整理過程,先收集數據,再整理成統計表,繼而根據表達的需要,繪制成直方圖、條形圖、扇形圖或折線圖,所以統計圖的數據來自統計表.
[例3]我市為加強學生的安全意識,組織了全市學生參加安全知識競賽.為了解此次知識競賽成績的情況,隨機抽取了部分參賽學生的成績,整理并制作出如表2和圖6所示的不完整的統計表和統計圖,請根據圖表信息解答以下問題.
(1)一共抽取了??? 個參賽學生的成績;表中a=??? ;
(2)補全頻數分布直方圖;
(3)計算扇形統計圖中“C”對應的圓心角度數;
(4)某校共2000人,安全意識不強的學生(指成績在70分以下)估計有多少人?
分析:(1)總人數=14÷35%=40(人),a=40-8-12-14=6,故答案為40,6;
(2)頻數分布直方圖如圖7所示;
(3)扇形統計圖中“C”對應的圓心角度數=360°×12/40=108°;
(4)200×(6/40)=300(人)安全意識不強的學生(指成績在70分以下)估計有300人.

