圍繞核心素養的空間直角坐標系教學設計

魏安龍

【摘要】本文是蘇教版必修二空間直角坐標系概念課的教學設計，將從教學目標、教學過程中的課前準備、課堂互動的問題設計等方面，圍繞新課程標準的高中數學核心素養進行設計.在教學反思中，聯系高中數學核心素養的每個方面，對教學過程的設計思路、情境設計和課堂教學等方面進行總結反思.

【關鍵詞】空間直角坐標系;核心素養;設計;教學反思

寫教學設計，就需要我們按照教學設計的標準模式走，要有明確的教材分析、學情分析、教學目標、教學重難點，過程方面需要有合理的引入環節，以及最后的目標達成情況分析等.

一、教材分析

在2010年的普通高中數學課程標準中，空間直角坐標系的內容安排在平面解析幾何初步的部分，目的是拓展坐標系的知識，但是這樣的安排弊大于利.所以在2017版的普通高中數學課程標準中，空間直角坐標系的內容就回歸到空間向量與立體幾何部分，這樣能很好地體現學以致用，有利于培養學生直觀想象的核心素養.

二、學情分析

學生在學習這部分知識前，已經理解和掌握了平面直角坐標系的有關知識，對坐標、象限等概念和聯系有了清晰的認識，通過立體幾何初步的學習，已經初步形成空間觀念，具有一定的空間想象能力.

三、教學目標、重難點設計

1.教學目標

空間直角坐標系是在學生具備平面直角坐標系知識，學習了立體幾何初步后的課程，是學生學習空間向量的基礎.依據核心素養的要求，可設計教學目標如下：

（1）通過一維到二維知識結構發展的需要以及笛卡爾故事的具體情境，使學生感受學習空間直角坐標系的必要性;

（2）通過類比聯想，讓學生得出空間直角坐標系的概念，并在此基礎上知道右手系的概念;

（3）結合平面直角坐標系中刻畫點的位置的方法，類比理解在空間直角坐標系中刻畫點的位置的方法;

（4）感受二維平面與三維空間的聯系，能通過類比探索空間直角坐標系中的有關結論.

2.重點與難點

理解空間直角坐標系.

四、課堂教學過程設計

1.課前準備（新課引入）

（1）數軸是怎樣定義的？如何利用數軸確定直線上點的位置？

（2）平面直角坐標系是怎樣定義的？如何利用平面直角坐標系刻畫點的位置？

（3）平面直角坐標系中有哪些重要公式？目前研究了哪些曲線的方程？

（4）情境問題：笛卡爾的故事.

2.課堂互動

問題1：如何定義空間直角坐標系？怎樣畫？

（1）空間直角坐標系的概念，右手直角坐標系（見教材）.

（2）空間直角坐標系的畫法，空間點的坐標表示（見教材）.

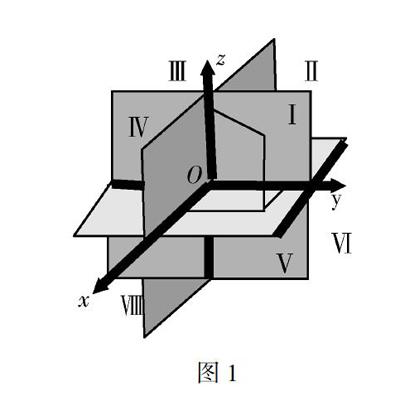
（3）空間直角坐標系中區域的劃分（如圖1），三個坐標平面把空間分成八個部分，即八個卦限，每一部分稱為一個卦限.

問題2：空間直角坐標系中怎樣畫點？

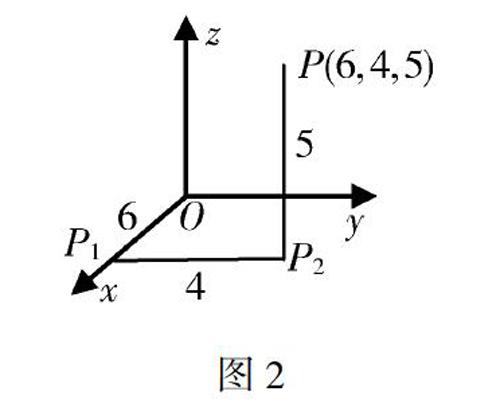
例1 在空間直角坐標系中，畫出點P（6，4，5）.

分析 在空間直角坐標系中畫出點P，可按下列步驟進行操作：

解 作空間直角坐標系O-xyz，并在圖中作出點P1（6，0，0），

P2（6，4，0），最后得出點P（6，4，5） 如圖2所示.

例2 在長方體ABCD-A1B1C1D1中，AB=10，AD=8，AA1=6.若以點A為坐標原點，以射線AB，AD，AA1分別為x軸、y軸、z軸的正半軸建立空間直角坐標系，試求這個長方體各個頂點的坐標.

解 據題意，可得A（0，0，0），B（10，0，0），C（10，8，0），D（0，8，0），

A1（0，0，6），B1（10，0，6），C1（10，8，6），D1（0，8，6）.

例3 （1）在空間直角坐標系O-xyz中，分別畫出三個不共線的點A，B，C，并且使這三個點的坐標都滿足z=4，畫出圖形;

（2）寫出由A，B，C這三個點確定的平面內的點的坐標應滿足的條件.

解 （1）取三個點分別為A（0，0，4），B（5，0，4），C（0，5，4），如圖3.

（2）因為A，B，C三點不共線，因此它們可以確定平面ABC，平面ABC上點的坐標都滿足z=4，如圖3.

問題3：二維平面中的結論在三維空間中推廣可以得出哪些結論？（見下表）

例4 試求點A（2，-1，-3）關于空間直角坐標系中xOy平面、zOx平面及原點的對稱點.

解 點A（2，-1，-3）關于xOy平面的對稱點為A1（2，-1，3），關于zOx平面的對稱點為A2（2，1，-3），關于原點的對稱點為A（-2，1，3）.

問題4：本節課你學習了哪些知識？學會了解決哪些問題？

經學生總結后繪制思維導圖（如圖4）.

3.課后作業（略）

五、教學目標達成及教學反思

空間直角坐標系一課的設計，總體想法是參考老教材、老課標，圍繞新課標、新高考進行設計，圍繞核心素養開展教學.

1.目標達成分析

根據學生的課堂反應以及作業完成的準確程度分析，本節課能很好地達到既定的教學目標，特別是數學抽象函數與直觀想象的核心素養得到了進一步培養.

2.本節課的教學設計思路

新課程標準提出的“數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析[2]”等核心素養是本節課設計的主要線索.

（1）圍繞核心素養的教學目標的確定.重點圍繞邏輯推理、數學抽象兩方面進行目標的制訂（見教學目標）.

（2）圍繞核心素養開展的課堂情境設計.本節課有兩個情境，一個是從數學研究的坐標發展方面，另一個是笛卡爾的故事.在這個過程中，滲透了數學抽象、邏輯推理、數學建模、直觀想象的核心素養.

（3）以類比推理為主線發展核心素養，以空間直觀想象為重點，以數學抽象、數學建模問題為課堂互動.本課以設計問題串的形式，引導學生提出、分析、解決問題，在問題解決的過程中滲透核心素養.

（4）利用不同的教學手段和展示，提高教學效果，將核心素養的要求落到實處.教師規范的板書是對學生潛移默化的影響.思維導圖的設計與呈現是引導學生知識升華、思維能力提高的重要手段.本節課的板書設計主要有三個區域：例題演示區，重點內容呈現區，臨時板書區.重點是思維導圖的設計，它發展了學生的抽象概括水平和邏輯推理能力.

3.不足與存在的問題

對照“高效課堂操作指南”，對照新課程標準教學建議中的落實“四基”、培養“四能”（基礎知識、基本技能、基本思想、基本活動經驗簡稱“四基”，提高從數學角度發現和提出問題的能力、分析和解決問題的能力簡稱“四能”）的要求，以及新課程標準教學建議中“教學目標的制訂要突出數學學科核心素養;情境創設和問題設計要有利于發展數學學科核心素養;整體把握教學內容，促進數學學科核心素養的連續性和階段性發展;既要重視教，更要重視學，促進學生學會學習”的相關內容，本節課有以下不足：

（1）概念的呈現速度快，剖析膚淺，留給學生鞏固思考的空間有限;

（2）教師的規范給了學生潛移默化的影響，但也可能框住學生的思維，有形的影響不如無痕的滲透;

（3）需要進一步提高數學修養，廣泛且深入地開展理想教育，加強核心素養在每一個知識點方面的修煉和理解.

【參考文獻】

[1]單墫.普通高中課程標準實驗教科書數學：必修2[M].南京：鳳凰教育出版社，2012.

[2]中華人民共和國教育部.普通高中數學課程標準[M].北京：人民教育出版社，2018.