高中數學教學設計——“導數的概念”

張志偉

摘要：本節課程教學目標為：經歷從生活中的變化率問題抽象概括出平均變化率的過程，體會數學知識來源于生活，又服務于生活，體會數學概念形成的“歸納——演繹”的模式；了解瞬時速度、瞬時變化率的概念；理解導數的概念，知道瞬時變化率就是導數，體會導數的思想及其內涵；會求函數在某點處的導數，通過動手計算培養學生觀察、分析、比較和抽象概括的能力；體會“逼近”的思想方法。

關鍵詞：高中數學；教學設計；導數

中圖分類號：G633.6文獻標識碼：A文章編號：1992-7711（2020）10-0164

本節課是對“人教B版《普通高中課程標準實驗教科書——數學選修1-1》第三章第一節3·1·2的第一課時——導數的概念”的教學。導數是微積分的核心概念之一，它是研究函數增減、變化快慢、最大（小）值等問題的最一般、最有效的工具。考慮到高中學生認知水平有限，沒有采用一般的“數列——數列的極限——函數的極限——導數”這種建立概念的方式，而是從變化率入手，用形象直觀的“逼近”定義導數。這樣一來，一方面排除了因難以理解極限的形式化定義，而對導數本質理解的干擾，將更多的精力放在對導數本質與內涵的理解上。另一方面，學生對逼近的思想有了豐富的直觀基礎和一定理解，有利于大學學習嚴格的極限定義。本節課將導數概念的建立劃分為兩個階段，首先明確瞬時速度和切線斜率的含義，然后去掉物理背景和幾何背景，由兩個實例出發，抽象出一般函數的瞬時變化率的概念，給出導數的定義。借助信息技術，通過讓學生親自計算、幾何畫板展示等方法，讓學生體會逼近的思想和用已知探求未知的思考方法。基于以上分析，確定本節課教學重點為：建立導數概念及對導數思想和內涵的理解。

一、教學目標設置

本節的中心任務是形成導數概念，概念形成需要通過兩個實例抽象得出。1.借助高臺跳水問題，明確瞬時速度的含義；2.借助拋物線的割線逼近切線的問題，明確切線斜率的含義；3.以速度模型為出發點，結合切線斜率抽象出導數概念，使學生認識到導數就是瞬時變化率，理解導數的內涵；4.通過平均變化率的計算，讓學生切身體會逼近思想，滲透以已知探求未知的思考方法，提升數據處理和數學抽象的核心素養。

二、教學過程設計

1.知識回顧

2.設疑自探

如何求運動員的瞬時速度？與平均速度有什么關系？引起學生思考。我們可以用來研究高臺跳水運動員在某時刻的瞬時速度。師生共同確定想法：計算t=2附近的平均速度，細致地觀察它的變化情況。

3.解疑合探

下表是計算問題1中當t=2秒處附近時間段內平均速度的表格，請分組合作完成此表，猜想在t=2秒處的瞬時速度，并說明理由。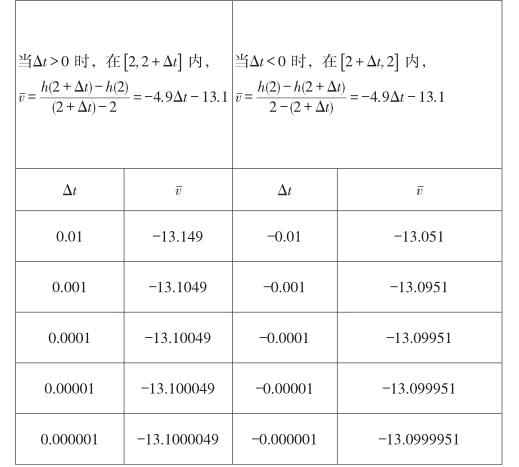

為便于觀察變化趨勢，要計算一組平均速度，引導學生采用數學符號將想法具體化，明確計算公式。要求學生分組合作，通過學生親自計算引導他們發現平均速度的變化趨勢。

（2）當Δt趨近于0時，平均速度vˉ有什么樣的變化趨勢？

結合學生的計算結果，組織學生觀察、討論平均速度的變化趨勢，引導學生說出“當Δt趨近于0時，平均速度趨近于一個確定的值-13.1”。

（3）更多數據，感受規律

我們用這個方法得到了高臺跳水運動員在t=2s附近，平均速度逼近一個確定的常數。那其他時刻呢？比如t=1s？請大家按照剛才我們探究t=2s時的過程，用同樣的方法，計算t=1s時刻附近的平均速度。

4.總結規律

運動員在某一時刻t0的瞬時速度怎樣表示？已知其他路程和時間函數的解析式，求瞬時速度都是這樣嗎？

帶領學生回顧探求t=2時瞬時速度的全過程，引導學生從特殊到一般，獲得t=t0時瞬時速度的形式化表示。教師介紹符號，并解釋符號含義。

總之，教師可以引導學生從兩個方面進行小結。知識方面：瞬時速度，切線斜率，瞬時變化率，即導數的定義。思想方法：思考方法——以已知探求未知，特殊到一般，具體到抽象，逼近思想。

（作者單位：內蒙古師范大學附屬學校011517）