兒童哲學視野下質疑能力的培養

何佳

摘要：質疑能力低下已經成為中國學生素養的一個缺陷。究其原因，傳統的教學模式使學生的思維形成了定式，嚴重制約了學生思維的發展。基于兒童哲學視野，結合數學實驗教學案例，從實踐層面進行策略架構，在實驗課中通過鼓勵、批判、問學等方式培養學生的質疑能力。

關鍵詞：兒童哲學;質疑能力;小學數學實驗教學

20世紀70年代，美國著名哲學家李普曼創建了“兒童哲學”，其主要的意義是為兒童提供哲學訓練，使兒童學會像哲學家那樣思考，從日常思維轉向反思性思維，從不假思索轉向深思熟慮，從常規思維走向批判性思維[1]。《義務教育數學課程標準（2011 年版）》也明確指出教師要經常思考“如何引導學生善于與同伴合作交流，既能理解、尊重他人的意見，又能獨立思考、大膽質疑”[2]。

基于兒童哲學和課程標準的要求，我們這樣理解質疑能力：學生在認知活動中，對意識到的一些難以解決的、感到疑惑的實際問題，能主動產生懷疑、困惑、焦慮、探究等心理狀態的能力。質疑的產生是探索的開始，它有利于培養學生追求科學的精神，有利于發揮學生的創造思維能力。在小學數學教學中培養學生質疑的習慣和能力，是全面推進創新教育的開端，是培養創新型人才的關鍵[3]。

那么，在具體的數學實驗教學中，如何培養學生的質疑能力呢？為此，我們有必要作一些探討和實踐。

一、鼓勵：為質疑能力的萌發提供土壤

（一）放飛兒童心靈，細心呵護質疑意識的生發

在日常課堂教學中，時常有學生冒出令人意想不到的質疑發問。如果教師以成人的眼光看學生，那么學生的很多新穎奇特的質疑都可能被忽視，長此以往，學生便會將心中的質疑放在頭腦里，不愿將它提出來。

要改變學生這種害怕質疑的現狀，就必須創建和諧的師生關系。“放飛兒童心靈”，不是說說而已，而應落到實處。教師要在心靈深處平視學生，用“兒童的大腦”去思考，用“兒童的眼光”去看待，用“兒童的情感”去體驗……真正站到學生那邊去，走進學生的世界，認真傾聽，細心體會，做一個欣賞者、引導者和保護者，鼓勵并善待學生的質疑發問，讓學生在溫馨的課堂中，體驗數學學習的快樂和美好。

（二）善待兒童過錯，用心保護質疑因子的生長

德國哲學家黑格爾指出，錯誤本身乃是“達到真理的一個必然的環節”[4]。無論學生提出的質疑有無價值，我們教師首先需要做的是對這種質疑行為給予充分的肯定，然后從學生的質疑中找到積極、合理的因素，從而增強學生質疑問難的勇氣和興趣。

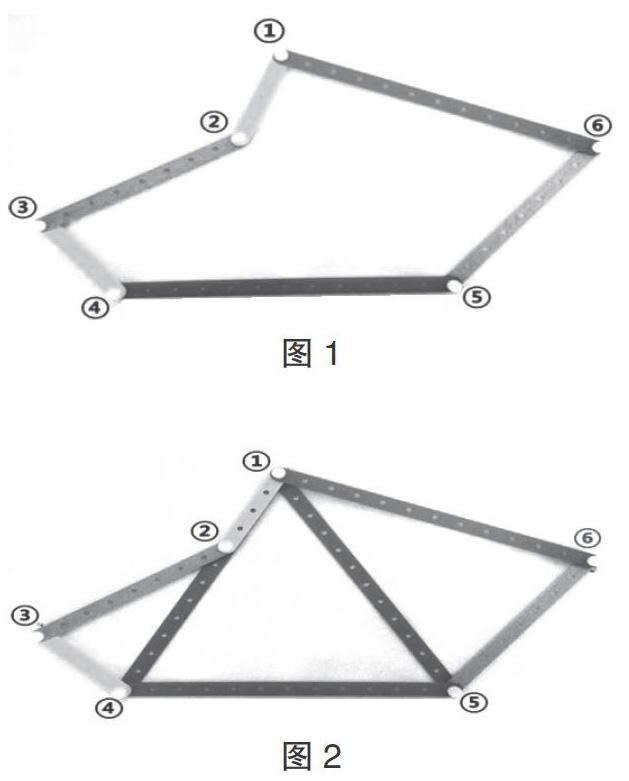
依托蘇教版數學教材四年級下冊中的“你知道嗎”，筆者執教了一堂檢驗性數學實驗課“三角形的穩定性”。在提出“如果要使六邊形不變形，至少需要加上幾根拼接條？”這一問題后，筆者讓學生先猜想，然后動手驗證。匯報時，學生們紛紛拿著“成功”的作品向全班同學展示，結果都是“至少需要加上3根拼接條”。正當筆者準備下結論時，“意外”出現了。一位學生舉手示意自己找到了反例。懷著忐忑的心情，筆者請他說說自己的想法和做法。只見這位學生拿著“反例”充滿自信地跑上講臺，邊講邊演示：“這是一個六邊形（如圖1），用一根拼接條連接頂點①和⑤，再用一根拼接條連接頂點①、②、④，像這樣添加兩根拼接條（如圖2），就能使這個六邊形不變形……”全場啞然。筆者在一旁，從“驚嚇”到“驚喜”，首先肯定了這位學生敢于質疑的勇氣，然后啟發全班學生“這到底是不是一個反例呢？”通過全班的探討，大家發現添加的第2根拼接條與原來六邊形的一條邊重合了，重合的那條邊也相當于是添加了一根拼接條，因此這并不是一個“反例”，而恰恰再一次驗證了“六邊形至少需要添加3根拼接條才能使它不變形”這一結論的正確性。

教師要從科學的角度理解學生的各種差錯，要肯定他們敢于質疑的勇氣，評價在對錯之外，重在激勵學生探究。如此，在課堂上學生才敢于發表自己的意見，教師才能聽到學生思維的真實的聲音。

（三）激發兒童思考，精心守護質疑精神的生成

學源于思，思起于疑。蘇霍姆林斯基說：“教學的技巧并不在于能預見課堂所有的細節，而在于根據當時的情況，巧妙地在學生不知不覺中做出相應的變動。”[5]教學中要因勢利導，在學生有疑問，正要提出質疑而苦于不知道怎樣表達的時候，真正做到想學生之所想，幫助學生理清思路，明確方向，推動思維的發展，讓課堂教學在適時調控中推進。

在蘇教版數學教材六年級上冊“分數乘整數”的教學中，筆者采用數學實驗開展教學，首先直接提出問題：“如果用（b≠0）表示分數，用n表示整數，憑直覺，大膽猜想一下，你認為像這樣的分數乘整數，可以怎樣計算？”引發學生提出三種猜想：

對這些猜想，筆者給予了充分贊賞和肯定。此時，有部分學生緊鎖眉頭，似乎對某個猜想感覺很困惑。于是，筆者便順水推舟，提出問題：這三種猜想都需要一一驗證嗎？這時緊鎖眉頭的學生一下興奮了起來，提出質疑：“猜想①肯定不合理，因為根據分數的基本性質，等式右邊還是等于，跟左邊不相等。”緊接著，便又有學生質疑：“我覺得猜想③也不合理，根據乘法的意義，等式左邊×n表示n個相加，和應該大于，而等式的右邊明顯小于。”兩位學生的質疑贏得了全班學生的熱烈掌聲。正是因為有了這樣的質疑和推想，接下來學生們只需綜合運用舉例驗證、反例求證、演繹推理等方法來驗證猜想②是否合理。如此基于課堂生成理念下的課堂教學，煥發了從未有過的生機和活力，一課下來，令筆者感動不已。課堂之所以是充滿生命活力的，就因為學生不再是按部就班，被教師牽著走，而是在平等、自由、真誠的對話場景中敢于猜想、質疑，勇于探究、實踐。

二、批判：為質疑能力的生長撒下良種

（一）轉變，讓兒童從“看客”走向“創客”

數學學習中，以節約時間提高效率為由，許多課堂都是以教師的講解演示居多，學生扮演的大多是看客，沒有真正親身經歷數學學習的完整過程，因此便沒有了內心真切的想法，質疑能力也就慢慢消退了。而數學實驗則是以學生的個別學習為基礎的一種學習方式，學生能全員、全程參與到探索和研究活動中去[6]。學生經歷知識的再創造，有了深切的體驗和感受，對于與自己不同的想法自然便能提出自己獨特的見解。

教學“三角形的穩定性”，筆者為每個學生準備了實驗所需的工具——拼接條，并且通過開展序列化的實驗活動，讓學生通過猜一猜、圍一圍、比一比、拉一拉、說一說等環節，數學化地經歷三角形穩定性的建構過程，幫助學生經歷數學知識發生、發展的過程，形成自身對此內容的個性化理解。探討如何在不改變四邊形四條邊的情況下使得四邊形不變形時，聯系三角形的穩定性，學生容易想到添加一根拼接條分出一個三角形，便可以使四邊形不變形;但個別學生在實際操作中提出質疑：添加一根拼接條將原來的四邊形分成了兩個四邊形后，也“拉”不動（如圖3）。這一質疑聲引起了全班學生的熱烈討論和深入思考。一石激起千層浪，因為一個特例，激發一群學生的好奇心和探究欲，帶動了學生“疑中精進”……在這樣的數學實驗課堂中，學生儼然從問題的看客變成新知探索的創客。

（二）逆襲，讓兒童從“習慣”走向“反思”

習慣性思維是根據自己的經驗形成某些結論。教師培養學生的質疑能力，首先要改變學生的思維習慣。教學蘇教版數學教材六年級上冊“動手做”中的內容——“長方形面積的變化”時，筆者提出“如果長方形的長增加，寬減少，面積會有怎樣的變化呢？”大部分學生看到一個量增加，另一個量減少，不假思索地認為面積不變。靜靜等待15秒后，一個學生提出質疑：“面積變了，雖然分率都是，但是它們的單位‘1不相同。我們可以通過數學實驗來解決這個問題。”果然，學生們通過畫圖、大量舉例、用字母推理、利用數學模型等（如圖4）進行分析后，發現面積減少了。

（三）生發，讓兒童從“定式”走向“發散”

教學的主要任務不是積累知識，而是發展思維。在日常教學中，師生都容易形成一套固定的考慮問題的模式和與之相適應的經驗，即思維定式。思維定式有時會禁錮思維，造成思維的惰性，成為質疑能力最大的障礙。教師應鼓勵學生靈活調整原來的思維方式，改變思考問題的角度和方向，按照不同的思路來分析、解決問題。

在教學蘇教版數學教材三年級下冊“長方形和正方形面積的計算”時，其中有一個環節：正方形的面積可以怎樣計算？學生思考后，一般會呈現這樣的方法：用邊長1厘米的小正方形鋪滿正方形（如圖5①）。教師在肯定學生的這種方法后，順勢提出質疑：“有的學生準備的小正方形比較少，鋪不滿怎么辦呢？”立馬有學生想到：用邊長1厘米的小正方形鋪一行和一列，就能知道每行有幾個，有幾行，同樣能得出正方形的面積（如圖5②）。還有學生提出：“我沒有用小正方形去鋪，也可以得出正方形的面積計算公式，我是依據‘正方形是特殊的長方形直接推理證明的（如圖5③）”……看似不經意的質疑讓學生的思維變得活躍，有效地訓練了學生的發散思維。教師以實驗的方式，讓學生在親自經歷實驗的過程中，真實體驗知識的產生和形成過程。

三、問學：為質疑能力的成熟續足養分

培養學生的問題意識是學生形成質疑能力的前提和基礎。教師要鼓勵學生敢于提問，善于提問，激勵學生因問而學、善問而學，從而達到問學合一。

（一）引導“善問而學”，在實驗中質疑和反思

《禮記》中指出：“善問者如攻堅木：先其易者，后其節目;及其久也，相說以解。不善問者反此。”[7]培養學生的問題意識是學生形成質疑能力的前提。教師的教學設計不僅要考慮自己教得方便、教得精彩、教得舒暢，而且要更多地思考學生如何“學”，突出學生自己提出問題、解決問題的過程，課堂教學的順暢性在動態生成的互動學習中真實發生。

教學蘇教版數學教材六年級上冊“長方體的體積”這一課時，筆者確立了“立足于學生的已知，激發起學生靈動的思維”的教學追求，讓學生知無不言，言無不盡。大部分學生在學之前就已經知道了長方體體積的計算公式，但少數學生很困惑，提出質疑：“為什么長方體的體積等于長乘寬乘高呢？”這一問題催生了學生有價值的探究。接著根據大部分學生初步探究的困惑狀況，教師指點迷津：“我們能不能運用實物進行操作呢？”，讓學生在實驗中自求自得。通過實驗，學生各抒己見。觀點在碰撞，智慧在飛揚，對體積公式的理解步步深入。在質疑和反思中，學生們的操作能力、思辨能力、表達能力都得到了提高。整個實驗活動過程本質上是一個引導學生不斷克服困難，經歷自主探索，形成良好思維品質的過程。

（二）提倡“刨根問底”，在實驗中推演和論證

李普曼認為，兒童帶著強烈的好奇心和求知欲進入學校，而這種好奇心和求知欲在隨后的學校生活中消失殆盡，這是傳統教育的結果[8]。作為教師，我們要充分開發兒童身上的潛質，鼓勵他們不斷質疑答疑，刨根問底，教會他們思維。

教學分數加減法練習時，有這樣一個題組：

學生通過觀察、計算，不難發現：分子是1，分母只有公因數1的兩個分數相加減，得數的分母是兩個分母的積，分子是兩個分母的和或差。教學在這便結束了嗎？不！這只是根據4個例子得出的一個猜想，還需要進一步的驗證。學生舉了大量的例子，發現都符合猜想。這時教師引導學生質疑：例子舉得完嗎？能分別用一個式子來表示這里的加法和減法嗎？學生容易想到用字母來表示：+=（a， b）=1和-=（a， b）=1。教學到這可以結束了吧？不！“知其然，知其所以然。”筆者引導學生提出質疑：“為什么這類特殊的分數加減法能得到這么有意思的結果呢？”通過思考、推演，學生很快能聯系分數加減法的計算法則進行論證：+=+=（a， b）=1、-=-=（a， b）=1。其實，這類特殊分數的分母的最小公倍數就是它們的乘積，也就是說公分母是它們的乘積，所以分母為兩數之積，分子為兩數之和或之差。不完全歸納法得出的結論不一定正確，這里“刨根問底”，深入挖掘規律的內在緣由，不僅僅停留在合情推理的層面上，而是讓學生聯系計算法則，進行演繹推理，證明猜想一定是正確的，從而得出結論。

現代教育家陶行知說：“發明千千萬，起點是一問。”[9]只有“問了”，才能深入思考;只有深入思考了，才能不斷產生問題……這樣，學生的學習能力、探究能力就在“質疑—答疑—再質疑—再答疑”的循環往復中不斷提高。

（三）鼓勵“標新立異”，在實驗中超越和創造

創新精神和創新能力是可以通過教育來完成的，而質疑能力是創新的前提和內核。數學實驗教學中，我們教師除了要培養學生的質疑能力和精神，還要創造機會，激發并最大限度地挖掘學生身上的創造潛能，鼓勵他們“天馬行空”的想法，放飛他們的“奇思妙想”。

筆者在教學蘇教版數學教材六年級下冊“大樹有多高”時，直接拋出問題“我們學校的教學樓有多高？”課前預習過的學生立馬回答：“可以利用教學樓的高度與其影子之間的關系來解決這個問題。”其他學生默認。這個問題本身沒有唯一正確的答案，筆者鼓勵學生質疑、思辨，令人意想不到的是，學生想到了很多其他的辦法：將每一層樓的高度測量出來后相加;打電話詢問建造大樓的設計師;爬到樓頂，然后放卷尺下來測量;放個氫氣球上去，到樓頂時給繩子做上標記，再拉下來量一量……學生的想法獨特且有創意，不再被教材中的唯一解法所束縛。實踐證明，讓學生學會像數學家那樣去思考、去表達，能真正激發他們的創造潛能，發展他們的質疑能力。

在數學學習中保有一顆鮮活敏感的心靈，不斷追問下去，問題就會層出不窮，創新也會連續不斷。

參考文獻：

[1]華堂生.兒童哲學的內涵及其哲學預設[J].學前教育研究， 2014（6）：45.

[2]中華人民共和國教育部.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社， 2011：48.

[3]陳書芳.淺析小學生數學質疑能力的培養[J].亞太教育， 2015（8）：18.

[4]錢燕.借“錯”發揮 精彩紛呈[J].小學教學參考，2018（5）：70.

[5]蘇霍姆林斯基.給教師的建議[M].杜殿坤，譯.北京：教育科學出版社， 1984：222.

[6]張輝.數學實驗：小學數學教學的新視界[J].江蘇教育， 2015（17）：36.

[7]樂正克.學記[M].高時良，譯.北京：人民教育出版社， 2016：6.

[8]郅庭瑾.為何而教——超越知識與思維之爭[D].上海：華東師范大學， 2001：90.

[9]周魯輝.生本課堂模式下小學英語課堂提問的有效設計[J].中國校外教育， 2019（7）：84.

責任編輯：石萍