基于隨機森林的數學試題難易度分類研究

梁瓊芳 莎仁

摘 要：為了實現教育領域的“個性化”，無論是自由組卷的個性化，還是試題推薦的個性化，都首先需要確定試題難易度。研究目標為尋找新的方法解決基于試題難易度的分類問題，提高分類準確率。以高中數學為例，采用2018年多套高考數學試題作為實驗數據，對原始數據各個特征進行相關性分析，剔除影響較小的特征，再采用隨機森林算法探索試題難易度分類問題，對參數進行改進優化，并與其它分類方法進行對比。實驗結果證明，采用隨機森林的高中數學試題分類準確率高達90%，而其它3種分類算法準確率分別為72%、74%、74%。因此得出結論，隨機森林算法在高中數學試題難易度分類上有較好表現，能夠大幅提高分類準確率。

關鍵詞：高中數學;試題難易度;分類算法;決策樹;隨機森林

DOI：10. 11907/rjdk. 191358 開放科學（資源服務）標識碼（OSID）：

中圖分類號：TP301文獻標識碼：A 文章編號：1672-7800（2020）002-0122-05

英標：Classification of Mathematics Testability Difficulty Based on Random Forest

英作：LIANG Qiong-fang， SHA Ren

英單：（School of Information Science & Technology， Northeast Normal University， Changchun 130117，China）

Abstract： In order to realize individualization in the field of education， whether it is the individualization of the free test papers or the personalization of the test questions， the difficulty of the test questions must firstly be determined. Therefore， the research goal of this paper is to find new ways to solve the test questions. The classification problem of difficulty is easy， and the accuracy of classification is improved. Taking high school mathematics as an example， in this paper， the mathematics test questions of the college entrance examination in 2018 are used as experimental data， and the correlation analysis of each feature of the original data is carried out to eliminate the features with less influence. Then the random forest algorithm is used to explore the difficulty classification of the test questions， and the parameters are improved and optimized and compared with other classification methods. Experiments show that the accuracy rate of random forests for high school mathematics test classification is as high as 90%， while the accuracy of other classification algorithms is 72% and 74%. Therefore， it is concluded that the random forest algorithm has excellent performance in the classification of high school mathematics questions and can greatly improve the classification accuracy.

Key Words： high school mathematics; test difficulty; classification algorithm; decision tree; random forest

0 引言

近年來，個性化推薦技術正在各個領域迅速興起，而教育領域作為當今社會必不可少且不容忽視的一部分，越來越需要“個性化”的引入。如今網絡試題題庫、組卷系統層出不窮，都是為了實現學生的高效練習，而確定試題難易程度是題庫構建，以及自由組卷與試題個性化推薦的基礎。

在數學試題難易度研究方面，國外Pollitt等[1]在1985年提出難度的3個來源，1996年劍橋考試委員會研究者[2]從權威角度提出影響數學試題難易度的因素，1999年Ahmed等[3]研究了試題認知要求程度對問題難度的影響，直至2006年Leong[4]歸納了影響試卷難度的4個因素，分別為內容、材料、主體因素與命題者決策。在國內，1994年任子朝等[5]提出可從多個客觀角度評估試題難度;2002年李紅松等[6]提出試題難易度與學生成績分布有關，并采用主觀模糊評價方法結合成績分布確定試題難易度;2008年，教育部考試中心[7]歸納總結了影響試題難易度的因素，包括知識點個數、運算過程步驟數、推理轉折數、設陷數、創新度、繁瑣度、啟發度、猜測度等;2016年，候飛飛[8]根據試題自身特點，結合C4.5決策樹方法，對物理試題進行難易程度分類研究，驗證了決策樹分類算法的可行性;2018年，陳薈慧等[9]進行基于在線測評系統的編程題目難度研究，但仍然依賴于被試的作答通過率;同年曹開奉等[10]總結歸納了我國高考理科試題難度影響因素，為本文研究打下了基礎。本文致力于實現高中數學試題的客觀難易度分類，以避免通過人為主觀判斷或過分依賴于被試作答通過率進行難易度分類造成的偏差。

常用分類算法如下：典型的樸素貝葉斯方法，針對大量數據訓練速度較快，并支持增量式訓練，對結果的解釋便于理解，但在大數據集下才能獲得較為準確的分類結果，且忽略了數據各屬性值之間的關聯性[11];K-最近鄰分類算法比較簡單，訓練過程迅速，抗噪聲能力強，新數據可以直接加入訓練集而不必重新進行訓練，但在樣本不平衡時結果偏差較大，且每次分類都需要重新進行一次全局運算[12];決策樹分類算法易于理解與解釋，可進行可視化分析，運行速度較快，可擴展應用于大型數據庫中，但容易出現過擬合問題，且易忽略數據屬性間的關聯性[13]。

自2000年以來，深度學習等人工智能技術得到了迅速發展，在很多領域都取得了較好的應用效果。其中隨機森林算法在分類方面表現突出，其避免了決策樹分類算法中容易出現的過擬合問題，并在運算量未顯著增加的前提下，提高了分類準確率[14]。因此，本文旨在利用隨機森林算法實現一種更精確、客觀的試題難易度分類方法，既能節省人力，又可提升分類準確率與客觀性。

1 隨機森林

1.1 決策樹——隨機森林的基分類器

決策樹作為隨機森林的基分類器，是一種單分類器的分類技術，也是一種無參有監督的機器學習算法[15]。決策樹可視為一個樹狀模型，由節點與有向邊組成，其中包括3種節點：根節點、中間節點和葉子節點。決策樹構建不需要先驗知識，并且比諸如神經網絡的方法更容易解釋。決策樹分類思想實際上是一個數據挖掘過程，其通過產生一系列規則，然后基于這些規則進行數據分析。構建決策樹的一個關鍵問題是節點分裂特征選擇，由于不同分裂標準對決策樹的泛化誤差有很大影響，因此根據不同劃分標準，學者們提出了大量決策樹算法[16]。

其中Hunt等[17]提出的CLS算法隨機選擇分裂節點，Quinlan等[18]提出的ID3算法基于信息嫡，C4.5算法基于信息增益率[19]，Breiman等[20]提出的CART算法基于Gini指標，然而沒有一種算法在各種數據集上都能得到最好結果。決策樹采用單一決策方式，因此具有以下缺點：一是包含復雜的分類規則，一般需要決策樹事前剪枝或事后剪枝;二是收斂過程中容易出現局部最優解;三是因決策樹過于復雜，容易出現過擬合問題。

1.2 隨機森林構建

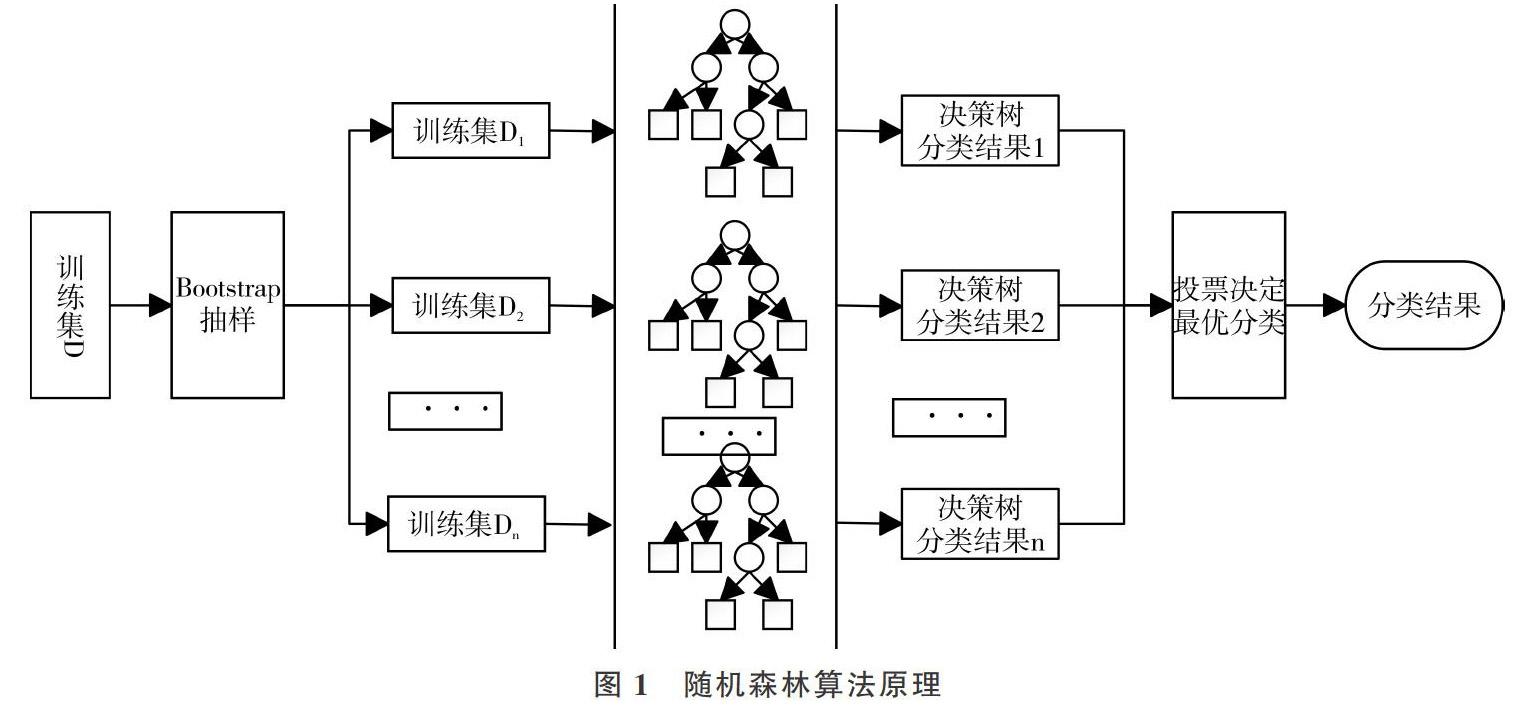
為了克服以上所述決策樹算法的不足，結合集成學習思想[21]，研究者們提出了“森林”的概念。森林中的決策樹按照一定精度進行分類，最后所有決策樹參與投票決定最終分類結果，這是隨機森林的核心概念。隨機森林構建主要包括以下3個步驟：

（1）為N棵決策樹抽樣產生N個訓練集。 每一棵決策樹都對應一個訓練集，主要采用Bagging抽樣方法從原始數據集中產生N個訓練子集。Bagging抽樣方法是無權重的隨機有放回抽樣，在每次抽取樣本時，原數據集大小不變，但在提取的樣本集中會有一些重復，以避免隨機森林決策樹中出現局部最優解問題[22]。

（2）決策樹構建。該算法為每個訓練子集構造單獨的決策樹，最終形成N棵決策樹以形成“森林”。節點分裂原則一般采用CART算法或C4. 5算法，在隨機森林算法中，并非所有屬性都參與節點分裂指標計算，而是在所有屬性中隨機選擇某幾個屬性，選中的屬性個數稱為隨機特征變量。隨機特征變量的引入是為了使每棵決策樹相互獨立，減少彼此之間的關聯性，同時提升每棵決策樹的分類準確性，從而提高整個森林的性能。

（3）森林形成及算法執行。重復步驟（1）、（2），構建大量決策樹，形成隨機森林。算法最終輸出由多數投票方法實現。將測試集樣本輸入隨機構建的N棵決策子樹進行分類，總結每棵決策樹分類結果，并將具有最大投票數的分類結果作為算法最終輸出結果。

隨機森林算法原理如圖1所示。

2 基于隨機森林的試題難易度分類模型構建及優化

2.1 數據特征分析與選擇

本文采用的試題數據為2018年全國各省高考數學試題，部分試題特征來源于組卷網，但其涵蓋的試題特征不夠全面，故其它影響難易度的試題特征可通過對答案的解析加以確定，并自主進行數據標記，主要字段說明見表1。

（1）無關數據剔除。表1中序1、2、3、5特征對試題難易度分類沒有價值，不作為訓練特性，故刪除該字段。

（2）對連續性變量，采用Pearson（皮爾森）相關系數方法驗證與試題難易度值相關關系是否顯著[23]，屬性中連續變量有textLength和guessMeasure，其與難度值的Pearson相關性系數分別為0.325 031和-0.095 424，故保留textLength，刪除guessMeasure。

（3）對于二分類變量，采用點二列相關系數方法驗證與試題難易度值相關關系是否顯著[24]，特征中二分變量與難易度的點二列相關系數分別為type0.295 424、knowledgePos-0.149 294、conditionSatisfact-0.442 642、expressionWay-0.011 241和inspireMeasure0.011 241，故只保留type與conditionSatisfact特征，刪除其它特征。

（4）對于等級變量，采用Spearman（斯皮爾曼）等級相關系數方法驗證與試題難易度值相關關系是否顯著[25]，特征中等級變量與難易度Spearman相關系數分別為knowledgeNum0.460 722、backgroundLevel0.266 939、solveStep 0.580 002、physicalLevel0.587 000、mathLevel0.514 686、moduleNum0.406 973、thinkingWay0.066 568和novelMeasure0.130 309，刪除thinkingWay與novelMeasure特征，保留其它特征。

綜上，最終選擇影響試題難易度的9個特征。采用隨機森林算法作特征選擇，可以很好地解決過擬合問題，同時也能過濾掉重要性很低的特征，提高模型分類準確率。

2.2 模型構建與優化

采用CART 算法作為隨機森林構建決策樹的方法，采用Gini系數最小準則進行節點分裂。CART 算法在訓練過程中需要計算每個屬性的Gini指標，并選擇一個具有最小Gini指標的變量對當前節點進行分裂，通過遞歸形式構建決策樹，直至達到停止條件。Gini系數計算公式如下：

式（1）中K表示有K個類別，[pmk]表示節點m中類別k所占比例，當Gini取最小值0時，此時數據類別最純;當Gini取最大值1時，則表示當前節點的數據類別不同。根據式（1）計算特征的Gini系數，將Gini值最小的點作為該層分裂節點，遞歸地構建決策樹。重復上述步驟，形成隨機森林。構建過程中各特征重要性見表2。

對隨機森林的minimal node size與mtry進行參數尋優，最終確定構建的最優隨機森林node size為33，mtry為4。其中minimal node size尋優過程中測試集分類準確率變化見圖2。

3 實驗與分析

3.1 實驗設計

實驗分為兩個階段：模型訓練階段與測試階段。將數據集按7∶3的比例劃分為訓練集和測試集，分別利用樸素貝葉斯分類、KNN分類、決策樹分類以及本文構建的隨機森林方法進行分類預測實驗，并將不同算法的混淆矩陣指標及準確率Accuracy進行對比[26]。

3.2 實驗結果

KNN分類算法中，neighbors值變化與最終分類準確率關系變化見圖3，故最終選用5-nearest neighbor model模型。

4種分類算法實驗結果見表3、表4。

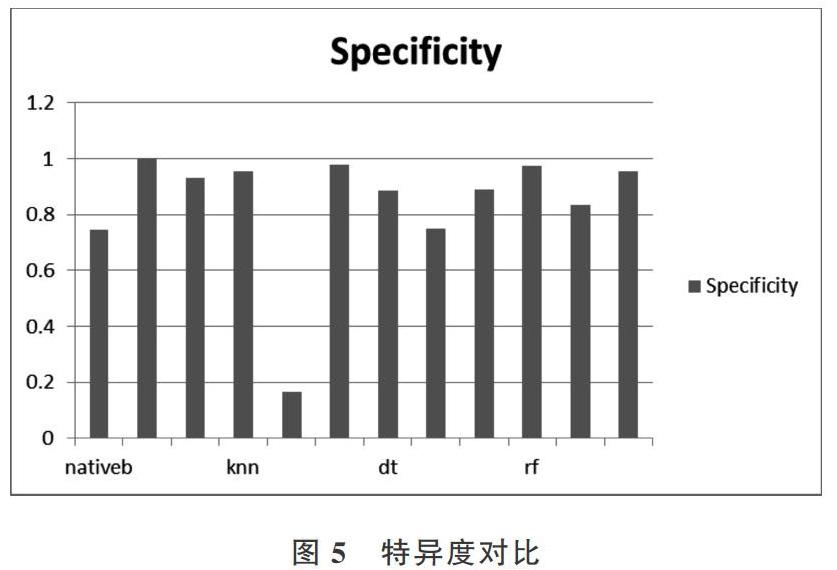
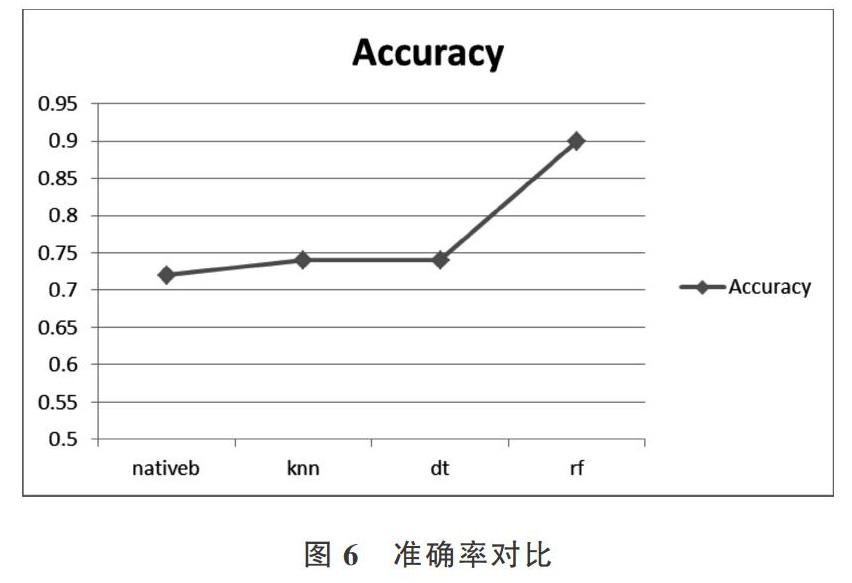
將樸素貝葉斯、KNN、決策樹和隨機森林分類算法的實驗結果召回率Sensitivity、特異度Secificity與準確率Accuracy進行對比，結果如圖4-圖6所示。

由上圖可以看出，隨機森林的召回率和特異度優于其它3種分類算法，且分類準確率明顯高于其它3種分類算法，故驗證了本文方法的正確性及有效性。

4 結語

本文將隨機森林分類方法應用于高考數學試題客觀難易度分類，大幅提高了分類準確率，為試題個性化推薦與自由組卷系統奠定了基礎。但由于網上開源的教育數據較少，故應用的實驗數據集較小，使用大數據集應能進一步提高分類準確率，但有待后續進一步驗證。另外，本文只分析了影響數學學科試題難易度的因素，對于英語、語文、生物等學科試題，其難易度影響因素還有待進一步分析與探索，這也將是未來的研究方向。

參考文獻：

[1] ALASTAIR P， CAROLYN M， et al. Language， contextual and cultural constraints on examination performance[C]. Jerusalem：the International Association for Educational Assessment，2000.

[2] HANNAH F H， SARAH H. What makes mathematics exam questions difficult[R].? Research and Evaluation University of? Cambridge Local Examinations Syndicate，2006.

[3] AYESHA A，ALASTAIR P. Curriculum demands and question difficulty [C]. Slovenia：IAEA Conference，1999.

[4] CHENG L S. On varying the difficulty of test items[C].? Annual Conference of theInternational Association for Educational Assessment， Singapore， 2006.

[5] 任子朝. 高考數學命題研究[J]. 中學數學教學參考，1994（5）：1-4.

[6] 李紅松，田益祥. 試題難易程度的判斷及其集對分析測定方法研究[J]. 武漢科技大學學報：自然科學版，2002， 25（2）：216-217.

[7] 教育部考試中心. 2008年普通高等學校招生全國統一考試大綱：理科[M]. 北京：高等教育出版社，2008.

[8] 候飛飛. 基于C4.5決策樹的試題難易程度分類研究[D]. 新鄉：河南師范大學，2016.

[9] 陳薈慧，熊楊帆， 蔣滔滔，等. 基于在線測評系統的編程題目難度研究[J]. 現代計算機：專業版，2018（13）：28-32，36.

[10] 曹開奉，王偉群，劉芳. 我國高考理科試題難度影響因素的文獻分析[J]. 考試研究，2018 （3）： 40-46.

[11] LEWIS D D. Naive （Bayes） at forty： the independence assumption in information retrieval[C]. European Conference on Machine Learning，1998.

[12] TANG Q Y， ZHANG C X. Data Processing System （DPS） software with experimental design， statistical analysis and data mining developed for use in entomological research [J]. 中國昆蟲科學：英文版， 2013， 20（2）：254-260.

[13] ROMERO C， VENTURA S. Educational data mining： a survey from 1995 to 2005[J].? Expert Systems with Applications， 2007， 33（1）：135-146.

[14] SVETNIK V， LIAW A， TONG C， et al. Random forest： a classification and regression tool for compound classification and QSAR modeling[J].? Journal of Chemical Information & Computer Sciences， 2003， 43（6）：1947.

[15] 張琳，陳燕，李桃迎，等.? 決策樹分類算法研究[J]. 計算機工程， 2011，37（13）：66-67.

[16] 王奕森，夏樹濤. 集成學習之隨機森林算法綜述[J]. 信息通信技術，2018，12（1）：49-55.

[17] 曹正鳳. 隨機森林算法優化研究[D]. 北京：首都經濟貿易大學， 2014.

[18] UTGOFF P E. ID： an incremental ID3[M]. Massachusetts：University of Massachusetts，1987.

[19] QUINLAN J R. C4.5： programs for machine learning [M]. San Mateo：Morgan Kaufmann Publishers Inc，1992.

[20] DEATH G， FABRICIUS K E. Classification and regression trees：a powerful yet simple technique for ecological data analysis [J].? Ecology， 2000， 81（11）：3178-3192.

[21] 孔英會.? 基于混淆矩陣和集成學習的分類方法研究[J].? 計算機工程與科學， 2012， 34（6）：111-117.

[22] 沈學華，周志華，吳建鑫，等.? Boosting和Bagging綜述[J]. 計算機工程與應用，2000， 36（12）：31-32.

[23] HUBER P J， STRASSEN V. Minimax tests and the neyman-pearson lemma for capacities[J]. Annals of Statistics， 1973 （2）：251-263.

[24] 陳冠民， 張選群， 陳華. 多序列相關系數及其估計[J]. 數理醫藥學雜志， 1999， 12（2）：101-102.

[25] ZAR J H. Significance testing of the Spearman rank correlation coefficient[J]. Publications of the American Statistical Association， 1972，67（339）：578-580.

[26] 宋亞飛，王曉丹，雷蕾. 基于混淆矩陣的證據可靠性評估[J]. 系統工程與電子技術，2015，37（4）：974-978.

（責任編輯：黃 健）