變式教學 變出精彩

肖宇鵬

摘 要：在初一階段的學生已經學過一元一次方程的應用，根據實際題干條件來設出未知數，列出一元一次方程求解來解答問題，但有的實際問題所列出的方程不是一元一次方程，而是一元二次方程，這就是本節課所要研究的一元二次方程的應用——關于面積和體積方面的實際問題。班級學生整體學習氛圍較為濃厚，有著良好的學習習慣。

關鍵詞：變式教學;初中數學;一元二次方程

在本節課中，學生要經歷和體會以一元二次方程來解答生活中的問題，認識到一元二次方程的重要性，發展自身邏輯思維能力、分析和解決問題的能力。

一、 復習鞏固，引入話題

在前期的學習中，學生已經學過為一元二次方程鋪墊的知識，教師不妨引導他們先進行復習，再自然引入本節課話題，避免教學內容的突兀，使班級學生自然過渡到本節課之中。

師：我們已經學習了與一元二次方程相關知識（概念、定理和運算法則等），大家思考下它與一元一次方程之間有著怎樣的區別和聯系？

生：二者間都有一個未知數，一元一次方程未知數最高次數為1次，另外一個為2次，一元一次方程解只有1個，另外一個有2個解。

師：概念不同，解法不一樣，解的情況也有所不同，這就說明一元二次方程的解法較為復雜，在選擇解法過程中要注意方法。那么，它們之間又存在著怎樣的聯系呢？

生：一元二次方程均可以化為一元一次方程。

師：我們學習新知識要基于舊知識，那么，一元二次方程實際問題解題步驟是什么？

生：審題、根據題干材料來設未知數、列出等式方程、運用所學知識解方程、最后驗證答案是否符合要求。

師：其中，最關鍵的步驟是什么？

生：根據題干信息來尋找等量關系。

師：認真審題非常重要，那么，我們今天就來研究如何利用一元二次方程求解與面積和體積相關的問題。

【設計意圖】：知識復習和引入簡單明了，從一元一次方程以類比學習方法來總結得到一元二次方程解決問題的步驟，引導學生進入本節課學習主題。

二、 問題探究，變式訓練

問題一：一根長度為22cm的鐵絲。（1）假設王叔叔要把鐵絲做成一個面積為30cm2矩形，求取矩形的長與寬。（2）如果要把矩形面積設計為32cm2，是否可以完成上述要求？

教師引導學生分析題干信息中的已知量和未知量，找到已知量為矩形的面積和周長，未知量為矩形邊的長度。

學生閱讀題干信息，找到已知量和未知量，設矩形的邊長為xcm，另外一邊長為（11-x）cm，找到其中的相等關系，在練習本上列出方程，判定解是否存在。針對班級學生可能出現的問題，教師在練習時到臺下巡視、指導，師生共同完成試題。在完成問題基礎上，教師再布置一些變式試題，既能鞏固所學知識，又能發散數學思維。

變式問題一：要想建立一個面積為20cm2的長方形場地，如果一邊靠著長6m的墻，其余三條邊用長度為13m的圍欄圍成，那么，這個圍成的長方形場地邊分別為多少？

（學生獨立完成后，教師選擇具有小組代表到講臺進行講解。）

組1：假設長方形的寬度為xm，那么長度為（13-2x）m。

組2：假設與墻平行四邊形的長度為xm，那么它的寬度為13-x2m。

變式問題二：如圖2，假設其他條件不變，要在長方形長邊上開出一道1m的門，那么，圍成的長方形場地長和寬各位多少？

（學生獨立完成后，教師選擇具有代表性的小組代表進行回答。）

組1：設長方形的寬度為xm，那么長度為（13+1-2x）m，長方形面積為x（13+1-2x）=20。

組2：設長方形的寬度為xm，那么長度為（14-2x）m，長方形面積為x（14-2x）=20。

組3：設長方形的長度為xm，那么寬度為14-x2m，長方形面積為x14-x2=20。

歸納環節：

師：在解決問題過程中，大家回憶一元一次方程的解法，探討如何來類比應用，在學習中有何收獲。

生1：要認真閱讀題干信息，找到隱藏在其中的等量關系。

生2：一元二次方程的求解要比一元一次方程復雜，解出答案后要對解進行驗證，看是否符合題干要求。

生3：本題是與面積相關的試題，假設未知量時要與長度和寬度有關。

生4：對未知量進行假設是本道試題解題的關鍵所在。

總結：閱讀題干—找到等量關系→做出假設—設未知量→進行求解—選擇恰當解法→注重檢驗→關注題干條件。

【設計意圖】：精心設計關于鐵絲圍長方形試題，以變式教學來注重培養學生數學方程思維，使他們能夠靈活應用思維來學習，在課堂中引導其進行數學思考，幫助個體掌握解決的方法。在試題練習的過程中，教師在教室中來回巡視，強調解答一元二次方程的注意事項，指導解題方法，使學生認識到一元二次方程重要性，借助一元一次方程的解法來提升他們的類比遷移能力，拓展其數學思維，達到高效率的課堂教學效果。

問題二：某塊長方形鐵皮，長度是寬度的兩倍，四個角各自截掉一塊正方形，制作出高度為5cm、容積為500cm3的無蓋長方體容器，那么，求這塊鐵皮的長度和寬度。出示試題后，學生用教具來演示長方體折疊過程。

學生對照教具，找到題干材料中隱藏的等量關系。

生1：長方體體積為500cm3，即，長乘寬乘高。

生2：長方形鐵皮長度是寬度的兩倍。

生3：設鐵皮的寬度為xcm，那么長度為2xcm，列出方程：5（x-10）（2x-10）=500。

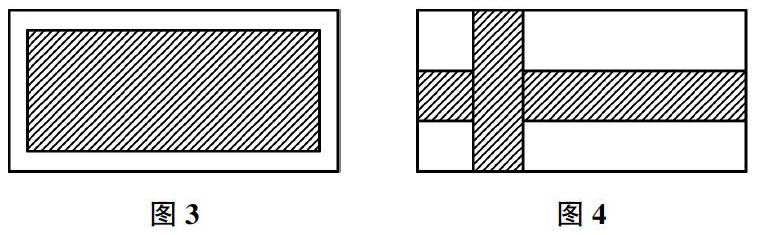
變式問題一：（1）如圖3所示，長方形草坪長度為30，寬度為15，在草坪的四周是等寬的路，如果包含路在內的長方形面積為544，那么，道路寬度為多少。

（2）已知包含等寬路在內的長方形草坪長度為30，寬度為15，其中，草坪的面積為364，那么，道路寬度為多少。

生1：假設道路寬度為x，根據題干信息得：（30+2x）（20+2x）=544。

生2：假設道路寬度為x，根據題干信息得：（30-2x）（20-2x）=544。

師：那么，根據上述知識，我們在生活中是否能得到以上述方程為模型的實際問題嗎？班級學生積極回應，踴躍回答問題。

生1：家里裝照片的相框。

生2：屋里的窗戶中間是玻璃，外面有等寬的密封條。

生3：桌面上的桌布。

師：大家回答非常棒，可否根據上述方程來編寫一道數學考題呢？

生4：為了讓講臺變得更美，我們用班費買了一塊講臺桌布，桌布的一邊和講臺等齊，另外三邊垂下等寬的寬度，求這個寬度為多少。班級學生紛紛根據題意來假設方程，列出方程式。

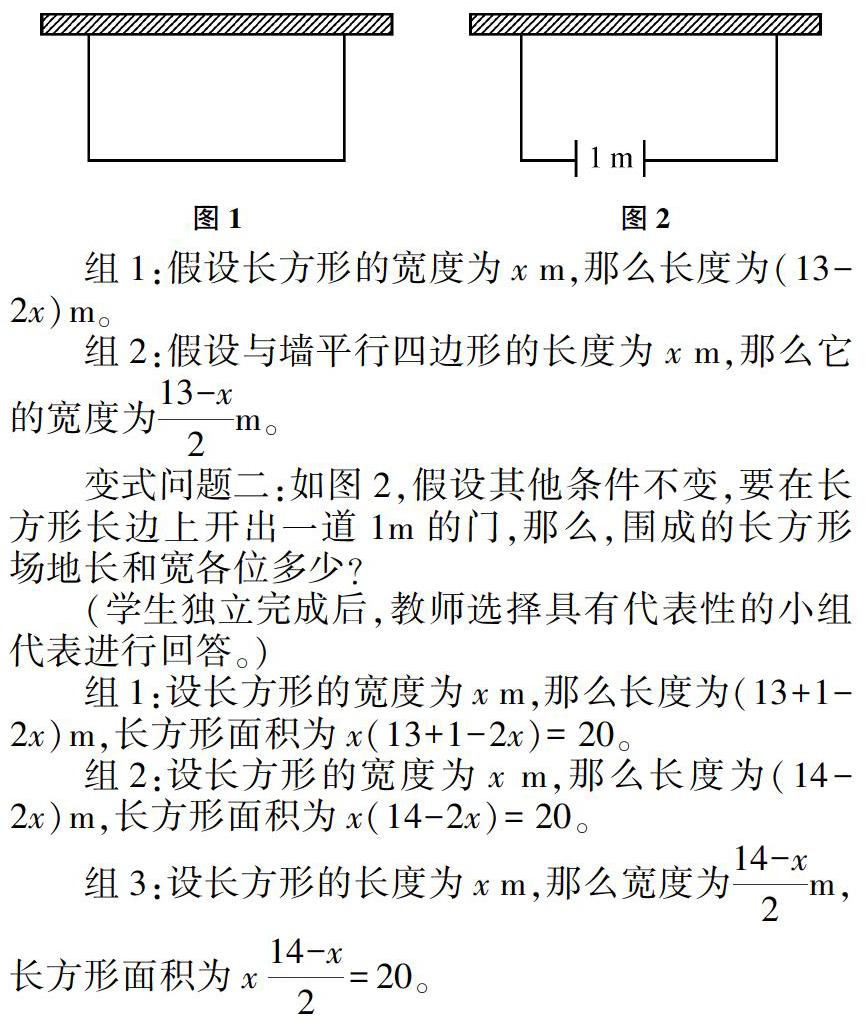
變式問題二：如圖4所示，在長度為40m、寬度為22m的矩形地面內，有兩條寬度相同且垂直的路，路之外鋪設草坪，要使草坪面積達到760m2，那么路的寬度為多少？學生根據題目來獨立完成，列出方程式。

師生共同總結用一元二次方程在解決面積和體積問題時的步驟、注意點，學會應用知識來解決與之相關的問題，從中體會到類比、轉化的數學思想。

【設計意圖】：根據長方形基本圖形進行改變，設計出其他圖形來進行變式教學，根據教學設計來與學生實際學情緊密結合，激發他們求知欲望，引導其把數學知識進行一般化思考，拓寬數學思維。小組合作引發個體對一元二次方程知識興趣，活躍課堂氛圍，引導學生當堂設計問題、當堂解答，加強對數學知識的理解和掌握，提升課堂學習質量和效率。

三、 教學反思

（一）明確變式目的

變式教學目的在于讓學生在問題的變化中找到內在的本質，發散數學思維，從“不變”的規律中來探索規律，從而更加透徹的理解問題背后的本質，學會用“不變”的知識來應對“變化”的題目。在問題發展的過程中，教師要幫助學生在理解基礎上來掌握如何解決問題，然后運用方法來解決數學問題，注重他們知識遷移能力的培養，拓寬個體的數學思維。

就本節課而言，教師展開變式教學目的在于運用一元二次方程來解決關于面積、容積的問題，在設計變式過程中通過改變題干信息、變換問題情境來創造出多種類型的變式，為學生練習創造更多機會，使他們從多個角度和層次對一元二次方程模型有更加深入理解，發散其數學思維，加強思維的變態。

（二）注重知識的生成

在實踐教學中，教師往往注重例題自身的變式，忽視了知識形成過程中的變式，課堂教學效果不夠理想。針對這一問題，教師不妨基于知識形成過程來思考如何對某個基本問題進行變式設計，引導班級學生運用數學思維來進行探究，使他們經歷知識的生成過程，體會到一元二次方程的數學本質。

本節課授課的重點是一元二次方程解決面積和體積問題，如果不精心設計數學問題，課堂訓練很容易變得機械、枯燥，試題講解也只注重重復性訓練。于是，從基本圖形入手設計具有一定梯度的變式試題，把問題變成“問題串”，層層遞進來推進數學課堂教學。

（三）提升課堂參與度

課堂教學效果在很大程度上取決于班級學生的課堂參與熱情，沒有了積極參與，哪怕再熱情，教學效率也會大打折扣。精心設計的變式能夠營造出一種寬松的課堂氛圍，使每個人都能掌握最基本的數學知識，培養他們的應變能力，開拓學習思路。數學教師設計問題來激發班級學生學習好奇心，使他們產生濃厚求知欲，提升課堂參與程度。在設計問題時，入口問題相對較為簡單，更容易被接受，借助于梯度問題來循序漸進展開教學，拓展數學思維，培養個體知識遷移能力。就本節課教學而言，設計的問題層層遞進且貼近學生生活，還讓他們現場編寫試題、現場解答，取得了良好數學課堂教學效果。

總之，教師在教學實踐中要注重變式的授課，依據教材和班級實際學情來合理安排講課內容，因材施教開展數學教學活動，為班級學生設計出一節精彩的變式課，有效提升個體數學學習興趣，使每個人都能樂在其中。

參考文獻：

[1]陳煥瓊.初中數學變式教學的過程性思考及案例研究[J].數學教學通訊，2017（12）.

[2]金榮.初中數學變式教學應用研究：以“探索勾股定理”的教學為例[D].呼和浩特：內蒙古師范大學，2017（11）.

[3]楊昌蘭.基于素養立意的初中數學課堂教學設計：以“垂直于弦的直徑”為例[J].中學數學教學參考，2017（10）.

[4]陳峰.“一題多解”是提高初中數學教學有效性的“催化劑”[J].中學數學研究：華南師范大學版，2017（9）.