借助工具，發展數學思考能力

吳軍強

【摘 要】 高中數學學習內容繁多，難度較大，為了進一步發展學生的思考能力與思辨能力，數學老師要嘗試借助相關的工具來推動數學課堂的開展。本文主要探討工具的選取、在課堂上的具體應用以及它的價值。

【關鍵詞】 高中數學;工具;思考能力

數學工具，顧名思義，是幫助學生思考的工具。其作為輔助材料，能夠幫助老師突破教學的重難點，完成本節教學的目標和任務。同時，利用工具開展數學活動時，老師可以有效地向學生滲透一些簡單的數學思想，培養學生的數學思維。

一、借助表格，豐富思維體驗

表格是一種最為常見的工具。制作表格，學生可以把零散的數據整體化，把復雜的問題簡單化。可以無形中向學生滲透“化繁為簡”“化零為整”的數學思想，讓學生獲得良好的思維體驗。

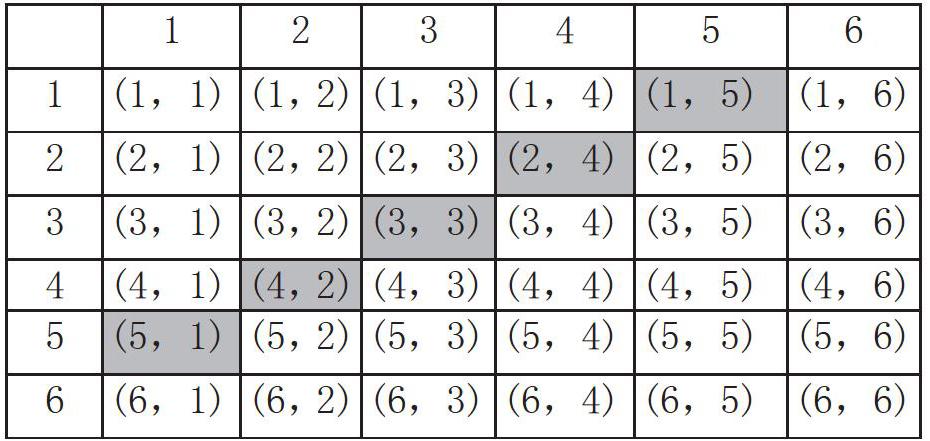
例如，在教學《古典概型》時，為了引出古典概型的概念，老師設置了一個與學生生活緊密聯系的數學問題：同時擲兩個骰子，一共有多少種不同的結果？其中向上的點數之和為6的結果有多少種？向上的點數之和為6的概率又是多少？投擲一枚骰子會出現6個點數，那么兩個骰子會有36種組合。有的同學嘗試用列舉法一一列舉，可是數據龐大，容易混淆，不太現實，而且數據零散，不容易看出其中的規律。綜合考慮，有的同學借助表格分析實際問題，列出的表格如下：

總共有36種情況，而向上的點數之和為6的結果總共有5種，已經在表格中標記出來。我們可以算出向上的點數之和為6的概率是。老師告訴學生：此概率事件屬于古典概型，并讓學生反思、總結提煉出古典概型的特點。學生已經了解基本事件的概念和特征，像這樣，表格中任何兩個基本事件都是相互獨立的，任何事件（除了不可能事件）都可以表示成基本事件的和。所以古典概型的兩個重要條件在于等可能性和有限性。每個事件發生的可能性都是相等的，基本事件的總數有限的，是可以表示出來的。同學利用表格對數據進行了整理，在整理數據中發現了古典概型的特點，有效地擴展了學生的數學思維。

二、借助多媒體，豐富操作體驗

幾何模塊也是高中數學的重要組成部分之一，幾何模塊的學習要求學生具有較強的想象力，能夠在腦海中想象出點或者是圖形的運動。因此，想象能力比較薄弱的學生可以利用多媒體，促進自己想象力的發展。

《幾何畫板》最突出的特點在于“動態變化”，它可以讓一個點隨意地運動，為學生的想象力提供了無限的可能。學生可以利用幾何畫板任意拖動圖形、觀察圖形，猜測并且驗證某個定理，在具體繪制圖形的過程中對圖形本身有著更為深刻的認識。在向學生普及《幾何畫板》這一思考工具時，老師可以先教學生一些基本的操作，帶領學生認識工具，學會編輯;然后讓學生繪制一些簡單的平面圖形，再上升到立體圖形;隨后可以從幾何模塊的學習過渡到函數模塊的學習。學生可以同時繪制指數函數、對數函數和冪函數的圖像，比較這三個函數圖像的特點，還可以便捷地畫出一些分段函數圖像。

例如，對“二分法求零點”這個定理的學習，很多學生認為這個定律比較煩瑣。對于在區間（a，b）上連續不斷，且f（a）f（b）<0的函數，通過不斷地把函數f（x）的零點所在區間一分為二，使區間的兩個端點逐步逼近零點，進而得到零點近似值的方法叫二分法。為了得到較為精確的零點近似值，學生首先要找準范圍，然后不斷逼近，計算多個準確的數值，過程十分煩瑣。但利用幾何畫板就可以省去計算的過程，在操作時對二分法定理進行驗證，進而深入理解定理，對學生數學學習很有幫助。與其讓學生花過多的時間在計算上，還不如讓學生動手操作體會二分法的實用性和價值。

因此，對于學生來說，幾何畫板是一個良好的學習工具，學生在課下可以探索相關的數學知識。對于老師來說，幾何畫板也是良好的教學工具，能夠把抽象的數學知識以簡單直觀的方式呈現在學生的眼前。

三、借助方格紙，拓展思維空間

方格紙是畫圖的材料，用方格紙畫出的圖形會更加規范和直觀。在方格紙上畫出圖形，分析圖形的特點，對比相關圖形之間的關系，能夠幫助學生理解一些數學概念。

例如，在教學《中心投影與平行投影》時，老師和學生一起先回顧三視圖的概念：光線從幾何體的前面向后面正投影得到的投影圖叫幾何體的正視圖，光線從左面向右面正投影得到幾何體的俯視圖，光線從幾何體的上面向下面正投影會得到俯視圖，這三幅圖統稱為幾何體的三視圖。老師向學生展示一個長為2厘米、寬為3厘米、高為4厘米的長方體，讓同學依次在方格紙上畫出它的正視圖、俯視圖和側視圖。方格紙和白紙有著較為明顯的不同：在白紙上畫圖，我們看不出長度關系，但是方格的數量可以表征出一定的數量關系。例如，將一個小方格的邊長設置為1厘米，兩個小方格就表示為2厘米。結合老師給出的長、寬、高等數據，同學依次畫出了這個長方體的三視圖。然后讓學生總結歸納三視圖的基本特征：一個幾何體的俯視圖和正視圖的高度一樣，俯視圖和正視圖的長度一樣，俯視圖與側視圖的寬度一樣，這也是本節課老師想要向學生重點傳授的三視圖口訣“長對正、高平齊、寬相等”。隨后老師又借助方格紙，讓學生分別了解中心投影、平行投影的概念和特點。學生學習完后便可以歸納出平行投影和中心投影的優缺點。比如，中心投影能夠逼真地反映物體原來的形狀，主要運用于繪畫領域。對于學生自我總結探索的規律和定理，學生會產生強烈的認同感，對學生的學習發揮了積極的作用。

高中數學知識點較為抽象，恰當地運用一些數學思考工具可以把抽象的知識直觀化，幫助學生理解和吸收。同時，利用工具進行學習可以做到深入思考，培養學生的思考能力。