數形結合法在高中數學教學中的應用研究

俞紅梅

摘 要數形結合是高中數學教學中一種十分常用的解題方法，通過在“數”與“形”間相互的轉化，使題目求解過程更為清晰，以提升解題效率。本文主要就“以數助形”與“以形助數”方面分別分析了對數形結合法的應用策略。

關鍵詞高中數學;數字;圖形

中圖分類號：A，G250.76，O711+.2 文獻標識碼：A 文章編號：1002-7661（2020）10-0101-01

隨著教育改革的深入推進，教育活動的開展更加關注對學生學習方法的傳授，重視其學科素養的形成與發展。而數形結合法作為高中數學中的一種重要解題方法，如何在教學實踐中實現對學生的有效滲透，以提升其解題效率，值得深思。

一、以數助形

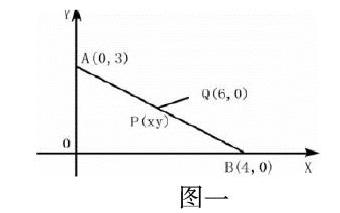
借助“數”實現對“形”的求解，是通過題目當中所提供的圖形，在經過觀察和分析之后，縷清其中所包含的數量關系，從而表達其相應本質屬性。在高中數學中，與以形助數相關的題目類型較多，對那些與學生已經掌握幾何性質有關的問題，便可通過適當轉化，使其成為對數量關系進行表達的形式，繼而利用代數運算和向量運算等多種方法，將題目化繁為簡，獲得更為簡便的解題方式，以優化學生形象思維的培養。在日常教學中，針對與幾何相關的數學知識，教師需要有意識地向學生逐步傳達“以數助形”思考方法，利用習題練習等手段，讓學生每當看到復雜圖形的時候，便可聯想到通過代數方法加以解答，從而提升解題效果。下面以坐標法為例，對“以數助形”方法進行分析。將幾何問題向坐標問題進行轉化，對幾何問題所具備的特征進行歸納，繼而構建與之相應的坐標系，從而實現向代數問題的過度，經過計算與推理，以獲得代數結論，最終將其重新代入坐標系，得到幾何結論。

二、以形助數

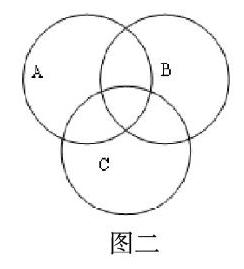
與“以數助形”相比，很多時候“以形助數”的難度跟大，對許多代數問題進行求解的過程中，不會像對幾何問題進行分析那樣很容易便想到數和形間的相互轉化，但在實際求解過程中如果沒有利用到圖形，非常可能造成解題過程十分繁瑣。接下來以集合關系問題為例，分析“以形助數”方法的應用。大家經常利用圓形代表集合，各個圓形之間相交的部分可以代表它們之間所存在的公共元素，而集合間相離便代表它們間并不具備公共元素。利用韋恩圖法，能夠十分直觀而高效地對集合關系問題加以求解。

例2：某公司一共有48名員工，公司開展趣味運動會，每人至少要參加一個項目，參加螃蟹接力跑（項目A）、托乒乓球賽跑（項目B）、袋鼠跳接力賽（項目C）的人數分別為28、25以及15人。其中，同時參與A項目和B項目的員工為8人，同時參與A項目與C項目的員工為6人，而同時參與B項目與C項目的員工為7人。求同時參與三個項目活動員工的人數。

解析：如圖二所示，三個圓形中的公共區域表示同時參與三個活動員工的人數。利用n代表集合元素，可以得到 ，因此28+25+15-8-6-7+ =48。解得 =1，所以同時參與三個活動員工的人數是1人。

三、結語

綜上所述，數形結合法是高中數學當中十分重要的一種解題方法，利用“數”與“形”間的合理轉化，以實現對解題流程的簡化效果。在日常教學中，教師要積極結合教學內容與學生的學習需求，有意識的向學生滲透數形結合法，通過教學方法的創新優化教學質量，以促進學生創新思維和解題能力的發展。

參考文獻：

[1]張繼連.解析高中數學數形結合解題技巧[J].數學學習與研究，2019（02）：106.

[2]鄧雅文.運用數形結合巧解高中數學解析幾何問題[J].科學技術創新，2018（03）：55-56.