崇尚智慧思考 提升思維品質

劉輝 陳凱平 李旭

摘 要：崇尚思考的課堂不是教師包辦的課堂，是學為主體的課堂;不是教為主體的課堂，是在研究中習得的課堂;不是被動接受的課堂，是主動探究的課堂;不是機械接受的課堂，是彰顯智慧與活力的課堂。崇尚思考的課堂，常借助幾何直觀，發展合情推理;常滲透數學思想，實現理性思考;常充分思辨探究，形成批判思維;常啟發多維思考，塑造靈動思維。

關鍵詞：崇尚思考;思維品質;理性思考

作為兒童生活的重要載體，課堂應是孩子自主的課堂，數學的課堂就是有效引導學生思維養成的課堂，注重培養學生的思維品質，即培養學生思維的邏輯性、思維的廣闊性、思維的深刻性、思維的獨立性、思維的靈活性、思維的敏捷性、思維的批判性等等……崇尚思考的課堂不是教師包辦的課堂，應是學為主體的課堂;不是教為主體的課堂，應是在研究中習得的課堂;不是被動接受的課堂，應是主動探究的課堂;不是機械接受的課堂，應是彰顯智慧與活力的課堂。

一、 借助幾何直觀，發展合情推理

《課程標準（2011年版）》指出：“推理是數學的基本思維方式，也是人們學習和生活中經常使用的思維方式。”學習數學就是要學習推理，尤其是史寧中教授把推理視為數學核心素養之一。具有一定的推理能力是培養學生數學素養和思維品質的重要內容，也是崇尚思考的數學課堂的重要目標。推理作為學習過程中重要的載體和素養，是抽象和隱性的，如果能借助幾何直觀，就能讓分析推理活動更具直觀化和顯性化，讓分析推理的思維活動更加得心應手、如魚得水。有時，我們的教學需要不僅僅是學生枯燥無味的回答，還要通過學習成果的直觀對比分析，查找相同和不同。通過幾何直觀的對比，進而對所學的問題進行深入的分析推理，達到更高效的教學效果。因此，應該多提供直觀的幾何圖形，讓學生在對比中進行分析探討和合情推理，深入理解知識的本質，累積合情推理的活動經驗，遨游于數學知識的海洋中，撥弄著思維的浪潮。

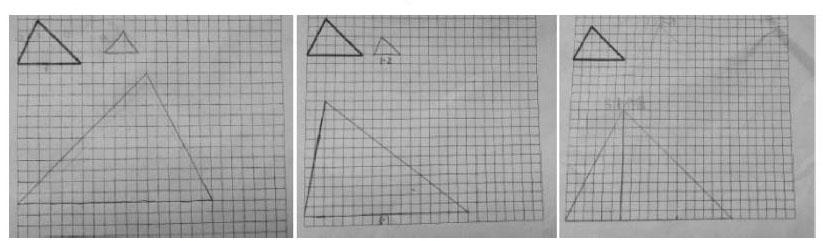
例如，六年級下《圖形的放大與縮小》一課，筆者在探究一般三角形分別按照1∶2和3∶1做縮小和放大圖形時，收集了三幅作品，先出示第一幅，問意見，生：“原來的圖左邊少一些，右邊多一些，而他放大和縮小之后不一樣了。”師肯定：“對，會類推對比，左邊要小點，右邊大點……（再一并出示第二幅）這樣行了吧？左邊小，右邊大！”生焦急地回答：“左邊太少，右邊太多了，變形了！”師：“是啊，放大和縮小要注意什么？”生1：“角度不能變。”生2：“圖形的形狀和結構不能改變。”師：“角度不變，那么要用量角器來畫？”生冷靜地說：“不用，只要看高的位置來定就好了。”師贊賞地說：“他提到了高的位置（出示第三幅），能具體說說嗎？”生：“原圖高的左邊是2格，按3∶1放大，高的左邊就要是6格。同樣，原來高的右邊是4格，放大后就要是12格。”師：“誰聽懂了？……這里的高左邊嚴謹點是指高的垂足的左邊，右邊呢？（垂足的右邊）這樣，咱們的高的位置就……（固定了）圖形還會變形嗎？會將圖形分段進行合情推理，并放大。這樣的策略值得我們學習。”

將學生的生成形象直觀、有層次地展示出來，讓孩子們經歷對比、分析和改進的過程，累積了對比合情推理的活動經驗，探究和感悟到數學的本質問題，既培養學生的空間想象能力和思考力，又提升了學生學會合情推理的思維品質。

二、 滲透數學思想，實現理性思考

數學思想是數學的靈魂。當一些代數問題復雜、抽象、難以理解時，我們都會借助數學思想來發現規律，進而解決問題，這就是數學思想的作用和優勢。數學思想有很多，例如，分類、轉化、數形結合等，這些數學思想都是一種解決問題的策略，讓學生的思考和問題的解決更具理性化和合理化。例如，當課堂上，遇到復雜的或大數據的問題時，運用化繁為簡的數學思想，就能幫助學生們從簡單的數據或問題入手，從基礎開始探究，通過探究慢慢深入數學的本質，找到數學規律后建構數學的模型，進而運用建構的數學模型表達世界，解決復雜或大數據的數學問題。而在經歷了化繁為簡的思維過程中，學生就能在觀察、對比、分析、聯系、推理的活動過程中，累積豐富的活動經驗，數學本質的探究和深度學習打下堅實的基礎。

例如，五年級上《植樹問題》一課，我校朱老師在出示例題之后，讓學生自主嘗試畫出要種多少棵樹，放手讓學生自主探究體會較大數據下的問題探究的復雜性和繁縟性。學生紛紛反映這樣的數據太難探究，即使找出來也很容易出錯，應該根據規律或公式來解決，這樣既省事又省力。根據學生自主提出的思想方法，朱老師引導學生化繁為簡：“既然350米很麻煩，那么大家覺得我們把路改為多少米會比較簡單，方便探究呢？”這下，學生的創造性被激活，有的說10米，有的說20米……層出不窮，朱老師在保證孩子們創新力的同時，還在引導學生思考的合理性，問：“為什么大家都選擇總長度是5的倍數呢？”學生立刻反應過來，原來剛才化簡的選擇過程中，大家理性地選擇了間距的倍數作為路的總長，更符合題意。

朱老師的課堂讓學生親歷化繁為簡的過程，感受數學思想的魅力，同時在運用數學思想的同時，讓學生理性思考，提升數學思維能力，提升核心素養。

三、 充分思辨探究，形成批判思維

全科核心素養中的科學精神，其中一個方面就非常重視批判質疑。批判性思維是創新意識的催化劑，更是科學精神的潤滑劑，它是基于充分的理性和客觀事實而進行理論評估與客觀評價的能力與意愿，不為感性和無事實根據的傳聞所左右。具有批判性思維的學生，通常不會迷信權威，善于反思，能在思辨探究中發現常人忽略的漏洞，并能抵制毫無根據的想法。教師可以在教學過程中把握培養思維批判性的時機，常常為學生創設思辨探究的活動平臺，通過思辨的過程，學生不僅能發展對比分析、區別聯系、邏輯推理、分類討論等邏輯思維能力，而且助力學生思維批判性的形成，培養批判質疑的精神品質，進而提升科學嚴謹的理性思維能力和精神品質。

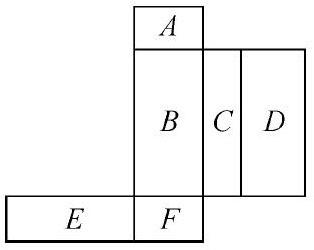
例如，五年級上《長方體的展開圖》有這樣一道題：下圖是一個長方體的展開圖，如果F在前面，從左面看是B，那么哪一面在上面？很多下想象能力很強的學生通過直接想象的辦法，直接喊出C的答案，緊接著學生通過動手實踐操作后能驗證了C面作為上面的結論的正確性。這位學霸由于在同學們心目中威望頗高，且自信十足，一下獲得了絕大部分同學的認同。就在大家都認為可以做下一道題時，有一個女生舉起了手，質疑到：“老師，我覺得還有可能E面是上面。”所有同學均對她投來了懷疑的眼光。這時，在對同學們的質疑的態度給予肯定與鼓勵同時，教師抓住這個契機，順水推舟，讓雙方展開了辯論與討論，還讓雙方都上臺親自折疊操作給大家看，通過實踐證明，所有同學均發現了一個事實：當F面上翻時，答案是E，當F面下翻時，答案是C，折疊的方向不同，結論也不相同。教師即使給予補充：“看來，很多問題我們多思考，多疑問，多反駁，我們會得到更多的收獲。”當思維撥開重重的迷霧，柳暗花明的剎那，學生思維得到了意想不到的升華，批判性思維的種子悄然間生長，壯大，而學生的學習力也在善于思辨中悄然成長。

四、 啟發多維思考，塑造靈動思維

思維的靈活性表現為機智、敏銳、富有獨創性。它決定于高級神經活動過程的靈活性，但這種靈活性不是固定不變的，而是能夠通過教育或自我教育的作用，得到發展或發生變化的。思維的靈活性常常會受限于思維定式的影響。如有的人在生活中總是反復使用一種固定不變的方式去處理問題，便會形成某種定型，阻礙思維的靈活性得到發揮。教師在教學過程中應當注重啟發學生多維度、多角度、全方位思考數學問題，讓問題解決的策略多樣化，引領學生的思維漫步于陽光大道，徜徉于曲徑通幽的小路，思維在潤物無聲之間越發靈動，富有活力。

例如，北師大版六年級上冊《探索規律》一節課中有這樣的一道題：將小棒一根一根像這樣擺成三角形，問擺100個三角形需要幾根小棒？學生通過化繁為簡，很快有學生列出了第一算式：1+2×100=201（根），教師追問道：“你是怎么想的？”生1回答道：“單獨先拿出一根小棒作為三角形的一邊，每增加一個三角形就增加了2根小棒，100個三角形就是100個2根，也就是1+2×100=201（根）。”師：“還有其他不同的方法嗎？”生2：“先擺第一個三角形的三根小棒，之后每增加一個三角形就增加了2根小棒，也就是3+2×100=201（根）。”受到兩個學生回答的啟發，其他學生不甘示弱，頓時思如泉涌。生3：“還可以單獨擺100個分開的三角形，再把它們兩兩拼在一起，一共重疊了99根，算式3×100-99=201（根）。”……師：“為什么擺同一個圖形，會有這么多種不同的算法呢？”生：“因為擺法不同，算法就不一樣，但是結果確是一樣的。”通過這樣的巧妙的教學設計，引導學生從不同角度，多維度進行思考，成功塑造了學生思維的靈動性。

綜上所述，崇尚智慧思考，提升思維品質，是數學尚思課堂的重要目標和要求。只有充分挖掘教學素材的內在價值，把握數學知識之間的本質聯系，引導學生用數學眼光去觀察、比較、思考、發現，滲透思想方法，才有可能在潛移默化間為學生思維發展注入新的驅動力，讓學生的思維品質發展更加理性、深刻。

作者簡介：

劉輝，福建省福州市，福州教育學院附屬第四小學;

陳凱平，李旭，福建省福州市，福州教育學院附屬第二小學。