數(shù)學(xué)建模思想在高中數(shù)學(xué)課堂教學(xué)中的應(yīng)用研究

吳靜怡

[摘? 要] 由于核心素養(yǎng)培養(yǎng)的是學(xué)生能夠適應(yīng)社會發(fā)展與終身發(fā)展的必備品格與關(guān)鍵能力，那么數(shù)學(xué)建模的教學(xué)也要重視學(xué)生品格的形成與能力的培養(yǎng)，又或者說應(yīng)當(dāng)通過數(shù)學(xué)建模的過程，實現(xiàn)必備品格與關(guān)鍵能力的培養(yǎng). 對數(shù)學(xué)建模思想在高中數(shù)學(xué)課堂教學(xué)中的應(yīng)用價值形成兩點認(rèn)識：認(rèn)識一：高中數(shù)學(xué)課堂教學(xué)中要重視數(shù)學(xué)建模的過程;認(rèn)識二：高中數(shù)學(xué)課堂教學(xué)中要重視數(shù)學(xué)建模思想的落地. 高中數(shù)學(xué)教學(xué)必須重視數(shù)學(xué)建模的價值，必須為學(xué)生提供數(shù)學(xué)建模的時間與空間，必須讓數(shù)學(xué)建模成為學(xué)生在數(shù)學(xué)學(xué)習(xí)過程中的重要指向.

[關(guān)鍵詞] 高中數(shù)學(xué);課堂教學(xué);數(shù)學(xué)建模思想;應(yīng)用研究

數(shù)學(xué)建模是數(shù)學(xué)學(xué)科核心素養(yǎng)的組成要素之一，數(shù)學(xué)建模在高中數(shù)學(xué)教學(xué)中的地位非常重要，是高中數(shù)學(xué)教學(xué)研究的熱點. 傳統(tǒng)的教學(xué)中，教師對數(shù)學(xué)建模的重視主要體現(xiàn)在建模本身，更多的是讓學(xué)生經(jīng)歷一個數(shù)學(xué)建模的過程，并在此過程中跟學(xué)生強調(diào)模型的重要性，以讓學(xué)生知其然且知其所以然. 應(yīng)當(dāng)說這一教學(xué)思路是比較先進(jìn)的，其超越了傳統(tǒng)的應(yīng)試認(rèn)識，更多的通過數(shù)學(xué)建模的過程指向?qū)W生學(xué)習(xí)能力的培養(yǎng). 那么在核心素養(yǎng)的背景之下，高中數(shù)學(xué)教學(xué)中的建模教學(xué)，應(yīng)當(dāng)有哪些相應(yīng)的變化呢？筆者以為這個問題值得探究. 由于核心素養(yǎng)培養(yǎng)的是學(xué)生能夠適應(yīng)社會發(fā)展與終身發(fā)展的必備品格與關(guān)鍵能力，那么數(shù)學(xué)建模的教學(xué)也要重視學(xué)生品格的形成與能力的培養(yǎng)，又或者說應(yīng)當(dāng)通過數(shù)學(xué)建模的過程，實現(xiàn)必備品格與關(guān)鍵能力的培養(yǎng). 基于這樣的認(rèn)識，本文從應(yīng)用價值、應(yīng)用實踐的角度進(jìn)行闡述，并做一概括.

數(shù)學(xué)建模思想在高中數(shù)學(xué)課堂教學(xué)中的應(yīng)用價值

通俗地講，數(shù)學(xué)建模就是在數(shù)學(xué)學(xué)習(xí)的過程中建立模型. 之所以要重視數(shù)學(xué)建模，是因為數(shù)學(xué)建模是聯(lián)系數(shù)學(xué)與現(xiàn)實世界的橋梁，是對現(xiàn)實問題的數(shù)學(xué)抽象，是綜合程度更高的素養(yǎng)，能夠高效地提升學(xué)生綜合實踐能力及自主獲取知識的能力，同時有利于學(xué)生其他數(shù)學(xué)核心素養(yǎng)目標(biāo)的達(dá)成. 因此，在高中數(shù)學(xué)課堂中應(yīng)用數(shù)學(xué)建模思想教學(xué)是非常必要的. 這種必要性首先體現(xiàn)在教師對建模思想的應(yīng)用價值的認(rèn)識. 筆者在實踐中不斷地積累認(rèn)識，然后進(jìn)行概括與梳理，對數(shù)學(xué)建模思想在高中數(shù)學(xué)課堂教學(xué)中的應(yīng)用價值形成如下幾點認(rèn)識.

認(rèn)識一：高中數(shù)學(xué)課堂教學(xué)中要重視數(shù)學(xué)建模的過程

對數(shù)學(xué)建模的教學(xué)有顯性和隱性兩種認(rèn)識，高中數(shù)學(xué)教學(xué)中應(yīng)當(dāng)將這兩種認(rèn)識進(jìn)行結(jié)合，根據(jù)筆者的實踐，有效的結(jié)合應(yīng)當(dāng)是：通過隱性的數(shù)學(xué)建模的過程，培養(yǎng)學(xué)生的數(shù)學(xué)建模能力;通過顯性的數(shù)學(xué)建模分析以及評價，培養(yǎng)學(xué)生對數(shù)學(xué)建模的認(rèn)同以及主動建模意識.

重視數(shù)學(xué)建模的過程就意味著在教學(xué)設(shè)計的時候，不僅要關(guān)注知識的形成過程，還要關(guān)注在知識形成過程中是否可以培養(yǎng)學(xué)生數(shù)學(xué)建模能力. 如果可以，又應(yīng)當(dāng)通過什么樣的途徑去培養(yǎng)學(xué)生的數(shù)學(xué)建模能力，換句話說，數(shù)學(xué)建模應(yīng)當(dāng)成為數(shù)學(xué)教學(xué)的一條主要線索. 只有對數(shù)學(xué)建模的過程給予了足夠的重視，教師才有了學(xué)生數(shù)學(xué)建模過程的研究動機，才能把握學(xué)生在數(shù)學(xué)建模過程中的認(rèn)知特點. 也只有把握了學(xué)生的認(rèn)知特點，才能經(jīng)歷一個真正有效的數(shù)學(xué)建模過程.

認(rèn)識二：高中數(shù)學(xué)課堂教學(xué)中要重視數(shù)學(xué)建模思想的落地

相對于數(shù)學(xué)建模的過程體驗而言，教師還應(yīng)當(dāng)引導(dǎo)學(xué)生在數(shù)學(xué)建模過程的體驗當(dāng)中領(lǐng)略思想. 數(shù)學(xué)建模思想并不是一個抽象的事物，在筆者看來，數(shù)學(xué)建模思想是指學(xué)生在數(shù)學(xué)建模的意識驅(qū)動之下，在面對實際問題的時候，能夠想到建立模型并通過建立的模型去分析或者解決問題. 這個觀點實際上也不是一個新鮮事物，有同行在研究過程中就有這樣的觀點：對于數(shù)學(xué)教學(xué)，其目標(biāo)應(yīng)當(dāng)定位到培養(yǎng)學(xué)生數(shù)學(xué)建模思想，以便學(xué)生在今后的學(xué)習(xí)工作當(dāng)中能夠運用數(shù)學(xué)建模思想解決實際問題. 簡單地說，學(xué)以致用就是數(shù)學(xué)建模思想的重要體現(xiàn).

數(shù)學(xué)建模思想在高中數(shù)學(xué)課堂教學(xué)中的應(yīng)用實踐

基于以上兩點認(rèn)識，在實際應(yīng)用的過程中，數(shù)學(xué)教師應(yīng)當(dāng)追求理論與實際的聯(lián)系，也就是說從理論上認(rèn)識到數(shù)學(xué)建模是運用數(shù)學(xué)思想、方法和知識解決實際問題的過程，它搭建了數(shù)學(xué)與外部世界聯(lián)系的橋梁，是數(shù)學(xué)應(yīng)用的重要形式，也是數(shù)學(xué)核心素養(yǎng)的重要組成部分;從實踐中認(rèn)識到，學(xué)生數(shù)學(xué)建模思想的領(lǐng)悟與素養(yǎng)的培養(yǎng)，是發(fā)生在具體的數(shù)學(xué)建模過程中的. 下面來看一個例子.

“函數(shù)”是高中數(shù)學(xué)知識體系中最重要的概念之一，同時也是最重要的數(shù)學(xué)模型之一. 傳統(tǒng)教學(xué)中往往只重視其知識定位，而忽視了其模型定位. 那么從數(shù)學(xué)建模的角度來看，函數(shù)這一概念的教學(xué)應(yīng)當(dāng)如何設(shè)計呢？對此筆者進(jìn)行了探究，現(xiàn)將數(shù)學(xué)建模視角下的函數(shù)教學(xué)設(shè)計與教學(xué)過程闡述如下：

第一步，創(chuàng)設(shè)情境. 生活中的與函數(shù)相關(guān)的問題還是非常豐富的，筆者選擇了學(xué)生相對熟悉的話費套餐作為素材，創(chuàng)設(shè)了這樣一個問題情境.

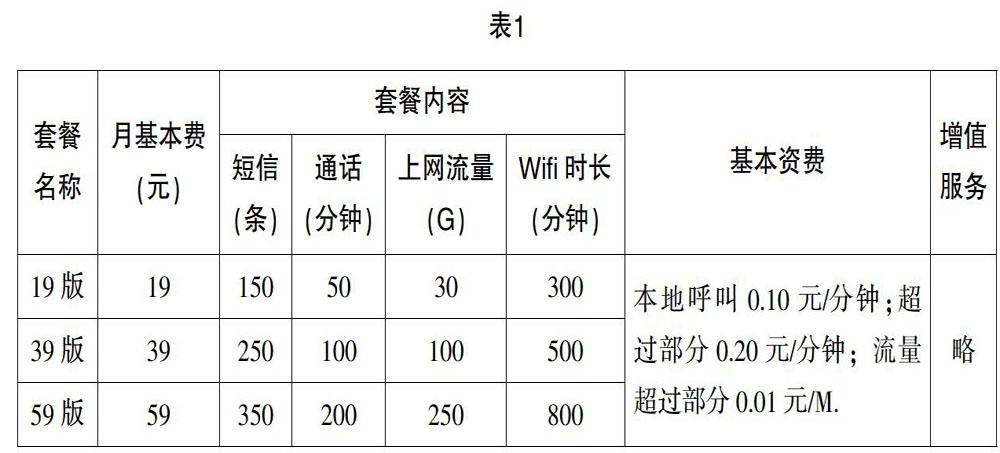
某通信公司推出了這樣一個話費套餐，具體包括四種類型，見表1.

面對這個套餐，應(yīng)當(dāng)怎樣選擇呢？這就是一個實際問題. 解決這個實際問題，可以根據(jù)經(jīng)驗，但是要想更為精確地做出判斷，就需要借助數(shù)學(xué)模型.

第二步，分析問題，并在此過程中形成數(shù)學(xué)模型.

事實證明，當(dāng)學(xué)生遇到這個問題時，他們的第一反應(yīng)也是根據(jù)經(jīng)驗去選擇，但是隨著討論的深入，他們發(fā)現(xiàn)數(shù)學(xué)在其中能夠發(fā)揮重要的作用. 比如有學(xué)生提出，在選擇套餐時，可以忽視短信與Wifi時長兩個因素，因為這兩者在實際生活當(dāng)中，很多時候都可以被忽視，既然如此，那就只要考慮通話與上網(wǎng)流量兩個要素，當(dāng)然同時也要考慮月基本費. 這個時候?qū)W生基本上都能夠從自身的需要出發(fā)，首先讓學(xué)生設(shè)身處地地思考——假設(shè)自己上了大學(xué)，然后估計自己一個月能支付多少錢，最后考慮自己的通信習(xí)慣與流量之間的關(guān)系. 在這樣的考慮過程中，模型就逐步呈現(xiàn)出來.

學(xué)生初步建立起來的模型實際上就是一個分段函數(shù)，以學(xué)生的分析為例：一個學(xué)生選39版套餐，原因是他判斷自己上網(wǎng)流量在100G左右，電話時間不會超過100分鐘，這個套餐是最合適的;而另一個學(xué)生則進(jìn)行了不同的判斷，他認(rèn)為自己每個月的通話時間與上網(wǎng)時間都不可控，因此選擇了59版套餐;最有意思的是那些精打細(xì)算的學(xué)生，他們首先對每一個套餐進(jìn)行了對比，用y=ax+by+cz來表示費用，其中a、b、c分別是短信、通話、流量的單價，而x、y、z分別是短信條數(shù)、通話時長、流量，然后去估算自己的使用情況，并代入這個函數(shù)，最后與基本費用進(jìn)行比較. 當(dāng)學(xué)生進(jìn)行到這一步時，實際上就已經(jīng)自發(fā)地建立了一個數(shù)學(xué)模型. 只不過這個數(shù)學(xué)模型是比較粗糙的，還需要教師引導(dǎo)學(xué)生進(jìn)一步分析，而這個過程與傳統(tǒng)的函數(shù)教學(xué)高度相關(guān)，在此不再贅述.

第三步，分析數(shù)學(xué)模型，反思建模過程.

從數(shù)學(xué)建模思想的領(lǐng)悟角度來看，由于上述建立數(shù)學(xué)模型的過程更多的是隱性的，因此必須引導(dǎo)學(xué)生進(jìn)行反思：自己是怎樣想到用函數(shù)表達(dá)式來解決問題的？這個思路在其他的哪些場合中還能運用？這一發(fā)現(xiàn)又說明了什么？在這些問題的思考與回答當(dāng)中，當(dāng)學(xué)生認(rèn)識到通過數(shù)學(xué)模型可以解決實際問題時，就可以認(rèn)為學(xué)生已經(jīng)初步形成了數(shù)學(xué)建模的思想.

數(shù)學(xué)建模思想在高中數(shù)學(xué)課堂教學(xué)中的應(yīng)用小結(jié)

核心素養(yǎng)對高中數(shù)學(xué)教學(xué)帶來的變化是明顯的，作為高中數(shù)學(xué)教師，要適應(yīng)并且積極面對這種變化，只要教師先適應(yīng)了這種變化，并且研究教學(xué)如何適應(yīng)這種變化，就可以讓數(shù)學(xué)建模思想在數(shù)學(xué)課堂上有效落地.

文章一開頭就已經(jīng)強調(diào)，核心素養(yǎng)強調(diào)關(guān)鍵能力的培養(yǎng)，其實數(shù)學(xué)建模就是一種關(guān)鍵能力，同時作為一個數(shù)學(xué)學(xué)習(xí)過程，在高中數(shù)學(xué)教學(xué)中，數(shù)學(xué)建模又是培養(yǎng)學(xué)生探究性學(xué)習(xí)能力的一個重要途徑. 重視數(shù)學(xué)建模的價值，讓學(xué)生經(jīng)歷一個充分的數(shù)學(xué)建模過程，并在數(shù)學(xué)建模過程中通過有效的反思，知曉自己是如何進(jìn)行問題的猜想與模型的假設(shè)的，是如何判斷模型的正確與否的，對于高中學(xué)生而言，通過這樣的反思，尤其能夠提高自己對數(shù)學(xué)建模的認(rèn)識. 這種認(rèn)識直接能夠支撐關(guān)鍵能力的形成.

總而言之，高中數(shù)學(xué)教學(xué)必須重視數(shù)學(xué)建模的價值，必須為學(xué)生提供數(shù)學(xué)建模的時間與空間，必須讓數(shù)學(xué)建模成為學(xué)生在數(shù)學(xué)學(xué)習(xí)過程中的重要指向. 只要做到這些，數(shù)學(xué)建模就一定能夠支撐起學(xué)生關(guān)鍵能力的養(yǎng)成，并有可能在此過程中幫助學(xué)生形成必備的品格.