巧用轉化策略提升解題能力

楊昆

摘要：小學數學涉及很多圖形知識，其中求解圖形面積、線段長度是重要考點。部分問題具有一定難度，不僅需要學生牢固掌握基礎知識，而且需要具備靈活的思維，需要根據給出的已知條件進行巧妙的轉化。為讓學生掌握轉化技巧，提升圖形問題的解題能力，教學中應做好題型的總結，為學生逐一的剖析，為他們解答相關習題帶來啟發。

關鍵詞：小學數學 圖形問題 解題能力

小學數學中涉及的圖形有三角形、平行四邊形、梯形、圓形以及長方體、正方體、圓柱體、圓錐體等，相關題型復雜多變，學生僅僅掌握基礎知識是不夠的，還應注重學習相關的解題方法與技巧，充分挖掘題干中的隱含條件并進行巧妙的轉化，才能實現順利求解。因此，教學中，教師應結合具體例題，為學生講解轉化的相關技巧，促進其解題水平的提升。

一、用割補法解答圖形問題

割補法是解決圖形問題的重要方法之一，具有較強的靈活性，需要根據已知條件對分開的、看似無規則的圖形進行割補，將之轉化為規則的、易于求解的圖形。教學中，教師應為學生講解割補法的相關知識，加深其對該種方法的認識與理解，提高其應用割補法解答圖形問題的意識。同時，為讓學生掌握割補法在解題中的應用，教師應篩選具有代表性例題，與學生一起分析解題思路，使學生在加深印象的同時掌握割補法適宜解答的題型、積累割補法應用經驗，以便再遇到類似問題時能夠及時找到解題突破口，實現快速、高效解題。

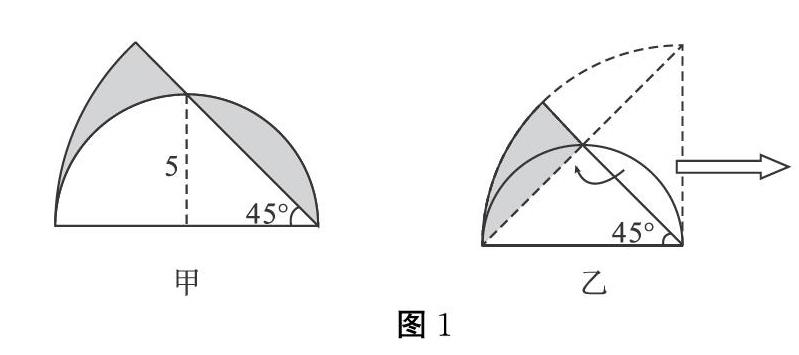
例1，已知半圓的半徑為5厘米，已知角度已在圖1（甲）中標出，求圖中陰影部分的面積（π取3.14）。

分析：圖1（甲）中的陰影部分是分開的，而且不規則，看似無法直接運用所學知識求解。事實上，可以將右側的陰影部分割補到左側與之對應的位置，然后運用扇形及三角形面積計算公式，通過作差求解。

解答：運用割補法將圖1（甲）轉化為圖1（乙）。由于半圓的半徑為5厘米，因此直徑為10厘米，對應扇形的半徑也為10厘米。由圖中45°角可知，扇形的面積為半徑10厘米圓的1[]8，對應圓的面積S圓=10×10×π=100π平方厘米，對應扇形的面積為S扇=1[]8×100π=12.5π平方厘米，而空白三角形的面積S三角形=1[]2×10×5=25平方厘米。綜上可知，陰影部分的面積S陰影=12.5×3.14-25=14.25平方厘米。

二、用平移法解答圖形問題

平移法是通過平移一些圖形，將原本看似復雜的圖形轉化為規則圖形的一種解題方法。通過平移，能降低分析問題的難度，提高解題的成功率。教學中，為讓學生掌握平移法，一方面，教師應講解使用平移法解答的例題，幫助學生弄清平移的思路。另一方面，應鼓勵學生總結適宜平移法解題的題型，尤其對于被分隔成多個部分的圖形，可考慮使用平移法進行轉化、解題。另外，應鼓勵學生積極思考，總結使用平移法解題的技巧，即根據題目要求，平移圖形時可將圖形適當變形，如在保持圖形面積不變的基礎上可將平行四邊形變形為長方形，從而降低計算復雜度。

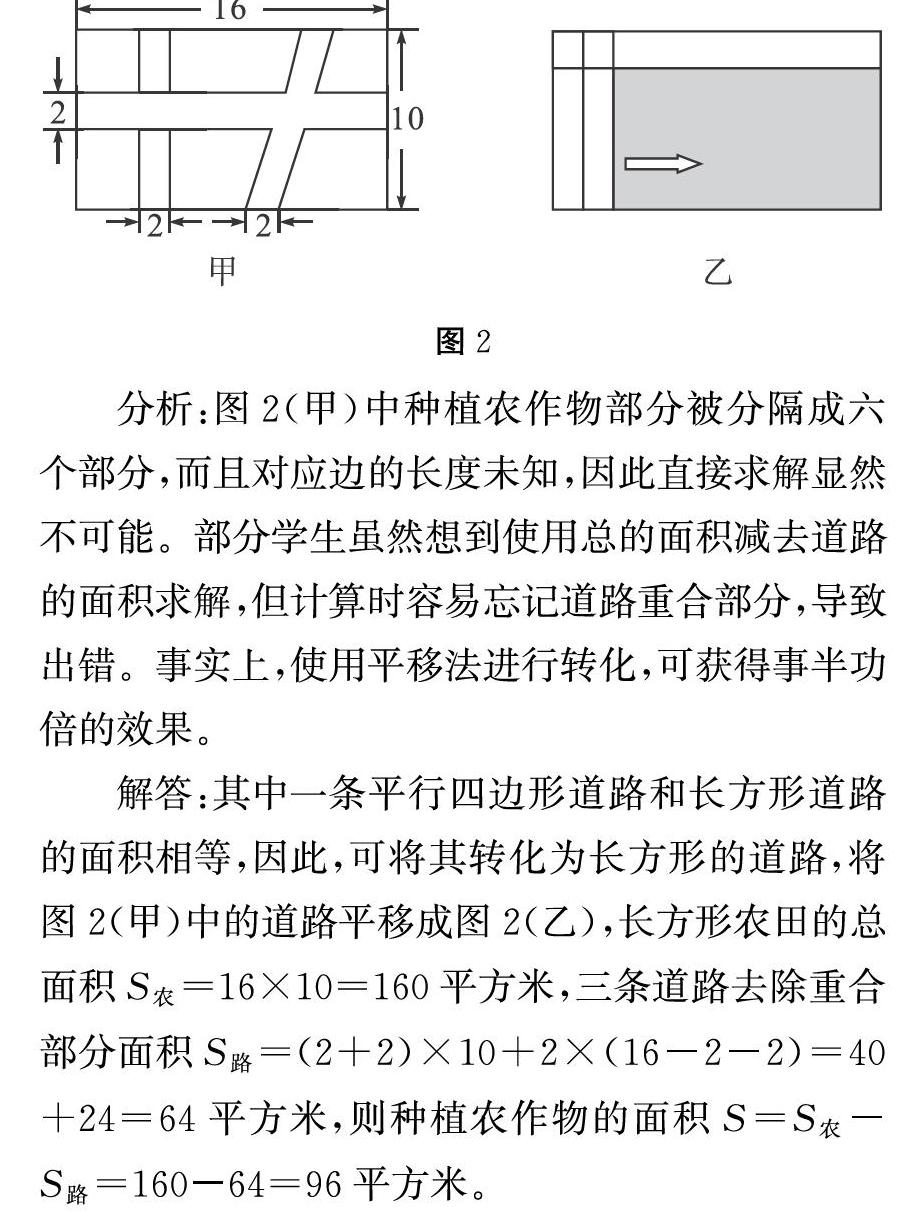
例2，如圖2（甲）為一塊長16米、寬10米的長方形農田，中間分布兩條長方形、一條平行四邊形的道路，道路的寬均為2米。則該農田種植農作物的面積有多大？

分析：圖2（甲）中種植農作物部分被分隔成六個部分，而且對應邊的長度未知，因此直接求解顯然不可能。部分學生雖然想到使用總的面積減去道路的面積求解，但計算時容易忘記道路重合部分，導致出錯。事實上，使用平移法進行轉化，可獲得事半功倍的效果。

解答：其中一條平行四邊形道路和長方形道路的面積相等，因此，可將其轉化為長方形的道路，將圖2（甲）中的道路平移成圖2（乙），長方形農田的總面積S農=16×10=160平方米，三條道路去除重合部分面積S路=（2+2）×10+2×（16-2-2）=40+24=64平方米，則種植農作物的面積S=S農-S路=160-64=96平方米。

三、用轉換法解答圖形問題

轉換法是一種間接求解圖形問題的方法。當采用直接法求解圖形問題的難度較大時，可轉換為求解問題的反面，得出反面的結果后，用總體減去反面，便可得出要求解的結果。為使學生熟練應用轉換法解答圖形問題，教學中，教師應展示相關例題，引導學生從整體上把握圖形，不要只盯著要求解的問題，通過轉換尋找解決問題的思路。另外，要讓學生多加練習，在訓練中積累轉換法的應用技巧，鼓勵學生多與同學溝通、交流，注重借鑒他人優點，不斷提升自己的解題水平。

例3，如圖3，長方形ABCD的長和寬分別為5厘米、3厘米，EF將其分成兩個長方形，在邊AB和CD上分布著大小不等的三角形，其頂點均落在EF上，求空白部分的面積。

分析：題目給出的已知條件非常少，對多數學生而言直接求解空白部分的面積難度較大。解題時可采用轉換法，通過求解陰影部分的面積間接的求出空白部分的面積。

解答：長方形ABCD的面積S長=5×3=15平方厘米。求解陰影部分面積時可先分析三角形面積的表達式，從中找到規律，而后進行解答。以長方形ABFE中的三角形為研究對象，其面積表達式均為1[]2×底×高。高均相等，等于BF的長，而各底加起來正好為AB的長，則其總面積為S1=1[]2×AB×BF。同理，在長方形EFCD中也存在這一規律，其總面積S2=1[]2×CD×FC，而AB=CD=5厘米，BF+FC=3厘米，則S1+S2=1[]2×AB×BC，表明其為長方形ABCD面積的一半，則空白部分的面積S=1[]2S長=7.5平方厘米。

四、用代換法解答圖形問題

代換法主要運用的是面積或線段相等，通過等量代換實現解題的一種方法，在解答小學數學圖形問題中應用率較高。為讓學生掌握這一重要方法，對題干進行巧妙的轉化，實現快速解題，教學中教師應引導學生關注圖形中的等量關系，如在長方形中兩條長和兩條寬分別相等、正方形中四條邊均相等。同時，設計針對性的問題，與學生一起分析、解答，使其深入理解代換法的具體應用。

例4，如圖4，ADHE為長方形，BCGF為正方形，其中正方形兩條邊和長方形AD、EH邊重合，其中FH=18厘米，AC=24厘米，求長方形ADHE的周長。

分析：題目中并未直接給出長方形ADHE的長和寬，需要從已知條件中找到等量關系，通過替換解答長方形ADHE的周長。

解答：由已知條件可知FH=18，AC=24厘米，即，FG+GH=18厘米，AB+BC=24厘米。則AC+FH=AB+BC+FG+GH=42厘米。又因為GH=CD，根據所學的長方形、正方形邊的等量關系可知，BC=FG=HD。則AC+FH=AB+BC+CD+HD，而AB+BC+CD=AD，因此，AC+FH=AD+HD，因此，長方形ADHE的周長=2×（AC+FH）=2×42=84厘米。

小學數學圖形問題教學中，為提高學生的解題能力，應讓學生認識到轉化的重要性，尤其要結合經典例題講解不同題型地轉化方法，包括割補、平移、轉換、代換等，讓學生掌握這些轉化方法的應用技巧以及注意事項，提高其靈活應用轉化思想解決問題的能力。

參考文獻：

[1]徐大蓮.小學數學高年級“圖形與幾何”錯題類型分析及對策研究[J].學周刊，2020（3）：20.

[2]葉品賢.基于數形結合思想的小學數學圖形與幾何教學研究[J].科學咨詢（教育科研），2019（9）：166.

[3]蔣敏杰.小學數學“圖形認識”教學的目標立意與實施策略[J].中小學教學研究，2019（2）：8-14.