厘清數學教學中的四個基本問題

【摘要】數學課堂教學是一個系統工程，影響教學效能的因素很多。課堂教學由教師的教、學生的學、教學內容三個基本部分組成。初中數學教學中，必須厘清“教（學）什么”“為什么要教（學）”“怎么教（學）、為什么這樣教（學）”“教（學）了之后有什么好處”等基本問題，這樣才能為一堂高效能好課提供保障。

【關鍵詞】新手課；教學反思；初中數學

【中圖分類號】G633.6【文獻標志碼】A【文章編號】1005-6009（2020）43-0027-04

【作者簡介】浦敘德，江蘇省無錫市新吳區教師發展中心（江蘇無錫，214027）科研評估部主任，正高級教師，江蘇省特級教師，江蘇省首批鄉村骨干教師培育站主持人，江蘇省基礎教育課改先進個人。

*本文系江蘇省中小學教研第十三期立項課題“基于數學核心素養的初中教材‘點·線·面解讀研究”（2019JK13-L041）的研究成果。

前階段，筆者擔任無錫市教育學會組織的青年教師賽課的評委，聽取了其中一組青年教師的課堂教學，本次賽課的課題是蘇科版數學八年級上冊“5.2平面直角坐標系（3）”。每位參賽教師都具有比較扎實的數學教學基本功，具體體現在課堂教學中目標定位合理、教學主線清晰、教學環節完整、教學語言簡潔、重點難點突出、板書設計合理等等方面。但每位教師在處理某些環節時，或多或少暴露出一些問題，體現了部分教師備課不足，對課堂教學的一些基本問題還沒有厘清，致使課堂教學中還是留下了不少遺憾。我們知道，數學課堂教學由教師的教、學生的學、教學內容三部分組成，他們互相融合構成一個有機的統一整體，只有根據教學內容把教師的教、學生的學都把握好，才能真正體現課堂教學效能的最大化。現把數學課堂教學中必須厘清的四個基本問題再次進行闡述，同時修正上述活動中參賽教師在課堂教學中暴露出的問題，希望廣大青年教師能從中獲得一些啟發和收獲。

一、厘清“教（學）什么”的問題

“教（學）什么”主要解決教學的內容問題。每課時要教學什么內容，對教師來說是一個比較容易認識到位的問題，但僅認識本課時教學內容是遠遠不夠的。因為數學知識內容是成體系的，具有整體性，從宏觀看是成面狀結構的；而每一章內容都是整體中的一個部分，具有關聯性，從中觀看是成線狀結構的；每一課時內容都是單元關聯知識鏈上的一環，具有獨立性，從微觀看是成點狀結構的。[1]基于上述對知識內容的認識，當我們思考其中一課時知識內容的時候，還應該搞清楚的是知識“點線面”結構，尤其是知識點的發展線。即本課內容是什么？找到“知識點”的位置，它從哪里來？將向哪里去？通過前后關聯，找到“知識線”所在。

從上可以看出，“教（學）什么”的問題伴隨而來的就是“課堂教學開始時溫故什么”和“如何進行前后知識關聯”的問題。就“平面直角坐標系”這節內容來說，共分三個課時，第一課時是直角平面坐標系概念的形成、通過坐標系這個工具進行點與坐標之間的數形相互轉換；第二課時是利用直角平面坐標系這個工具結合數學中最常見的平移、旋轉、翻折三種變換再次對點與坐標之間的相互轉換提高認識；第三課時是利用坐標系的工具屬性，建立適當的平面直角坐標系，用前面所學的知識解決生活與數學中的簡單問題。

可見，本課內容“建系”是前面兩課時知識的延續，也可以看成是前面知識的運用和應用。有了上面的知識內容認識，就可以解決部分教師賽課中暴露的第一個問題，那就是如何溫故？部分青年教師只知道把前面兩課的核心內容在課堂伊始進行回顧，卻不知溫故的目的在于知新。從上述知識發展線分析可以看出，只有服務于本課學習所需的學生數學現實（含知識、方法、經驗）與生活現實（含實際問題情境認識），才是最需要溫故的內容。還可以解決部分教師賽課中暴露的另一個問題，那就是拋開前面兩課時的知識、方法和經驗，把本課看作獨立的一課時，缺少前后課時知識之間的關聯。

二、厘清“為什么要教（學）”的問題

“為什么要教（學）”主要解決教學的必要性問題。蘇科版教材通常在每一課時的第一部分呈現的就是情境，情境必須具有有趣、有用、有挑戰性的特點。解讀情境時，如果給出的是數學情境，那就按照數學發展線提出數學問題，進而按照問題要求分析問題、解決問題；如果給出的是生活情境，可以先從生活情境中提出生活問題，再把生活問題變成數學問題，然后按照數學問題的解決思路展開教學。[2]不管是數學問題還是生活問題，最重要的一點就是在課堂教學中一定要讓學生充分體會到學習今天這個內容的必要性。

就本課時而言，教材素材一共提供了3塊內容，一是“電腦線路板機械手操作”問題，二是“旅游需要準確說出各景點的位置”問題，三是“正方形建立坐標系后求頂點坐標”問題。有的教師選擇“電腦線路板上機械手如何準確插孔”作為情境，有的教師選擇“游覽區如何準確說出各旅游景點位置”作為情境，這些選擇都沒有任何問題。部分參賽教師的問題就出在解讀生活情境時沒有讓學生充分體會到“建系的必要性”，或告知要“建系”或簡單問答后就“建系”，沒有充分體現出情境的價值。

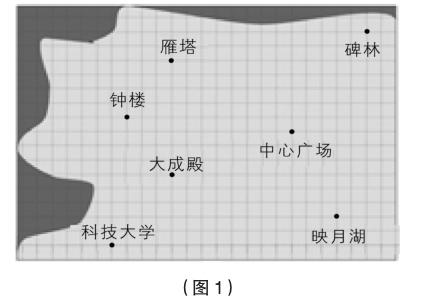
我們以“如果你站在中心廣場，你能根據這張旅游景點分布圖說清各景點的準確位置嗎？（見下頁圖1）”為例。要充分利用好這個情境，可以先讓學生說一說，如果在現實生活中，你會怎么做？由于學生已有了“5.1位置的確定”的知識、方法和經驗，學生肯定會提供各種各樣的辦法，教師需要指出這些方法存在的困難或局限，在此基礎上，進一步提問，在數學中，我們可以怎么做？由于學生有了“5.2平面直角坐標系（1）（2）”的知識、方法和經驗，學生必然會想到“建系”。只要建立了平面直角坐標系，那么就可以把每一個景點抽象成平面直角坐標系中的點，通過點的坐標就可以準確說出每一個景點的位置。接下去就可以研究如何建系的問題。