培養數學閱讀方式的教學實踐探討

韓榮

[摘? 要] 文章概述數學閱讀的特征，并結合案例探討閱讀的不同方式——領悟式數學閱讀、釋疑式數學閱讀、批判性數學閱讀，認為數學閱讀的作用是其他教學方式所無法代替的. 通過不同的數學閱讀方式，學生能形成數學概念，理解數學原理，進而掌握數學思想，形成數學素養.

[關鍵詞] 初中數學;數學閱讀;實踐

學生具備一定的數學知識與技能、經驗與觀念，是完成教學任務的必備條件，當這些條件不具備時，數學閱讀是最好的方式. 數學閱讀素養是生成學生其他素養的基礎，只有學生擁有了數學閱讀素養，其他素養才可以通過自身的努力逐步完善.

數學閱讀的特征

不同的學科語言決定了不同的學習方式，閱讀數學材料與閱讀文史類材料不同，由于數學知識具有結構的嚴謹性、語言的精確性及理論的邏輯性，所以，學生在進行數學閱讀時要講究精確，要做到有條理，才能有所收獲. 所以按順序逐字逐句地閱讀是數學閱讀的第一個特征.

要表述一個完整的數學知識，除了文字之外，還必須使用數學語言，即數學符號、幾何圖形、圖形表格等，這就需要學生理解每個數學語言的精確含義. 數學語言的精確性決定了文字語言不容許有含蓄、產生歧義的情況，所以學生只有弄清每一個數學符號、幾何圖形時，才能理解數學概念、數學原理或一個解答過程. 所以咬文嚼字是數學閱讀的第二個特征.

進行數學閱讀時，必須集中精力，心無他念，才能弄懂數學書面材料的順序、結構組成等. 如果學生對閱讀這部分材料沒有興趣，沒有意志力，那么就無法揭示數學材料中的數學思想，更不可能把數學思想轉化為自己的知識與能力. 同時，學生在認知上有錯誤的認識，抑或有數學概念或原理的缺失，那么在閱讀的過程中就會出現理解上的偏差，致使閱讀活動無法進行. 所以，全身心地投入是數學閱讀的第三個特征.

造成學生數學閱讀障礙的原因主要有兩個，一是以往學習數學知識上的欠缺或錯誤的認識;二是把數學中各個知識點孤立起來理解和認識，不能在腦海中形成知識結構體系，沒有認識到一些數學知識都是若干個數學對象彼此聯系、相互融合的結果. 所以數學知識的緊密聯系是數學閱讀的第四個特征.

數學閱讀的不同方式

方式就是說話、做事所采取的方法與形式. 做任何一件事情，要想取得成功，都要講究方式方法，數學閱讀也不例外. 要在數學閱讀中取得成效，就要講究數學閱讀的方式方法. 那如何培養學生良好的數學閱讀方式與方法呢？下面筆者與大家一起分享三種數學閱讀的方式.

1. 領悟式數學閱讀

進行數學閱讀時，如果產生一個數學問題，那這個問題的解決需要經過一個思維過程，它包括分析與綜合、演繹與歸納、抽象與概括. 雖然每個學生在每個環節所用的時間不盡相同，但這些環節都是必經的過程. 如果學生有一定的領悟能力，那對數學教材的理解只需要在感知活動中進行. 在感知活動中，可將新學習的內容與已有的概念、定理或解題思路進行對比，加工成個性化的內容. 領悟式數學閱讀最重要的是應有求異之心，其有助于從平常的現象中發現意想不到的新知識，具有化腐朽為神奇的力量. 當然，學生的領悟能力因個體的知識量、學習經驗不同而有所不同，進而會出現層次與水平的差異.

案例1？搖? “平面直角坐標系”教學片段.

師：你對坐標系這個概念有何認識？

生1：坐標系是為了確定平面內點的位置而創造出來的一種數學工具，與生活中電影院的座位、經緯網中的經度與緯度類似.

這是這位學生通過閱讀數學教科書后對“坐標系”形成的深層次領悟，說出了坐標系概念的本質.

師：如何用坐標系確定平面內點的位置呢？

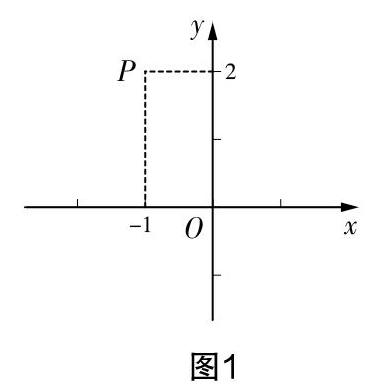
生2：過這個點分別作兩坐標軸的垂線，垂足在橫軸上的坐標就是它的橫坐標，垂足在縱軸上的坐標就是它的縱坐標. 如圖1所示，點P的坐標就是（-1，2）.

師：如何根據點的坐標在坐標平面內找出對應的點呢？

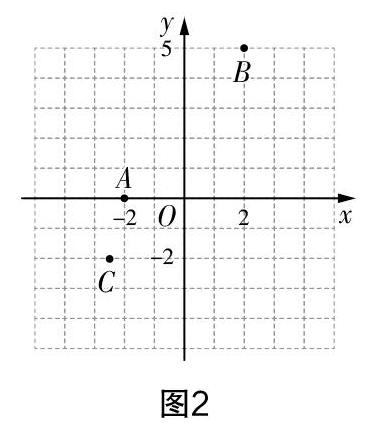
生3：在橫軸上找到橫坐標，過這個點作橫軸的垂線，在縱軸上找到縱坐標，過這個點作縱軸的垂線，兩條垂線的交點就是所要找的點. 如點A（-2，0），B（2，5），C（-2.5，-2）在平面直角坐標系中的位置如圖2所示.

領悟式數學閱讀對學生的要求比較高，學生要有創新精神，只有這樣，學生才能由教科書的表象過渡到數學的結構性本質. 需要注意的是，在創新的過程中，學生要克服消極的心理定式，要增強自信心，這樣才能居高臨下地掌握數學知識.

2. 釋疑式數學閱讀

學生進行數學閱讀時，可能由于經驗不足，或閱讀方法不對，不能深入到數學知識的本質結構，從而出現眉毛、胡子一把抓的情況. 如，忽略關鍵性詞語、數學概念之間的結構關系. 在這種情況下，教師要在關鍵地方精心設計問題，促進學生對數學本質的理解，培養他們的理性精神.

案例2? “一元二次方程根的判別式”教學片段.

師：根的判別式是如何判定一元二次方程根的情況的？

生1：當Δ=b2-4ac>0時，一元二次方程ax2+bx+c=0（a≠0）有兩個不相等的實數根;當Δ=b2-4ac=0時，一元二次方程ax2+bx+c=0（a≠0）有兩個相等的實數根;當Δ=b2-4ac<0時，一元二次方程ax2+bx+c=0（a≠0）沒有實數根.

師：能不能將判定中的“實數根”換成“根”呢？

生1：……可以吧……不可以吧……（學生一時之間難以回答）

師：判定中的“實數根”不能換成“根”. 這是因為，當Δ=b2-4ac<0時，一元二次方程ax2+bx+c=0（a≠0）仍然有根，只不過是虛根，而這種情況，同學們將在高中階段學到. 初中階段，數的范圍只限實數，當Δ=b2-4ac<0時，我們只能說這個一元二次方程沒有實數根，而不能說它沒有根.

師：當Δ=b2-4ac=0時，一元二次方程ax2+bx+c=0（a≠0）有兩個相等的實數根，此時可不可以說這個方程只有一個實數根？

生2：……可以吧……不可以吧……（學生一時之間又難以回答）

師：也是不可以的. 因為當一個一元二次方程只有一個實數根時，它可能還有一個虛數根，而當Δ=b2-4ac=0時，一元二次方程ax2+bx+c=0（a≠0）有兩個相等的實數根. 也就是說，任何一個一元二次方程都有兩個根，這兩個根可能是兩個實根，可能是兩個虛根，也可能是一個實根一個虛根.

在實際教學過程中，學生往往會對新學習的定理或法則只掌握一個大概，而不能深刻地把握與理解，其關鍵是不能找出定理或法則中的關鍵詞或核心詞. 此時，教師要把這些關鍵詞設計成問題，提出來讓學生思考與討論，以引起學生的重視和理解.

3. 批判性數學閱讀

在閱讀數學教材的過程中，學生應有質疑與批判的精神. 一方面，可以對教材所呈現的內容展開批判與質疑;另一方面，可以對自身的思維活動展開質疑與批判，即對運用知識經驗理解新知識的過程展開質疑與批判. 筆者在教學實踐中就有這樣一個很好的案例.

案例3？搖 “角平分線”教學片段.

角平分線的定義：如果一條射線把一個角分成兩個相等的角，那么這條射線就叫這個角的平分線. （大屏展示）

學生讀完以后……

師：同學們，這個定義對嗎？

生1：課本講的還有錯誤嗎？

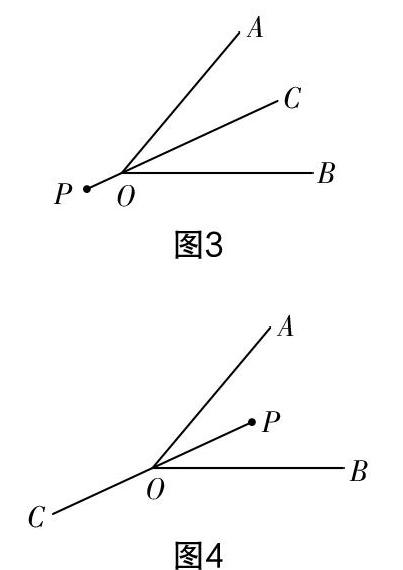
師：請繼續看下面兩個圖. （大屏展示）圖3、圖4所示的射線PC是∠AOB的平分線嗎？

生2：不是. 但這兩個圖形卻符合角平分線的定義，所以這里角平分線的定義是不夠嚴密的.

師：那大家討論一下應該如何定義.

同學們經過討論、批判、質疑……最終得到角平分線比較嚴格的定義，即“以角的頂點為端點的一條射線，在角內部把這個角分成兩個相等的角，這條射線叫這個角的平分線”.

閱讀教材時，我們一方面要做到不盲從，不迷信權威，要讓自己的閱讀與思維具有創造性;另一方面，要深入理解事物的本質，改造自己的學習經驗，不斷審視自己的思維過程，讓批判性閱讀發揮獨到的作用.

總結與反思

蘇聯斯托利亞爾認為，數學教學即數學語言的教學. 而語言的學習與閱讀相依相隨，數學閱讀包含感知和認讀、同化和順應、理解和記憶等心理活動，是一個不斷假設、證明、想象、推理的積極能動的認知過程. 教學中應重視數學閱讀，因為其獨特作用是其他教學方式所不能代替的. 學生在課堂教學中學習數學知識的時間是有限的，但預習、做作業、做試卷、做練習、網絡學習都離不開數學閱讀，所以只有通過數學閱讀，學生才能最終接收數學知識，形成數學概念，理解數學原理，進而掌握數學思想，形成數學素養.