核心素養背景下初中數學圖形微課教學探析

朱長青

[摘? 要] 核心素養背景下，微課的滲入，改變了過去固有的教學模式，其通過演示幾何動態，有效培養了學生直觀想象的核心素養;通過創設生活情境，有效培養了學生數學建模的核心素養;通過借助類比思想，有效培養了學生邏輯推理的核心素養.

[關鍵詞] 初中數學;核心素養;微課

核心素養背景下，微課的滲入，改變了過去固有的教學模式. 教學形式不再是一支粉筆、一塊黑板、一堂課. 傳統的數學課堂教學，學生只是一味地接受教育，課堂沒有生機與活力，教學效果可想而知. 微課致力于提高學生的參與程度，深刻剖析每一個知識點，運用現代教育技術手段達到了優化整合教學資源的目的，尤其在數學的圖形教學中更能發揮它的最大功效. 筆者以數學圖形教學為例，深刻剖析微課在培養學生核心素養過程中的作用，以供參考.

演示幾何動態，培養學生直觀想象的核心素養

核心素養是課程改革深化、素質教育落地的核心要素. 直觀想象是核心素養之一，也是有效課堂教學中一項重要指標，其包括直觀感知與空間想象兩種數學素養，要求學生能夠借助空間想象去感知幾何圖形的形狀、大小與相互位置關系等，達到對幾何圖形的理解，從而解決實際問題. 在日常課堂教學中，教師可以利用微課的演示功能，讓幾何圖形在視頻里動起來，讓學生通過直觀感受來探索數學問題的本質特征，在激發學生對數學學習的興趣，提高學生對數學知識的理解的同時，培養了學生直觀想象的核心素養.

例如，學生通過中位線定理，已經知道，連接任意四邊形四邊中點所得的四邊形是平行四邊形，那么連接矩形、菱形、正方形等特殊四邊形四邊中點所得的四邊形是什么樣的四邊形呢？對此，學生總是存在混淆. 再者，將這些命題反過來，即它們的逆命題正確嗎？學生一時語塞，如何讓中點四邊形的形象在學生心中留下深刻印象呢？筆者借助微課做了如下演示：

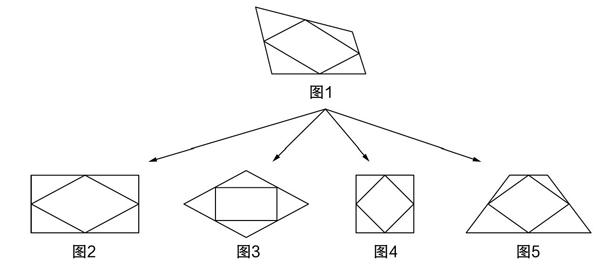
步驟一：在中點條件不變的情況下，讓四邊形分別變形為矩形、菱形、正方形、等腰梯形，看它們的中點四邊形是什么四邊形，如圖1、圖2、圖3、圖4、圖5所示.

通過這個演示，學生可以直觀地感知矩形的中點四邊形是菱形，菱形的中點四邊形是矩形，正方形的中點四邊形是正方形，等腰梯形的中點四邊形是菱形.

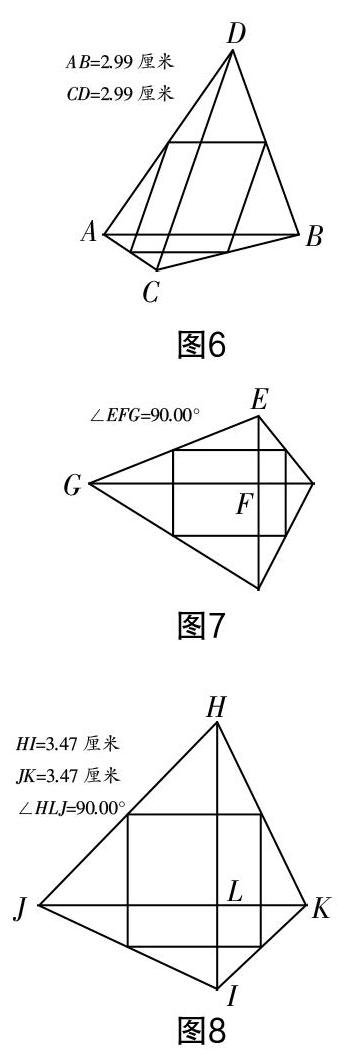
步驟二：那么將上述幾個命題反過來，它們的逆命題成立嗎？即中點四邊形是菱形的四邊形是否一定是矩形或等腰梯形呢？中點四邊形是矩形的四邊形是否一定是菱形呢？中點四邊形是正方形的四邊形是否一定是正方形呢？通過微課的演示，如圖6、圖7、圖8所示.

學生直觀地得到，中點四邊形是菱形的四邊形只需要滿足一個條件，即對角線相等;中點四邊形是矩形的四邊形只需要滿足一個條件，即對角線互相垂直;中點四邊形是正方形的四邊形只需要滿足兩個條件，即對角線互相垂直且相等.

整個教學過程，微課發揮了重要作用，它將圖形動起來，演示了在紙面上無法演示的無數種情況. 如讓一個四邊形的對角線相等，然后看它的中點四邊形是什么四邊形，在保證對角線相等的情況下，微課中的幾何畫板演示了無數種情況，以不可辯駁的事實，使學生認為只要對角線相等的四邊形，它的中點四邊形就是菱形，進而激發了學生的求知欲望，提高了學生課堂教學的參與度量，培養了學生直觀想象的核心素養.

創設生活情境，培養學生數學建模的核心素養

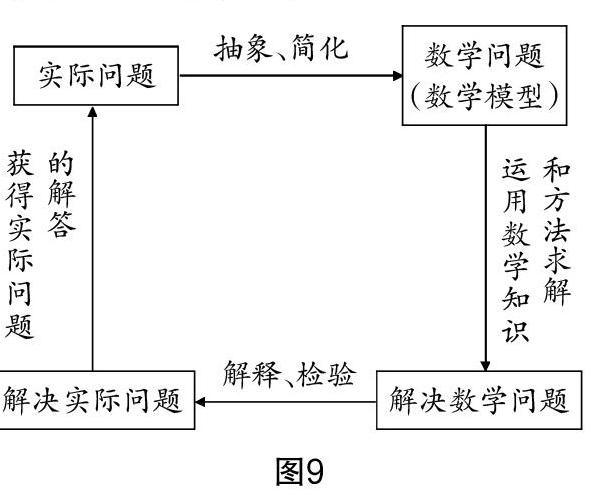
特級教師張思明提出，我們通過數學建模的教與學要為學生創設一個學數學、用數學的環境，為學生提供自主學習、自主探索、自主提出問題、自主解決問題的機會. 新課程標準中對數學建模的描述為，對實際生活問題進行抽象，把實際問題抽象為一個數學問題，然后用數學的語言、數學知識和方法進行構建，通過數學問題的解決從而解決實際問題的過程.它的流程圖如圖9所示. 可見，數學建模的過程可以培養學生應用數學的能力，培養學生的創造力. 在教學中，教師通過微課為學生創設一個學數學、用數學的生活情境，喚起學生的有意注意，吸引學生參與到課堂教學中，讓學生參與到發現、提出問題，探索、解決問題的全過程.

例如，在軸對稱與軸對稱圖形教學中，為了使學生對軸對稱有切實的生活體驗，微課視頻創設了這樣的生活情境：如圖10所示，它包括剪紙中的軸對稱圖案、蝴蝶、飛機、水中的倒影.通過生活情境的展示，學生感受到軸對稱圖形是指把這個圖形沿一條直線對折后，直線兩旁的部分能互相重合，建立了軸對稱的數學模型.

又如，在圖形的平移教學中，為了使學生對平移有切實的生活體驗，能從實際生活情境中抽象出平移這樣的數學概念，在微課視頻中設置了這樣的生活場景：如圖11所示，它包括電動平移門、徐徐上升的國旗、通過平移拼成的圖案、上升的電梯等.通過生活情境的展示，學生從中抽象出平移就是一個圖形的直線運動，它由移動的方向與距離決定，建立了平移的數學模型.

借助類比思想，培養學生邏輯推理的核心素養

在空間與幾何圖形的學習中，邏輯推理起著至關重要的作用，其是指從已知條件出發，應用定義、定理、公理推出一個命題是正確或錯誤的過程，包括歸納推理與演繹推理兩種形式，培養學生的邏輯推理素養，即是培養學生提出發現命題的能力，有理有據的說理能力，從而進一步理解數學知識之間的相互聯系. 教學中，教師可通過微課，借助類比的方法，培養學生的邏輯推理能力，提高學生獨立思考問題的水平.

例如，在學習圓內接四邊形的性質時，如何證明圓內接四邊形“對角互補”的性質呢？教學中，教師通過微課，先讓學生回憶圓周角定理的證明過程，微課中呈現了三種情況，即圓心在圓周角的邊上，在圓周角的內部，在圓周角的外部，如圖12所示.然后，教師讓學生類比圓心與圓周角的位置關系，猜測圓內接四邊形與圓心可能有哪些幾何關系，很快學生會畫出圓內接四邊形與圓心的三種位置關系，即圓心在圓內接四邊形的邊上、內部和外部，如圖13所示.類比圓周角定理的證明過程，學生通過作圓的半徑證明了三種圓內接四邊形對角互補.微視頻的呈現，勾起了學生的回憶，通過類比，發展了學生獨立思考的能力，提高了學生邏輯思維的縝密性與科學性.

微課作為一種全新的教學手段，培養了學生直觀想象、數學建模、邏輯推理的核心素養.實現了數學教學形式的多元化，廣大數學教育工作者，應善于反思勇于開發，相信微課的價值與作用會得到更多的開發與利用.