加強數學語言教學提升數學抽象素養
舒建明

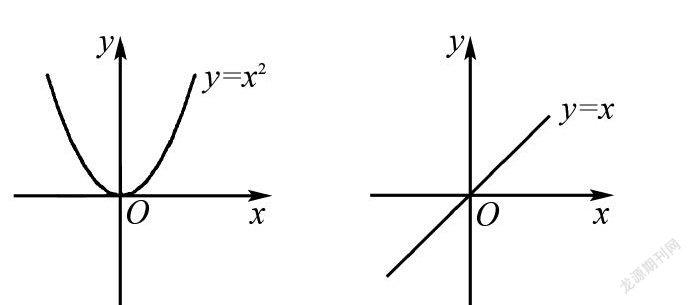
摘 要:數學抽象要求能從現實情景或數學情景中,概括出數學對象的一般特征,并用數學語言予以表征.因此,語言教學是數學教學的重要組成部分,提升學生的數學語言能力,是學生能夠進行數學表達、論證和交流的關鍵所在.教學中,教師不僅要創設情景,滲透三種語言的使用,也要在數學抽象過程中,規范對數學命題的表達和交流,并且在語言的不斷轉換表述中,將數學思維引向深入,從而深化對概念、命題和思想方法的認知.
關鍵詞:數學抽象;數學語言;語言轉換;數學思維
在《普通高中數學課程標準(2017年版)》指出,數學抽象是指通過對數量關系與空間形式的抽象,得到數學研究對象的素養.主要包括:從數量與數量關系,圖形與圖形關系中抽象出數學概念及概念之間的關系,從事物的具體背景中抽象出一般規律,并用數學語言加以表征.因此,能夠讀懂數學語言,學會用數學語言簡潔、準確地表述數學研究對象,并進行表達和交流,是數學抽象素養提升的重要顯性表現之一.
在新老教材的課程編排上,原來在2-2進行授課的內容“充分條件與必要條件”,“全稱量詞與存在量詞”,新教材也將其調整至必修一第一章開始學習.集合與常用邏輯用語是數學語言的重要組成部分,作為高中數學課程的預備知識,這一改變也凸顯了教材力求一開始即為學生用數學的語言表征世界打下良好的數學功底.
一、基于數學抽象素養下的數學語言發展的教學案例
數學語言在數學中的基本形式主要有三種,它們分別是圖形語言、文字語言、符號語言,下面以《函數的單調性》新授課為例,呈現數學語言滲透下的課堂教學案例.
1.教學目標
(1)用準確的數學語言歸納、抽象概括增函數和減函數的概念,并能正確理解單調性;
(2)利用圖象和定義判斷函數的單調性,能正確書寫單調區間,并能用單調性定義證明函數在給定區間上的單調性;
(3)培養學生抽象概括能力及數形結合思想方法的運用能力.
2.重難點
重點:(1)函數單調性的概念;(2)判斷和證明函數的單調性.
難點:理解函數單調性的概念.
3.教學過程
(1)創設情景
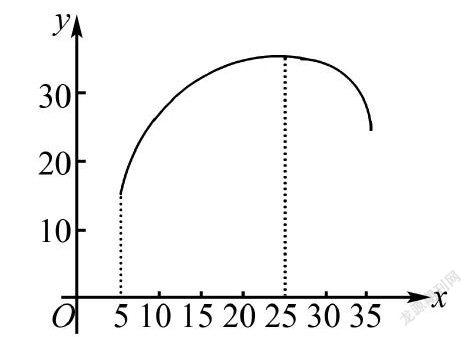
教師:前段時間,二師兄有點任性,身價一路飆升,豬肉價格飛漲.觀察右側豬肉價格走勢圖,說說該圖的圖形特點.
設計意圖:通過設計貼近生活的問題情景,初步感受兩個變量間的相互變化關系.同時也引導學生初步感受圖形語言對于描述實際問題的形象直觀,以及文字語言的通俗易懂.
(2)形成概念
教師:上面我們是從形的角度直觀感受了y隨x的變化情況,那我們是否可以從數的角度來研究這種y隨x的變化關系?我們從最簡單、最熟悉的函數f(x)=x2和f(x)=x圖象入手.
教師:如何描述函數f(x)=x2圖象在y軸右側的變化趨勢?
【設計意圖】通過具體的函數案例,結合圖形語言,引導學生嘗試用自己的語言即文字語言對函數圖象的變化情況作出描述,最后利用符號語言予以簡潔準確表征,從而將思維引向深入.
教師:你能仿照這樣的描述,用文字語言和符號語言說明函數f(x)=x2在區間(-SymboleB@,0]上是減函數和函數f(x)=x在R上是增函數嗎?
【設計意圖】學生通過模仿嘗試三種語言間的相互轉換,進一步深化對單調性的理解和熟悉,從而自然地從具體函數中抽象出一般函數的單調性概念.
(3)應用概念
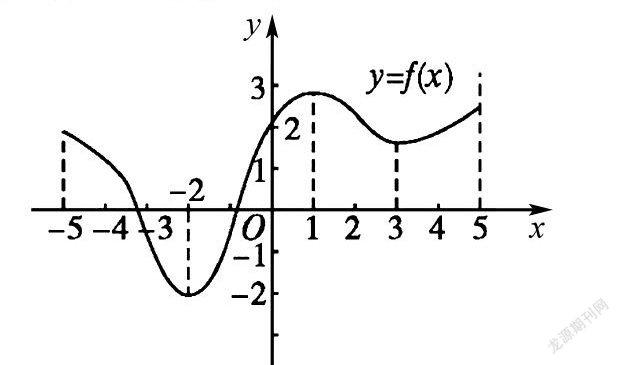
例1 如圖是定義在區間[-5,5]上的函數y=f(x),根據圖象說出函數的單調區間,以及在每一單調區間上,它是增函數還是減函數.
【設計意圖】通過有針對性的訓練,幫助學生能讀懂圖形語言并進行單調性的判斷
【例2】 物理學中的玻意耳定律p=kV(k為正常數)告訴我們,對于一定量的氣體,當其體積V減少時,壓強p將增大.試用函數的單調性證明之.
教師引導,板書展示,規范語言書寫.
【設計意圖】讀懂文字語言,并認識到其本質是研究數學單調性問題,從定義角度利用符號語言準確進行單調性證明,并明確用定義證明單調性的步驟
(4)辨析概念
探究:“函數f(x)=1x在定義域(-SymboleB@,0)∪(0,+SymboleB@)上是減函數”這個說法正確嗎?并說明理由.
學生:舉反例,取x1=-1,x2=2,f(-1)=-1<f(2)=12,所以在(-SymboleB@,0)∪(0,+SymboleB@)是減函數是錯誤的.
教師:你能寫出函數f(x)=1x的單調區間嗎?
學生:函數在(-SymboleB@,0)和(0,+SymboleB@)都是減函數
【設計意圖】:通過反比例函數單調性的研究,加深對定義中邏輯用語“任意”的理解,實現對概念的再認知.
二、數學語言對于數學抽象素養提升的意義
1.數學語言有助于數學概念和命題的恰當表征
恩格斯說:“一門學科只有當它用數學表示的時候,才能被最后稱為科學.”數學是研究數量關系和空間形式的一門科學.數學源于對現實世界的抽象,基于抽象結構,通過符號運算、形式推理、模型建構,理解和表達現實世界中事物的本質、關系和規律.數學語言作為表達科學思想的通用語言,具有準確、嚴密、簡明的特點.
概念抽象一般經歷兩個層次:第一層次抽象是直觀描述,有物理背景,用自然語言表達;第二層次抽象是符號表達,嚴謹、挑不出毛病.在教學過程中,教師通過情景創設,講具體背景,引導學生用自己的語言即自然語言初步建構數學問題模型,體會其中的數學思想和方法.自然語言具有通俗易懂的特點,可以實現對數學概念或模型的感性認識.為了更好的表征知識的內在結構特點,使數學的概念和命題更加簡潔,我們也可以對問題情景進行符號化表示,即進行第二層次的抽象.在語言的相互轉化過程中,我們不僅保證了知識形成的過程性,提高了語言表示的抽象層次,而且也實現了數學概念和命題的準確,恰當表征.
2.數學語言有助于數學抽象過程中思維的深刻性
數學抽象是指舍去事物的一切物理屬性,得到數學研究對象的思維過程.
數學語言是數學思維的載體,數學學習實質上是數學思維活動,在解決實際問題過程中,能否正確的在文字語言、符號語言以及圖形語言之間靈活轉換表征,是決定學生能否成功分析問題、解決問題的關鍵,這需要重視對數學語言能力的培養.在平時的教學中,我們應該注意對學生進行語言轉換的訓練,如數形結合、概念課教學等都是三種語言轉換的很好介質.
概念是數學思維的細胞,定理、公式等是數學思維的重要內容,表征是數學學習的中心,當學生在三種語言之間不同的轉換表征時,他們發展并加深了對數學概念的理解,數學語言的不斷轉換,能幫助學生交流他們的思維,并將思維引入深刻.
3.數學語言可以提升學生對問題情景的認知能力
眾所周知,浙江高考試題具有簡潔、樸實、明了的特點,但其背后卻是對學生數學語言閱讀、理解、轉化能力的高要求.數學語言在問題表達時雖然具有簡潔、準確的特點,但是符號較多、形式化程度高,這些都要求學生具有較高的數學語言認知能力.
學生只有將數學語言內化到自己的語言系統中,學生才能認讀感知問題情景中的有關數學術語和符號,并能正確依據數學原理分析它們之間的邏輯關系,最終實現對問題的本真理解,理清知識脈絡.
前蘇聯數學教育家斯托利亞爾說:“數學教學也就是數學語言的教學.”在教學中,教師只有不斷得創設問題情景,給予學生用數學語言表達問題的機會,提高數學語言的應用能力,確保學生在數學學習過程中“讀得懂,說得清,想得通”.
參考文獻:
[1]中華人民共和國教育部.普通高中數學課程標準(2017年版)[M].北京:人民教育出版社,2018.
[2]史寧中.數學的基本思想[J]. 數學通報,2011,50(1):1-9.
[責任編輯:李 璟]

