巧用數形結合,優化高中數學教學


摘 要:數形結合就是把抽象的數學語言、數量關系與直觀的幾何圖形、位置關系結合起來,通過以形助數或者以數解形來達到優化解題途徑或者學習過程的目的。數形結合的數學思想能夠讓學生對抽象的數字符號有更深的印象,能夠促使學生對直觀的幾何圖形有更深的理解。如果高中生能夠在三角函數圖象、性質、應用的學習中結合直觀圖形,那么學生就能收獲事半功倍的學習效果。因此,教師不妨巧用數形結合的數學思想,優化高中數學教學活動,從而全面提升教學質量。
關鍵詞:數形結合;高中數學;教學活動
數與形是數學中兩個最古老、最基本的元素,是數學大廈深處的兩塊基石。高中數學教師要將數形結合思想巧妙地運用到三角函數的教學中,從而揚數之長,取形之優,使得數形珠聯璧合、相映生輝,進而使得學生較為輕松地展開三角函數的學習探究。
一、引導學生運用數形結合的方式學習三角函數性質
三角函數的性質是三角函數的核心問題,學生只有熟練掌握了三角函數的性質,才能靈活運用其解決各種類型的問題。而三角函數的所有性質均能通過函數圖象表示出來,因此教師可以引導學生結合函數圖象來探索三角函數的性質。
如三角函數的對稱性,教師可以引導學生結合函數圖象來推導其對稱軸或對稱中心。以余弦函數為例,其頂點坐標可以是(0,1),可以是,還可以是……通過對函數圖象的觀察與分析,學生就可以總結出余弦函數的對稱軸。教師還可以引導學生運用數形結合的思想解決三角函數性質的相關問題,如函數的值域。學生需要先根據,求出,再結合正弦函數的圖象來解決問題,最終得到值域。
二、引導學生運用數形結合的方式展開三角函數的應用
三角函數作為描述現實世界中周期現象的一種數學模型,可以用來研究和解決很多問題。學生需要結合題目中的語言文字和其他信息建立函數解析式,然后做出相應的函數圖象,進而將實際問題抽象為與三角函數有關的簡單函數模型。可以說,運用三角函數解決數學問題的過程就是數與形結合的過程,就是數形結合思想運用的過程。
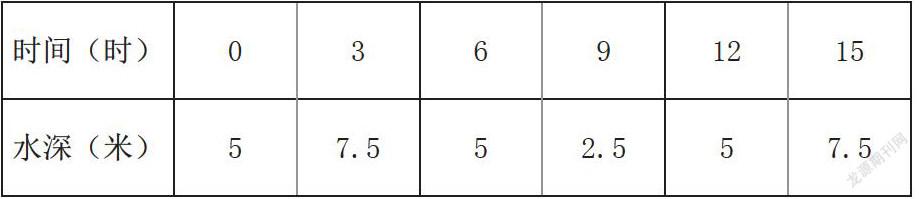
例如貨船進出港時間問題:一般而言,船在漲潮時駛進航道,靠近碼頭;卸貨后,在落潮時返回海洋。題目中會給出某一天具體時間與水深的一一對應的數據表格:
與該題目相關的問題有:選用一個函數來近似描述這個港口的水深與時間的函數關系;若一條貨船的吃水深度為4米,安全條例規定至少要有1.5米的安全間隙,該船何時能進入港口?在港口能呆多久?通過對數據的分析,學生就會發現,水深與時間的圖像有著周期性的關系,符合三角函數的相關特點,進而學生就可以建立三角函數的解析式。結合題意可知:貨船的安全水深為,也就是當水深大于5.5米時,貨船才可以進港,將5.5代入函數解析式中就可以求出相應的數值。
三、借助多媒體課件對學生展開數形轉化能力的培養
學生之間是存在個體差異性的,有學生看到某一函數圖象,其腦海中就能迅速想到與該圖象相關的性質特點;但是有學生看到某一函數解析式或者函數圖象后,其腦海中卻是一片空白,這就是學生之間的認知、思維差異。教育教學要尊重學生的個體差異,因此教師不妨運用現代化的信息技術制作多媒體課件,給學生創設個性化學習的平臺,從而讓每一個學生都能形成一定的數形轉化能力。
如,教師可以運用多媒體課件展開三角函數圖象、性質以及實際應用的總結與反思。課件中,教師可以分別呈現正弦函數、余弦函數以及正切函數的圖象、值域、對稱性、周期、單調性、奇偶性的相關知識。課件中,教師還要呈現三角函數實際應用的所有類型題目,有陽光照射方面的,有潮水方面,有溫度變化方面的等,只要是涉及到周期變化規律的,就都會運用到三角函數的相關知識。學生可以在課件的引導下,反復觀看函數圖象,從圖象中獲取相應的知識點,并總結運用三角函數解決實際問題的步驟策略,進而將數形結合的思想深深根植于腦海中。
總而言之,數形結合是數學科目中的重要思想,是學生走進數學大門所必需具備的知識技能。高中數學教師可以引導學生運用數形結合的思想來學習三角函數的概念、性質特點以及實際運用,從而促使學生在潛移默化中感受到數形結合思想的奧妙。
參考文獻
[1]淺談數形結合方法在高中數學教學中的應用[J].張曉亮.學周刊.2018(33)
[2]數形結合在高中數學教學中的應用[J].張莉蓉.課程教育研究.2018(37)
作者簡介:孫彥艷(1982.7—),女,漢族,籍貫:黑龍江,畢業于哈爾濱師范大學,現任教廣東省清遠市華僑中學,學士學位,專業:數學與應用數學

