一堂數學“母題”變式教學課的實錄與感悟

王敏

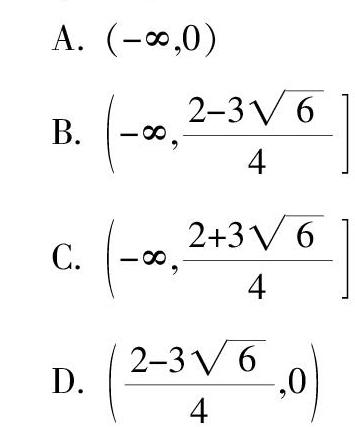
[摘? 要] 通過一堂導數與不等式的“母題”變式教學課的呈現，談幾點感悟，認為：“母題”變式教學體現了教師的主導作用和學生的主體地位，通過控制題量，有效實現了課堂教學減負，把學生的思維水平提高了一個層次.

[關鍵詞] 母題;變式;實錄;感悟

高考復習，從某個角度看，就是高考題型的研究和高考實戰演習. 如何研究題型，讓學生的實戰演習更有效. 筆者以為，“母題”變式研究與訓練，是一個不錯的選擇. 所謂“母題”變式，就是把一個典型例題作為“母題”，教師引導學生對其深入研究，并產生與之相關的系列題型，再讓學生訓練，這種從一道題引發數學研究的教學模式，不僅能讓學生“跳出題海”，更能讓學生感受自己編題（找題）自己做的樂趣[1]. 下文是筆者一堂導數與不等式的“母題”變式教學課的實錄與感悟，供大家參考.

教學實錄

1. 出示“母題”，引出復習課題

母題：（2018-2019學年湖北省黃岡中學、華師附中等八校聯考）已知函數h（x）=alnx+（a+1）x2+1（a<0），在函數h（x）圖像上任取兩點A，B，若直線AB的斜率的絕對值都不小于5，則實數a的取值范圍是（? ）

A. （-∞，0）

B. -∞，■

C. -∞，■

D. ■，0

教師提出問題：

問題1：這道題主要研究什么？

生1：利用導數研究不等式問題.

問題2：如何解這道題？即這道題的解題思路是什么？

生2：先對函數求導，將已知“直線AB的斜率的絕對值都不小于5”，去絕對值.然后構造函數f（x）=h（x）+5x，利用導數求得函數f（x）的單調區間，利用一元二次不等式恒成立問題的解法，求得a的取值范圍.

問題3：這道題主要考查什么？即考點是什么？

生3：本題考查利用導數的工具性研究不等式恒成立問題.

教師請學生根據剛才的分析自行完成，并展示. （這里略，答案：B）

教師出示本節課復習的主題：導數與不等式問題.

說明：教師對“母題”的選擇必須具有新穎性、代表性，且緊扣考綱與考點.

2. 集思廣益，總結子題題型

師：剛才的一道“母題”，體現了導數在不等式問題中的應用. 那么，利用導數能解決哪些不等式問題呢？請以小組為單位，加以探討，5分鐘后交流.

學生分組討論，教師巡視. 5分鐘后請以小組委派一名學生交流.

小組1：利用導數比較數值大小.

小組2：利用導數解不等式.

小組3：利用導數解決不等式恒成立問題.

小組4：利用導數證明不等式.

教師點評：同學們剛才集思廣益后提出的四種問題，的確是導數與不等式的最常見的四種題型. 在高考真題和各地的模擬卷中，這四類問題頻頻出現，主要考查考生對導數的靈活應用，我們不僅要把握基本題型，更要把握具體的解題方法.

？搖3. 分組組題，展示資料共享

師：有道是“是牛是馬，牽出來遛遛”. 空口無憑，有例才為證. 請同學們，繼續以小組為單位，找出與本組提出題型有關的題目2至3個.

教師繼續巡視，及時回答學生組題時遇到的問題或疑惑. 20分鐘后仍以小組為單位委派一名學生進行交流.

小組1：剛才我們小組歸納的題型是利用導數比較數值大小，請看下面的3個題：？搖？搖？搖？搖？搖？搖？搖？搖？搖？搖

（1）已知函數f（x）=■，則f（2），f（e），f（3）的大小關系是______.

（2）函數f（x）在定義域R內可導，若f（1+x）=f（3-x），且當x∈（-∞，2）時，（x-2）f′（x）<0，設a=f（0），b=f■，c=f（3），則a，b，c的大小關系是______.

（3）f（x）是定義在非零實數集上的函數，f′（x）為其導函數，且x>0時，xf′（x）-f（x）<0，記a=■，b=■，c=■，則a，b，c的大小關系是______.

？搖 小組2：剛才我們小組歸納的題型是利用導數解不等式，請看下面的3個題：

（1）已知函數f′（x）是函數f（x）的導函數，f（1）=■，對任意實數都有f（x）-f′（x）>0，則不等式f（x）

（2）定義域為R的可導函數y=f（x）的導函數為f′（x），滿足f（x）>f′（x），且f（0）=1，則不等式■<1的解集為________.

（3）定義在（0，+∞）上的函數f（x）滿足x2f′（x）+1>0，f（1）=6，則不等式f（lgx）< ■+5的解集為________.

小組3：剛才我們小組歸納的題型是導數與不等式恒成立問題，請看下面的3個題：

（1）已知函數f（x）=ax3-3x+1對x∈（0，1]總有f（x）≥0成立，則實數a的取值范圍是________.

（2）已知a，b∈R，直線y=ax+b+■與函數f（x）=tanx的圖像在x=-■處相切，設g（x）=ex+bx2+a，若在區間[1，2]上，不等式m≤g（x）≤m2-2恒成立，則實數m有________.

？搖（3）設函數f（x）在R上存在導函數f′（x），對任意的實數x都有f（x）=4x2-f（-x），當x∈（-∞，0）時，f′（x）+■<4x. 若f（m+1）≤f（-m）+3m+■，則實數m的取值范圍是________.

小組4：剛才我們小組歸納的題型是導數與不等式的證明，我們找到了下面兩道題，供同學們參考：

（1）已知x=1為函數g（x）=x（lnx-c）的極值點. 證明：當x>1時，g（x）

（2）已知函數f（x）=■-lnx. ①求f（x）的單調區間;②求證：ln■≤■.

4. 點撥思路，學生獨立完成

師：同學們組的題目都緊扣題型，十分精彩，我發現有些題目還是最新出現的模考題，這說明我們同學身邊的資料真的不少，開卷有益，它山之石，可以攻玉，這很好！同學們找題的目的是為了解題，那么這類問題該如何解答？利用導數解決不等式問題，歸根到底是利用導數研究函數的單調性，進而再利用函數的單調性解決問題[2]. 因此，解決這些問題，一般都要構造函數，本質上看，這類問題考查的還是導數與函數的關系.

師：好，今天的作業就是請大家完成剛才大家組的11個有關導數與不等式的題目，請注意：原則上獨立完成，若確有困難，則允許合作討論.

三點感悟

感悟1：數學習題課一般都是由教師提供題目，學生練習題目，學生只顧埋頭做題，往往不知題從何來，不知題目所涉及的考點，這樣的練習往往缺乏對題目的研究，是一種為解題而解題的復習模式，學生不能對題目產生理性的認識. 而從教師提供的“母題”出發，讓學生自己去找題，要完成這個任務，學生務必明確題型，否則很難“對號入座”，于是將學生的“解題”轉化為“題解”，從而把學生的思維水平提高了一個層次.

感悟2：減負，是當今中小學教育界沉重的話題. 如何將學生從沉重的課業中解放出來，讓他們“跳出題海”，是每位教師關心的問題[3]. 而“母題”變式教學模式，從很大程度上控制了題量，并允許合作完成，從而讓他們練有所獲，練有所成. 與此同時，也減輕了教師的負擔，讓學生自行找題，有時會更切合實際，比教師找題更有效. 自己選的題目自己做，這更能提高學生訓練的積極性.

感悟3：任何一堂課都應該體現教師的主導作用和學生的主體地位. 教師一講到底，這種“填鴨式”的教學模式完全削弱了學生的主體地位，早已被大家摒棄. 而“母題”變式教學模式，教師儼然是教學的組織者和指導者，而不是“主宰”，探討的問題雖然由教師引發，但問題的進展由學生決定，這種把學習的主動權交還給學生的教學模式，能使課堂氣氛和諧，師生關系融洽，從而能達到較好的教學效果.

參考文獻：

[1]? 江衛軍. 高中函數母題研究[D].蘇州大學，2016.

[2]? 趙子兵. 利用導數處理與不等式有關的問題[J]. 中學數學研究，2011（12）.

[3]? 范爽. 關于“課業負擔”的若干基本理論問題研究[D]. 沈陽師范大學，2013.