巧用幾何圖霸,優化數學教學
周小毛

【摘要】《幾何圖霸》是信息技術教學手段其中的一項教學工具。在數學的教學過程中,只有充分利用好信息技術來營造一種新型的教學環境,才能實現既能發揮教師主導、又能充分體現學生主體地位的教學方式,更好地達到培養學生獨立自主的學習能力、創新能力和實踐能力的目的。
【關鍵詞】數學教學 ? 信息技術 ? 幾何圖霸 ? 教學工具 ? 方法策略
為提高教學效率、優化課堂教學,我嘗試過多種教學軟件的運用,其中我認為最具可操作性和實用性的要數《幾何圖霸》了,具體表現如下:
1.借助《幾何圖霸》激發學生學習數學的興趣
數學難教,如何教好?盧梭告訴我們:“不在于教他各種學問,而在于培養他有愛好學問的興趣,而且在這種興趣充分增長起來的時候,教他以研究學問的方法”。為了搞好數學教學,我將《幾何圖霸》引入課堂,并利用其豐富的動態圖像和靈活多變的形式,來刺激學生對學問的好奇心和對數學知識的求知欲望。
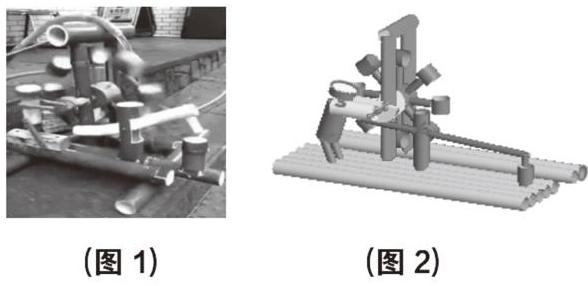
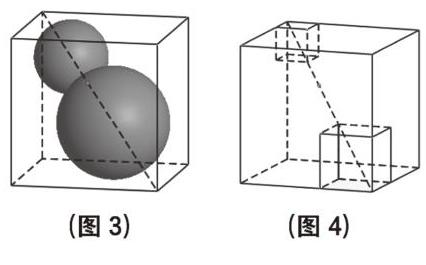
案例1 去年國慶假期的時候,我班的一個學生在班級微信群里發了一個水車的視頻(圖1),我感覺挺有創意的,于是我就想,我能否把這個水車的動畫做出來呢?經過認真地研究:我先在圓上取一點A,通過動畫功能使點A沿著圓周旋轉,并在點A處構造一個圓柱做成水車的一片“葉子”,通過迭代功能得到其它幾片“葉子”。為了增強作品的趣味性,我通過設置參數取值范圍,控制小人的頭、脖、腰、手、腳等的大小和長短(圖2)……。收假后我將作品拷到教室電腦里,當同學們看到時無不驚訝稱奇,為了進一步勾起學生的學習興趣,我讓幾個“膽大”的學生上臺修改“小人”的參數,“小人”身材夸張的變化引起了同學們的哄然大笑,同學們在感覺新奇的同時紛紛問我是怎么做到的,有的甚至躍躍欲試,就這樣,在調動學生學習興趣的同時,我又讓學生輕松地了解并掌握了平移、旋轉、對稱、伸縮等幾何做圖方法。
2.借助《幾何圖霸》的作圖功能,輕松實現數與形的相互轉換
數學的一個顯著特點就是抽象性,如何把抽象的數學語言、數量關系與直觀的幾何圖形,位置關系結合起來,這對于大部分學生來說都是比較困難的。我們可以利用《幾何圖霸》來解決這一難題,輕松實現以形助數,以數輔形,使許多復雜的數學問題簡單化。
案例2 已知棱長為2的正方體中,有2個小球相外切,并且這兩個小球與正方體各面均相切,則這兩個小球表面積之和的最小值為多少?
上述問題需要很強的空間想象能力和邏輯思維能力,如果沒有圖形輔助,學生是無從下手的,而手工又很難畫出跟球有關的圖形,教學時我引導學生利用《幾何圖霸》在正方體的體對角線上取一動點O,并設置點O的動畫功能,過點O向正方體的面作投影點A,以O為球心,OA長為半徑作好第一個小球,根據第一個球的作圖過程讓同學們討論如何作第二個球。做好圖形 (圖3)后,通過動畫功能使兩球兩球的大小和位置發生變化,就這樣通過生動形象的圖形使得抽象的知識變得趣味化、直觀化,讓學生在學習時,不再感到枯燥乏味,反而能夠使學生從學習中收獲成功的體驗。為了探究兩球的半徑與體對角線長的關系,我提示學生通過球與正方體各面的切點構造正方體(圖4),從而推出結論:( 3 +1)(r1+r2)=2 ?3 ,∴(r1+r2)=3- 3 再利用基本不等式求出兩球表面積之和:S=4π(r12+r22)≥2π(r1+r2)2=2π(3- 3)2,從而解決問題。就這樣,通過數形結合來解決問題,可以化難為易,不僅促進學生形象思維和抽象思維的協調發展,更促進了學生的可持續性發展。
3.借助《幾何圖霸》,突出重點,突破難點
在新授課時,利用《幾何圖霸》輔助教學,設置精彩動畫效果,不僅可以做到圖文并茂,還可以根據學生的思維發展水平與認知規律,結合動畫、漸變、迭代、度量、計算等功能將知識難點和事物的變化過程進行直觀演示,讓學生牢固地掌握知識體系的形成,促進形象思維向抽象思維發展,促進學生參與教學活動,加深對知識的理解和掌握,提高教學效率。
案例3 在學習旋轉體時,我通過動畫功能,向同學們演示圓柱的側面展開圖為矩形(圖5),由展開圖發現圓柱的側面積等于底面圓周長乘以圓柱的高,即S側=2πrh。又如圓錐的側面展開圖為扇形(圖6),扇形的半徑長為圓錐的母線長、扇形的弧長為圓錐底面圓周長,所以圓錐的側面積為扇形的面積,即S側=πrl.通過動畫演示學生對知識點一目了然,輕松掌握。
4.借助《幾何圖霸》變靜態教學為動態教學
德國詩人席勒曾說過:“活的形象最美,一塊玉石是無生命的,卻能由雕刻家賦予它生命,使人們在觀察中發現它的美”。藝術大師的作品往往善于化靜為動,化無生命之物為有生命之物,刻意去表現動態之美。教學是一門藝術。《幾何圖霸》則讓數學教學真正地實現藝術化,數學教師也可以把某些靜態問題當作動態過程的一個特定時刻加以考察,把一些靜止的圖形當作某種運動變化的結果來研究,展現數學世界中的動態之美。
案例4 已知正方體的棱長為1,每條棱所在直線與平面α所成的角都相等,則α截此正方體所得截面面積的最大值為 ? ? ? ? ? ?.
在問題分析過程中,由正方形的對邊分別平行我們可知,只需研究從A1引出的三條棱與平面α所成的角都相等即可,(圖7),此時,平面α截此正方體所得截面為正三角形。當截面上下平移時,通過動態的圖形發現當截面α由三角形變化到正六邊形(圖8)時,截面面積最大,并輕松求出截面面積的最大值。
總之,《幾何圖霸》能有效的彌補傳統教學方式、方法的不足,大大提升學生學習興趣、鍛煉數學思維能力,實現教學的高效性。但它的使用率仍然較低,在教學中的應用還處于初級階段,實踐教學之路仍然很漫長,但我相信,隨著信息技術的發展和教學改革的不斷深入,這款軟件一定會進入到每個課堂,讓每一個教師和學生受益。

