論初中數學教學中的變式訓練
廖文金

摘 要:本文圍繞初中數學教學展開論述,論述變式訓練在此方面教學工作中的運用問題。文章結合具體的題目對這一訓練方式所遵循的原則進行簡單介紹,并具體介紹集中訓練方法,希望能夠有效培養學生的數學核心素養。
關鍵詞:初中數學;數學教學;變式訓練
引言
初中階段的數學基礎知識相對較少,其題目的設置總是圍繞某一知識點或某一重點題型,但學生在解答時仍會手足無措,這主要是由于學生缺乏這樣針對性的訓練,發散思維能力薄弱,這不利于學生數學核心素養的培養。應用變式訓練于課堂教學能夠有效改善這一問題,文章將圍繞這一點展開。
一、變式訓練所遵循的原則介紹
(一)可行性原則
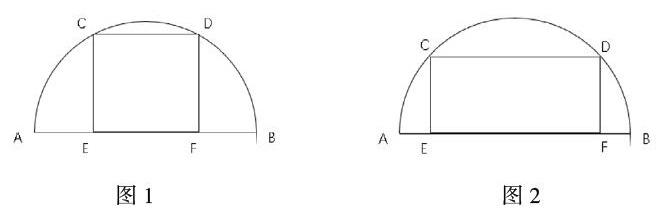
在進行變式訓練時,教師要考慮到可行性,能夠實現變式訓練是需要教師對相關題目進行巧妙合理的轉變,引導學生思維發散,培養其“舉一反三”的能力,進而培養其數學思維,促進其數學核心素養的提升。以下述題目為例,如圖1,有一塊半圓形材料,現需從中截取一個正方形,要求截取正方形的一邊要在AB邊上,其中AB為10,即就是半圓的直徑,現需求所截正方形的邊長域面積。那么,教師就可根據此題進行簡單的變式訓練,將題目中的正方形換成矩形,其余條件不予改變,要求學生計算相應矩形的邊長與面積,如圖2。利用圖形的簡單轉化,實際這樣還加大了題目難度,這樣的題目變式訓練能夠有效訓練學生的數學思維。
(二)針對性原則
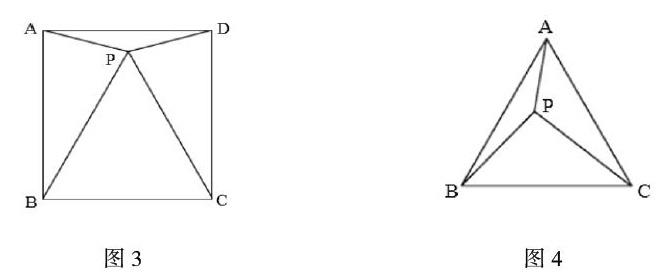
初中階段的數學基礎性內容并不多,變式訓練的目的是為了讓學生對相應數學問題的本質達到融會貫通的目的,使其能夠熟練運用數學知識解決實際問題,因此,教師在教學過程中,要有針對性地進行變式訓練,充分發揮變式訓練的作用[1]。以下述題目為例,如圖3,正方形ABCD中有一點P,其中∠PAD和∠PDA均為15°,求證三角形PBC為等邊三角形。其主要利用正方形的特性和角度進行求證。基于此,教師可借助等邊三角形的特性,將題目進行轉化,如圖4,三角形ABC是等邊三角形,而P位于三角形內部,PA、PB、PC三邊分別為3、4、5,求∠APB。問題的本質都是利用幾何圖形的特性與度數求解問題,如此教學,可有效培養學生的數學思維,對其解答幾何證明題目意義重大。
二、具體訓練方法分析
(一)圍繞基礎概念進行變式訓練
初中階段的數學概念相對較多,并且在解題中應用也十分頻繁。尤其是在幾何證明部分,相應幾何體的性質是重要考點,也是學生容易混淆的部分。例如,矩形是特殊的平行四邊形,菱形是特殊的平行四邊形,而正方形又是特殊的菱形,但其又具有矩形的性質。這些幾何圖形都是由矩形轉化得到的,在一些幾何證明題中通常需要對這些幾何圖形的概念和性質進行正推與反推,這是初中階段幾何證明類題目的主流。教師在概念的講解過程中要注意運用簡單的變式訓練,以促進學生對相應概念的理解,達到融會貫通的目的。這樣學生在解答數學題目中就可以理清概念,做到思路清晰,邏輯嚴密。
(二)圍繞典型題目進行變式訓練
以初中階段的追逐與相遇問題為例,比如,小明和小華相距20公里,兩人分別乘坐不同的交通工具,小明乘坐小轎車以每小時50公里的速度出發,小華騎自行車以每小時25公里的速度出發,問:經過多長時間,兩人能夠相遇?這一問題在初中階段的實際應用題目中十分常見。教師可基于此類問題進行變式訓練,將相遇變為相距。以上述題目為例,繼續設問,基于上述條件,問他們第一次相遇后,多長時間兩人相距20公里。當然也可以將問題進行轉化,轉為追逐類題目。假設兩人在環形跑道起點同時同向出發,小明以每分鐘300米速度出發,小華則以每分鐘400米的速度出發,問二人出發后經過多長時間,小華能夠領先小明一整圈?這一問題的實質和上述的題目是相同的,教師對此類問題進行簡單的變式訓練,引導學生熟練掌握這類問題[2]。
(三)圍繞創新型題目進行變式訓練
數學習題中有一些特別典型的題目,其是在傳統題目上進行創新,考察學生的數學創新思維,教師可將這類題目篩選出來進行變式訓練,培養學生的數學創新思維。以下述題目為例,如圖5,ABCD為正方形,其邊長為1,P為其內一點,問PA+PB+PC的最小值。基于這一類目,教師可進行簡單的轉變,改為逆向求解類題目。如圖6,正方形ABCD,P為其內一點,已知,PA、PB、PC分別為1、2、3,問正方向的邊長。這樣的變式訓練,將問題與條件調換位置,能夠充分培養學生逆向思維和創新思維,提升其數學核心素養,充分發揮變式訓練的作用,提高學生數學能力。
三、結束語
教師要正視初中數學的現狀,在教學過程中要遵循可行性原則和針對性原則,確保變式訓練在教學中有效落實。教師可圍繞基礎概念、典型題目,創新型題目進行變式訓練,有效培養學生數學思維,提高其數學能力,促進其數學核心素養的提升。
參考文獻:
[1]周凌鶴.淺談初中數學教學中變式訓練設計策略[J].考試周刊, 2017(65).
[2]周豪.初中數學教學中變式訓練設計策略探究[J].科教導刊-電子版(下旬), 2019(4).

