小學數學教學中教師創設情境培養學生轉化意識的方法分析

摘 要：在小學數學教學中不僅要讓學生獲得能夠適應社會生活和進一步發展所必需的基礎知識、基本技能，還應讓學生獲得必備的基本思想方法。轉化思想是學生連接新舊知識、解決數學問題的必備思想方法，教師在教學過程中要努力創設情境，培養學生的轉化意識，使學生養成自主轉化的習慣。

關鍵詞：轉化;創設情境;解決問題

學生在數學學習中不僅要掌握必備的基礎知識和基本技能，更要學會運用數學的眼光和思維解決實際問題。讓學生學會根據已有知識，從實際背景中抽象出數學問題，構建數學模型，解決問題是數學學習的關鍵。

小學數學中轉化思想是指把生疏問題轉化為熟悉問題，將抽象的問題轉化為具體的和直觀的問題;將復雜的問題轉化為簡單的問題，將實際問題轉化為數學問題等，從而使問題易于解決。它是數學學習過程中最常用的思想方法，是數學問題解決的基本思路和途徑之一。教師數學教學過程中應讓學生養成自覺轉化的習慣，提高學生解決問題的能力。下面就以“三角形的面積”一課為例，談談如何利用轉化思想，提高學生解決問題的能力。

一、 挖掘生活資源，轉化成數學問題

現實生活中蘊涵著大量與數量和圖形有關的問題，教師要引導學生把這些問題抽象成數學問題，用數學的方法加以解決。在這過程中，就需要引導學生樹立敏銳的數學應用意識，主動把現實生活中的問題轉化成數學問題，進行探究，以找到解決問題的突破口。

環節一：談話中引入

成為一名少先隊員后，我們每個人都要佩戴紅領巾。紅領巾是什么形狀的，如果要想知道它用多少面料，要怎樣解決呢？

從學生熟知的紅領巾入手，讓孩子對知識產生親切感，順利引領大家把現實問題轉化成數學問題，找到解決實際問題的突破口，從而順利轉入新知的學習。

二、 聯系已有知識，轉化成數學猜想

在學習“三角形面積”之前，學生已經掌握了平行四邊形面積的推導方法，也就是說學生已經積累了把未知圖形面積轉化成已知圖形面積的一種方法，并且理解了其中的數學思考方法。當學生遇到求三角形面積時，就能根據已有知識進行合理猜測。

環節二：追問促猜想

追問：怎樣求三角形的面積？

你能回憶一下平行四邊形公式的推導過程嗎？

大膽猜測一下，可以把三角形轉化成我們已經學過的哪些圖形？

（可以把三角形轉化成長方形，可以把三角形轉化成正方形，可以把三角形轉化成平行四邊形？）

通過回憶喚醒學生已有知識，引導學生大膽猜測，讓孩子養成碰到問題能主動聯系已有知識進行大膽猜測，然后進行實踐驗證的習慣。

三、 參與實際操作，轉化中解決問題

學生知識的獲得不能依賴死記硬背，而應以理解為基礎，讓學生主動參與實踐操作，把思維和行動融合在一起，

這樣才能不斷地驗證自己的猜想，找到最佳的問題解決策略，為今后解決實際問題奠定基礎。

環節三：小組合作促轉化

1. 材料包

鈍角三角形、銳角三角形、普通直角三角形、等腰直角三角形各4個，剪刀、直尺等。

2. 思考

計劃把三角形轉化成哪個猜想的圖形？在轉化過程中用了幾個三角形？

如果是一個三角形，你們怎么轉化，如果是兩個又怎么轉化？……轉化后圖形與原三角形又有什么關系？

3. 操作過程中，填好相應的學習單

我們是用（? ）個（? ）三角形，通過（? ）轉化成了一個（? ）。

原三角形的底等于轉化后（? ）形的（? ）;原三角形的高等于轉化后（? ）形的（? ）;原三角形的面積等于轉化后（? ）形的（? ）。

教師要給予充足的材料，讓學生有更多的探索空間，讓他們在合作中主動參與、提出各自解決方法，并在與他人的交流合作中選擇合適的策略，豐富數學活動的經驗，碰撞出思維的火花，提高思維水平。

環節四：轉化圖形的呈現

教師給學生充足的表達空間，培養他們的語言表達能力、傾聽能力、辨思能力，讓其找到別人解決問題的關鍵之處，也讓孩子們發現更多解決的方法，以拓寬自己的思維。

轉化類型倍拼法割補法折疊法

正方形

長方形

平行四邊形

發現：平行四邊形通過沿高剪切，然后平移可以轉化成長方形，但由于三角形在分割的時候無法沿用平行四邊形的剪切方法，因此大部分組都采用的是倍拼法，割補法只有少數組運用。

沒有學生應用折疊法，老師可以展示這一方法，為他們的思維開拓一條新路。

割補法和折疊法的展示激發了孩子們探究的興趣，引發了學生自主操作，提高了學生的推理能力。思維的發展是一個不斷遞進的過程，只有當孩子在經歷長期的不斷反思、不斷質疑、不斷改進中才能得到逐步的提升。

環節五：對應量的轉化

根據轉化圖形推導出三角形面積公式。

在解決問題的過程中，我們要在粗獷的線條中，尋找細膩的支點，從而找準圖形對應量之間的關系，準確推導出三角形的面積公式，這是學生知其所以然的關鍵，也是學生獲得最終成功喜悅的關鍵。

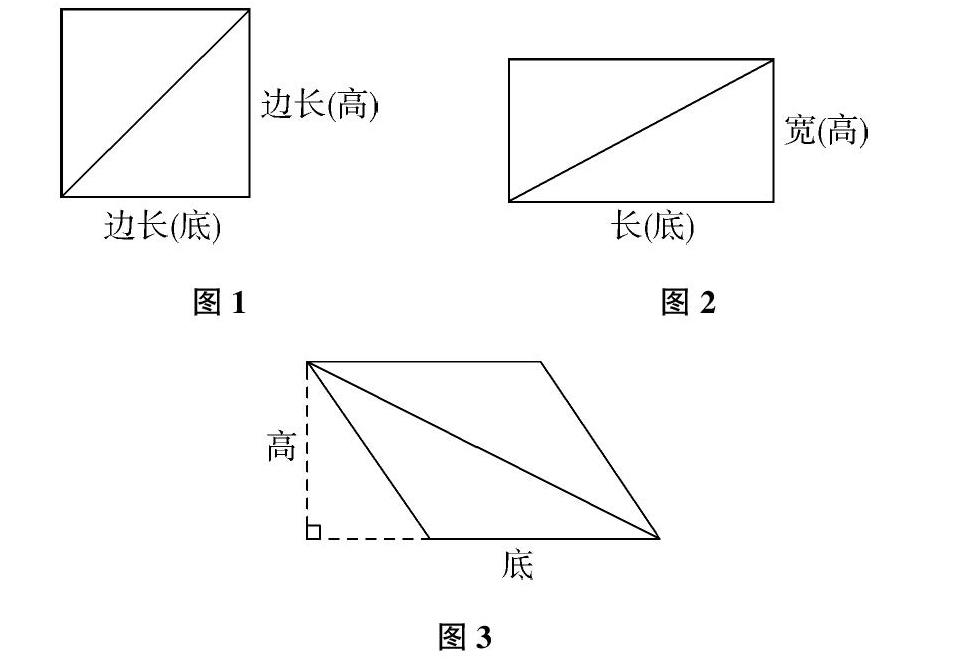
圖1拼成的正方形的邊長等于原三角形的底，邊長等于原三角形的高。

圖2拼成的長方形的長等于原三角形的底，寬等于原三角形的高。

圖3拼成的平行四邊形的底等于原三角形的底，高等于原三角形的高。

所以推導出三角形的面積=底×高÷2

圖4拼成的長方形的長等于原三角形的底，寬等于原三角形高的一半。

圖5拼成的平行四邊形的底等于原三角形的底，高等于原三角形的高的一半。

由圖4圖5可以得出：三角形的面積=底×（高÷2）

推導出：三角形的面積=底×高÷2

圖6折出的長方形面積是三角形面積的一半，長和寬也分別是三角形底和高的一半。

三角形的面積=（底÷2）×（高÷2）×2

推導出：三角形的面積=底×高÷2

用字母表示S=ah÷2

教學是一個循序漸進的過程，教師不僅要讓學生掌握結果呈現的知識，更應重視學生思維的形成過程，這樣才能提高學生的探究意識、應用意識和創新意識。在上面的轉化推導過程中，使學生知道了結果，也感悟了結果產生的原因。

四、 對比今古思維，感受轉化魅力

在悠久燦爛的中國古代文化中，數學文化是其中一朵絢麗的奇葩，它是古代科學的基石，是中華文化不可缺少的一部分，其充分展示了古代勞動人民的聰明才智。在兩千多年前人們就熟練掌握了轉化的方法，并將其用之于實際生活中，為人類社會生活以及社會進步做出了重要的貢獻。轉化思想在人類歷史長河中，在各個方面的發展中都起著重要的作用。

環節六：閱讀中感悟

現在我們通過幾種方法推導出了三角形的面積公式，你們知道古代人們是怎樣計算三角形面積的嗎？

在閱讀中讓學生產生思維的碰撞，感受古代勞動人民的偉大，感受古今方法的相通之處，知識的轉化是解決問題的關鍵，教師要讓他們發現我們在前人的基礎上開拓了新思路，有了新方法。

五、 比較不同轉化，找到最佳策略

我們在追求思維廣度和方法多樣化的同時，也要讓學生在比較中感受方法的簡單化。

環節七：質疑中強化

追問：1. 我們可以用這么多種方法推導出三角形的面積公式，為什么書本上只用了“倍拼法”？

2. “倍拼法”中三角形和所拼成的平行四邊形什么關系？

引導得出：三角形的面積等于等底等高平行四邊形面積的一半。強化“等底等高”，加深學生對三角形面積公式中“÷2”的理解。

通過運用上面三種不同方法推導得出公式，學生自然發現“倍拼法”得出的三角形面積公式最為簡單。簡單化是數學最基本、最顯著的一個特征和方法。數學學習追求思維的簡單，形式的簡單，解決問題的簡單。為什么我們要推導出三角形的面積公式呢？這是因為數學不僅要追求簡單化，也要追求統一性，建立數學模型，使大家能用最簡潔的方法解決三角形的面積問題。在三角形的面積計算時“÷2”是學生最容易遺漏之處，教學時，教師不僅要讓孩子們在數形結合中理解“÷2”的意義，也要反復強調，多次練習鞏固。

六、 利用新知，解決實際問題

環節八：鞏固促轉化

獲取知識最終是要去解決相應問題的，只有這樣才能體現學習的價值，在通過轉化推導得到三角形的面積公式后，教師應讓學生把所學的知識再應用到實際問題中，激發學生的學習熱情，讓其感受成功的喜悅，提高學習數學的積極性。同時在解決實際問題的過程中，要引導學生進一步鞏固所學的知識，為下一次知識的轉化做好準備。

1. 小組測量紅領巾底和高，求紅領巾面積

測量過程中感受三角形的底和高必須相對應，感受探索成功的喜悅，激發學生學習的積極性。

2. 下圖中哪個三角形面積與三角形ABC面積相等，為什么？

在題2的解決過程中，又一次實現了知識的完美轉化，讓學生明白三角形的面積大小不受形狀的影響，只與三角形的底和高有關，得出“等底等高三角形的面積相等”的結論。

教學是一個逐步完善的過程，學生的學習也是一個逐步進步，緩慢上升的過程。教師要努力在教學中為學生創設教學情境，激發他們的學習熱情，使他們全身心地投入教師精心組織的教學活動中，這樣學生才能在數學思考、問題解決和情感態度等方面得到發展。

參考文獻：

[1]義務教育數學課程標準（2011年版）[S].中華人民共和國教育部，2012（6）.

[2]劉超.從沖突質疑走向深入思考[J].小數數學教師，2021（6）.

[3]吉智深.在比較和對比中培養學生發現問題并提出問題的能力[J].小學數學教師，2020（4）.

[4]李惠玲.以“問題串”為主線，凸顯知識本質[J].中小學數學，2021（1）.

作者簡介：湯金紅，浙江省杭州市，浙江省杭州市蕭山區高橋小學。