讓思維導圖“導”出學生思維的靈氣

何正鋒

【摘要】通過思維導圖的應用能夠全面地調動左腦對邏輯、順序、條例、文字、數字以及調動右腦對圖像、想象、顏色、空間、整體等的思維，使得大腦的潛能和創造力得到最充分的開發，從而極大地充分激發人們的科學創造性和思維能力。思維導圖的應用于我國小學和初中數學的教學中既完全具備了學習方法和工具的強大實用性和優勢，又充分符合了小學生的學習思維過程和創造性認知的特點。

【關鍵詞】思維導圖;小學數學;思維能力

波利亞認為，教師要把三分之一的努力花在學生教些基本的數學上，而把三分之二的努力花在培養對學生有益的數學思維表達方法和良好的思維習慣上。精彩的課堂數學和思維課堂教育不一定要強調教學形式如何新穎，內容如何豐滿，當教師能夠引領學生在精彩的數學和思維的世界里自由遨游時，我們的基本數學思維在課堂就已經可以說明它是有效的、深刻的、靈動的。那么，如何才能實現？用思維導向圖可以實現我們這個愿望。思維導圖是二十世紀英國著名學者東尼·博贊（tonybuzan）在20世紀60年代所創的一種新型記憶與思維方法。它主要是表達各種發散性抽象思維的有效工具，可應用于所有認知功能領域，尤其是記憶、創造、學習和各種形式的抽象思考，它被研究者描述為“大腦的瑞士軍刀”。它既可以是呈現數學知識的網絡，是間接組織學生陳述抽象性知識的良好工具，同時也可以直接呈現思維過程，是組織程序性知識的良好工具。思維導圖工具應用于我國中小學數學的教學中既完全具備了學習思維導圖工具的強大功能和優勢，又充分符合了中小學生的學習具體思維過程和其認知特點。一方面，思維導圖可以通過圖像、色彩等手段，把難于表達的隱性數學知識轉化成一種形象化的顯性數學知識，使得中小學生在學的具體思維過程中完全能夠很好地理解和領悟隱性的知識。另一方面，學生在自主學習的過程中，可以通過思維導圖自主地建構知識結構，加工整理數學概念，參與組織數學抽象性問題的分析和討論，做到對于數學知識的深入系統理解和有效運用，培養小學生形象思維的能力和對信息處理的能力，以新的高度有效地充分開發小學生的思維潛力。在小學數學教學中，學生思維形象極其活躍，有利于教師在教學中引入思維導向圖來輔助教學。

一、“導”出學生思維的發散性

發散性的思維圖模式又稱發散性輻射求異思維或發散性求異思維，是指學生的大腦在發散性思維時呈現出一種高度擴散和延展狀態的思維導向圖模式，從一個目標或者事物的思維中心或者起點開始出發，沿著不同的方向，各個的角度向學生提出各種的設想，尋找各種的途徑，解決具體的問題。而發散性思維的導向圖模式能讓學生用發散性的思維把每一個人的想法都按需要從一個思維中心或者主題方向放射出去，進行360度全方位的輻射和多角度的延展。

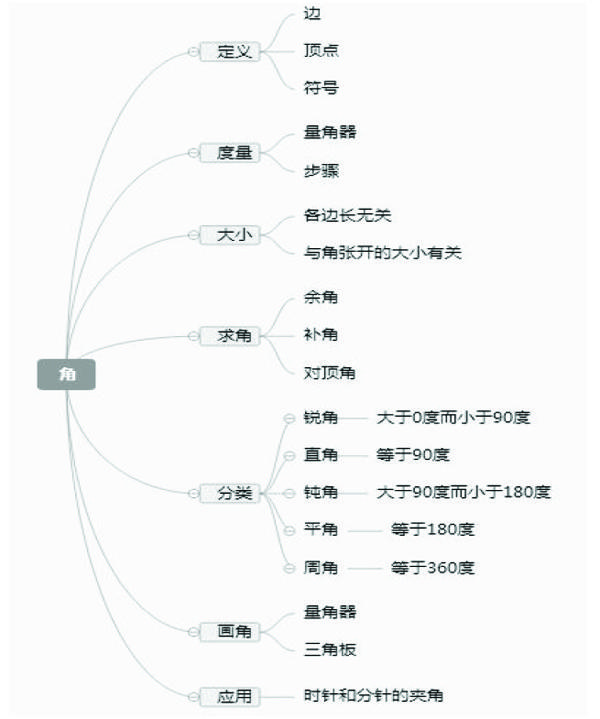
教師引導學生在整理和復習《角》的思維聯想相關內容和知識的時候，先引導學生提出一個聯想的關鍵詞——角，然后可以引導其他學生盡興地思考這個聯想的關鍵詞，把自己需要聯想的關鍵詞和內容分成幾個版塊記錄下來，再按照聯想的版塊一級一級地進行各個分支的聯想，能夠進行聯想得到多少就能夠進行聯想得到多少。學生可以與其他同學進行商量，向教師和學生尋求聯想上的幫助，完善自己的聯想和思維導圖。在課堂教學中，有一位學生繪制了下面的聯想和思維導圖。從這幅思維導圖中，我們可以清楚地看出，學生在導圖繪制時的思維發散導圖過程，越是層層往下，分支越多，聯想得到的關鍵詞和內容也就越多。值得一提的是，在“應用”版塊，學生已經能聯想到“九點整”“六點整”“一點整”等一系列更深層次的思維導圖問題。可見，對學生的思維導圖發散的能力非常強。思維導圖促進了學生的“學”和教師的“教”，為學生提供了一種積極活躍的探討氛圍，以發散性的思維激發學生的興趣，以圖示的方式給學生提供了無限遐想的思維空間。

二、“導”出學生思維的獨創性

思維導圖在解決問題中運用的是“數形結合”的思想。作為數學思維，數形結合的應用就是借助于形的幾何直觀性來闡明數之間的某種關系。因此，在教學實踐中，學生獨立聯想和繪制思維導圖的繪制過程就是學生自主創造的一種實踐過程，學生需要具有廣泛獨立聯想的思維能力，可以根據自己的興趣喜好自由設計繪制符合條件的各種思維方法和導圖。在對思維想法和導圖的設計繪制和展示過程中，學生先要對問題進行大量的思考，然后把自己頭腦中產生和迸發出的各種思維想法，用文字和圖畫的各種表現方式完美地組合在一起。當學生在課堂中構建自己的獨立聯想思維方法和導圖后，與其他教師對學生的思維作品內容進行了比較時，還可能會產生新的思維想法，這樣就有利于更好地培養和提高學生的自主創新探索精神和自主實踐的能力。教師和學生的繪制和認識思維過程實際上是由學生感性到理性再到感性循環往復、螺旋上升的一個過程，為此，學生通過對思維導向圖的繪制和展示可以更好地幫助教師和學生在更高的層次上引導學生展開有理有據的探索和思辨，提高主動地應用所學知識主動解決實際問題的意識和能力，讓教師和學生的繪制思維導圖變得更具獨創性。

三、“導”出學生數學模型建構

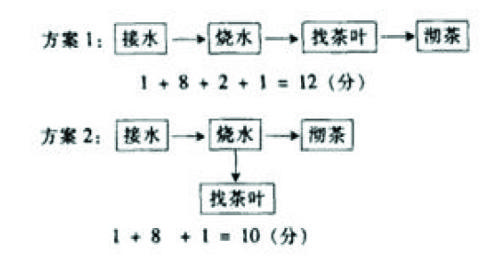
教師要立足于學生已有的知識和生活經驗，引導學生親歷學習過程，將實際問題抽象成數學模型并進行解釋與應用，讓學生獲得發現和解決數學問題的機會，讓學生能夠通過“經歷”和“體驗"”來了解數學思想和模型理論建構的具體形成和應用過程，因為具體可操作性強可以清楚地讓學生了解四年級的學生通過什么樣的數學活動、什么思維方式可以獲得數學知識技能及其思想方法。在教學人教版四年級上冊《沏茶問題》的過程中，以平時已經幫家里做了大量的家務，有一定的家庭生活經驗的四年級的學生作為課堂教學的起點，把一個學生自己比較熟悉的“沏茶”問題作為教學的引例，通過自己設計學生沏茶活動的順序和時間，再通過與同學的交流，便有了學生初步的體會。教師不僅要引導學生考慮做一件事情的時間安排和順序還要引導學生考慮自己是否可以“同時做”這兩個問題思維的方式和角度。學生可以通過用數學思維的導向圖對學生進行觀察和比較為什么同樣可以增加一件新的事情，一種方案的增加時間為什么不變，而另一種方案的增加時間為什么變了呢？

通過觀察和橫向的比較，讓學生進一步體會到兩件事情橫向發展的順序和我們同時可以做的兩種事情思維方式和角度的不同，所以我們花的時間也可能會隨著不同。通過對觀察和縱向的比較和分析，讓學生進一步地明白，我們同時可以一起完成的兩件事情越多，那么越可能節省時間的基本道理。學生也從中形成了自己的知識體系，建立自己的時間管理模型。

思維導圖的出現讓數學不再冷冷清清，不再是單調乏味，而是色彩繽紛，猶如游走在藝術之境，讓我們締造美、欣賞美、使用美。思維導圖促進了學生的“學”和教師的“教”，為師生提供了一種積極活躍的探討氛圍，打破了學生的思維定式，借助思維導圖這“大腦使用的說明書”，讓學生徹底愛上數學，愛上思維，需要我們去努力挖掘、探討、研究，以圖示的方式給學生提供了無限遐想的思維空間，讓學生在學習中體驗到學習的快樂。

參考文獻：

[1]東尼·博贊.教學思維模式導圖：讓您了解你的大腦如何靈活使用的一本說明書[M].外語教學與研究出版社，2002.

[2]劉艷.你一旦開學就有機會的現代英語教學思維模式導圖[M].大學中國語言文化與經濟發展社會科學技術研究出版社，2017.