運(yùn)用轉(zhuǎn)化思想進(jìn)行分?jǐn)?shù)計(jì)算教學(xué)

勞雅利

【摘? 要】著名數(shù)學(xué)家、莫斯科大學(xué)教授C.A.雅潔卡婭在一次《什么叫解題》的演講時(shí)說(shuō)：“解題就是把要解題轉(zhuǎn)化為已經(jīng)解過(guò)的題。”在分?jǐn)?shù)計(jì)算教學(xué)中教師要有機(jī)滲透轉(zhuǎn)化思想，如：數(shù)與形轉(zhuǎn)化，等量轉(zhuǎn)化，化繁為簡(jiǎn)等，逐步培養(yǎng)學(xué)生把復(fù)雜問(wèn)題轉(zhuǎn)化為簡(jiǎn)單問(wèn)題，把新學(xué)知識(shí)轉(zhuǎn)化為已學(xué)知識(shí)，使學(xué)生在解題過(guò)程中站得更高遠(yuǎn)、看得更清晰、想得更絕妙。

【關(guān)鍵詞】轉(zhuǎn)化;數(shù)與形;繁;簡(jiǎn);等量;新知;舊知

數(shù)學(xué)思想是數(shù)學(xué)的精髓和靈魂，轉(zhuǎn)化思想是數(shù)學(xué)思想的重要組成部分。它可將數(shù)學(xué)問(wèn)題化難為易、化繁為簡(jiǎn)，把一個(gè)復(fù)雜問(wèn)題轉(zhuǎn)化為一個(gè)簡(jiǎn)單問(wèn)題，把一個(gè)不熟悉的問(wèn)題轉(zhuǎn)化為熟悉的問(wèn)題，從而實(shí)現(xiàn)新知識(shí)向舊知識(shí)轉(zhuǎn)化的目標(biāo)。

分?jǐn)?shù)計(jì)算在小學(xué)計(jì)算教學(xué)中占有很大的比重，它的掌握是學(xué)生進(jìn)一步學(xué)習(xí)的重要基礎(chǔ)。數(shù)學(xué)轉(zhuǎn)化既包含了數(shù)學(xué)特有的數(shù)、式、形的相互轉(zhuǎn)換，又包含了心理達(dá)標(biāo)的轉(zhuǎn)換。轉(zhuǎn)化的目的是不斷發(fā)現(xiàn)問(wèn)題、分析問(wèn)題和最終解決問(wèn)題。下面結(jié)合本人多年的教學(xué)實(shí)踐，談?wù)劮謹(jǐn)?shù)計(jì)算教學(xué)中常見(jiàn)的基本轉(zhuǎn)化類(lèi)型和轉(zhuǎn)化方法。

一、數(shù)與形轉(zhuǎn)化的思想

著名的數(shù)學(xué)家華羅庚先生指出：“數(shù)缺形時(shí)少直覺(jué)，形少數(shù)時(shí)難入微，數(shù)形結(jié)合百般好，隔裂分家萬(wàn)事休。”就是說(shuō)，數(shù)缺形時(shí)少直觀，形少數(shù)時(shí)難刻畫(huà)。因此，我們教師應(yīng)重視數(shù)與形的結(jié)合與轉(zhuǎn)化，以形助數(shù)，以數(shù)輔形，把數(shù)學(xué)問(wèn)題中的運(yùn)算、數(shù)量關(guān)系等與幾何圖形與圖像結(jié)合起來(lái)進(jìn)行思考，從而使“數(shù)”與“形”各展其長(zhǎng)，優(yōu)勢(shì)互補(bǔ)，相輔相成，不僅提高了學(xué)生計(jì)算技能，而且使邏輯思維與形象思維完美的統(tǒng)一起來(lái)。

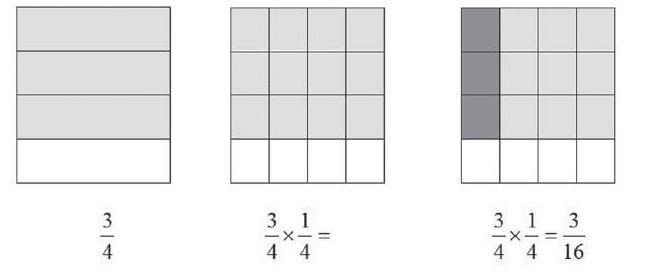
例如在教學(xué)分?jǐn)?shù)乘法的教學(xué)中，如下教學(xué)設(shè)計(jì)：

1.出示問(wèn)題

2.利用手中的長(zhǎng)方形紙獨(dú)立思考，表示出? ? ?的? ? 是多少？

3.小組及全班交流，根據(jù)學(xué)生畫(huà)的圖依次展示下面的過(guò)程。

“數(shù)”與“形”的信息轉(zhuǎn)換，相互滲透，不僅使解題簡(jiǎn)捷明快，還開(kāi)拓解題思路，為研究和探求數(shù)學(xué)問(wèn)題開(kāi)辟了一條重要的途徑。由此，教師應(yīng)努力探索，引導(dǎo)學(xué)生通過(guò)“數(shù)”與“形”的相互轉(zhuǎn)化，使其既知其然又知其所以然。探索出一條合理的解題途徑，解決學(xué)生心中存在的困惑，培養(yǎng)學(xué)生的數(shù)學(xué)能力。

二、生疏向熟悉轉(zhuǎn)化的思想

生疏問(wèn)題向熟悉問(wèn)題轉(zhuǎn)化是解題中常用的思考方法。解題能力實(shí)際上是一種創(chuàng)造性的思維能力，這種能力的關(guān)鍵是能否細(xì)心觀察，運(yùn)用過(guò)去所學(xué)的知識(shí)，把新知識(shí)轉(zhuǎn)化為舊知識(shí)，將生疏問(wèn)題轉(zhuǎn)化熟悉問(wèn)題，這也是一個(gè)很重要的數(shù)學(xué)思想。

我們教師應(yīng)深刻挖掘量變因素，將教材抽象、加工，縮小學(xué)生接觸新內(nèi)容時(shí)的陌生度，這樣做常可起到事半功倍的效果。

例如在分?jǐn)?shù)除法的教學(xué)中，可以數(shù)形結(jié)合進(jìn)行教學(xué)，也可以如下設(shè)計(jì)：

1.首先出示口算準(zhǔn)備題：? ? ? ? ? ? ? ? ? ? ? ? ? ?（60×5）÷（5×5）=

2.出示? ? ? ? ? ?，然后提示學(xué)生可不可以轉(zhuǎn)化為我們熟悉的題目。

3.根據(jù)學(xué)生的思考，可以進(jìn)行以下的轉(zhuǎn)化

（1）可以利用商不變性質(zhì)把被除數(shù)轉(zhuǎn)化為“1”進(jìn)行計(jì)算

（2）可以利用商不變性質(zhì)把除數(shù)轉(zhuǎn)化為“1”進(jìn)行計(jì)算

4.根據(jù)學(xué)生的列式比較討論哪個(gè)方法更好，是否可以推廣到其他的分?jǐn)?shù)除法中，并舉例說(shuō)明。

5.小結(jié)：一個(gè)數(shù)除以分?jǐn)?shù)等于一個(gè)數(shù)乘以這個(gè)數(shù)的倒數(shù)

這節(jié)枯燥的數(shù)學(xué)課在這種轉(zhuǎn)化思想的指引下，學(xué)生學(xué)得有趣、輕松，同時(shí)還把整數(shù)除以分?jǐn)?shù)和分?jǐn)?shù)除以分?jǐn)?shù)兩節(jié)課的內(nèi)容在一課時(shí)中就很自然得完成了，并取得了較好的教學(xué)效果。

生疏的轉(zhuǎn)化成熟悉的或熟悉的生活事例抽象成數(shù)學(xué)運(yùn)算規(guī)律，這樣形成的知識(shí)是生長(zhǎng)在原有的知識(shí)土壤中，接受的知識(shí)是有根之木，也就更有生命力，不僅僅是授之“魚(yú)”，更是授之以“漁”。

三、化繁為簡(jiǎn)的思想

教育家加里寧說(shuō)：“數(shù)學(xué)是思維的體操。”學(xué)數(shù)學(xué)，是在學(xué)習(xí)一種化繁為簡(jiǎn)、邏輯性嚴(yán)密的數(shù)學(xué)思想，數(shù)學(xué)其實(shí)質(zhì)上是一種化繁為簡(jiǎn)，化難為易的數(shù)學(xué)轉(zhuǎn)化思想的具體體現(xiàn)， 可以達(dá)到熔化難點(diǎn)， 加快解題速度，提高計(jì)算正確率，起到事半功倍之效。

例如在2008÷2008? ?這一題的教學(xué)中，除數(shù)是這么大的帶分?jǐn)?shù)，如果直接把它化成假分?jǐn)?shù)，既麻煩又容易出錯(cuò)，那是肯定不行的，當(dāng)仔細(xì)觀察發(fā)現(xiàn)被除數(shù)和除數(shù)都有相同的數(shù)2008，運(yùn)用商不變的性質(zhì)簡(jiǎn)化數(shù)據(jù)，即化為1÷1? ? ? ? 計(jì)算就簡(jiǎn)單多了。

再如以下分?jǐn)?shù)也都可運(yùn)用分?jǐn)?shù)的基本性質(zhì)化繁為簡(jiǎn)：

四、等量代換的思想

有些看似簡(jiǎn)單的題目學(xué)生卻無(wú)從下手，我們教師要適時(shí)引導(dǎo)學(xué)生根據(jù)已知條件與未知條件之間的關(guān)系，把幾個(gè)未知條件轉(zhuǎn)化替換為已知條件或同一個(gè)未知條件，這樣等量代換就能輕松解決問(wèn)題。等量代換的思考方法在分?jǐn)?shù)教學(xué)中會(huì)經(jīng)常用到，讓學(xué)生換一個(gè)角度去思考，換一種思路去理解，逐步掌握轉(zhuǎn)化策略，提高靈活解題能力。

例如：已知甲×? ? ? =乙×? ? ?=丙×? ? ?，甲+乙+丙=480，甲、乙、丙分別是多少？這題有3個(gè)未知量，直接解答無(wú)從著手，如果把甲、丙都代換成乙，甲=乙×? ? ?，丙=乙×? ? ? ?，再根據(jù)甲+乙+丙=480代入，接下來(lái)就迎刃而解了。

“數(shù)學(xué)思想是數(shù)學(xué)的靈魂，數(shù)學(xué)方法是數(shù)學(xué)的行為。”當(dāng)學(xué)生有了轉(zhuǎn)化的思想就會(huì)遷移到實(shí)際問(wèn)題中去，遇到疑難問(wèn)題他們就會(huì)想辦法應(yīng)用這種思想來(lái)解決。這樣有利提高學(xué)生計(jì)算技能，培養(yǎng)學(xué)生的數(shù)學(xué)學(xué)習(xí)能力，拓展學(xué)生思維，提升學(xué)生數(shù)學(xué)綜合素養(yǎng)。