“植樹問題”教學設計

林宏

[摘 要]以數學課程標準和學情為依據，采用先學后教的教學模式對“植樹問題”進行再設計，突出數學思想的滲透，模型的建構和學生數學核心素養的提升。

[關鍵詞]植樹問題;數學思想;核心素養

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2021）20-0058-04

【教學內容】 青島版教材四年級上冊“智慧廣場”（第106頁～第107頁）。

【教材分析】

《義務教育數學課程標準（2011年版）》強調：要從學生已有的生活經驗出發，讓學生親身經歷將實際問題抽象成數學模型，并進行解釋與應用的過程。進而使學生獲得對數學理解的同時，在思維能力、情感態度與價值觀等方面得到進步和發展。根據課程標準的要求，“智慧廣場”的教學目標可概括為以下四點：

1.感悟重要的數學思想方法。

2.運用數學的思維方式進行思考，增強分析和解決問題的能力。

3.提高學習數學的興趣，增強學好數學的信心，養成良好的學習習慣，具有初步的創新意識。

4.在參與觀察、猜測、試驗、推理等數學活動中發展合情推理能力，感悟演繹推理思想，學會獨立思考。

教材編排了“兩端都栽時，間隔數和棵樹關系”“一端不栽時，間隔數和棵樹關系”“ 兩端都不栽時，間隔數和棵樹關系”三種不同的情況，并以學生比較熟悉的植樹活動為線索，讓學生選用自己喜歡的方法來探究栽樹的棵數與間隔數之間的關系，經歷猜想、實驗、推理等數學探索過程，并啟發學生透過現象發現規律、建立模型，再回歸生活，利用規律解決生活中的實際問題。

【學情分析】

四年級學生仍以形象思維為主，但抽象思維能力有了初步的發展，他們具備了一定的分析綜合、抽象概括、梳理規律的數學活動經驗。“植樹問題”放在這個學段，說明其具有很強的探究空間，需要教師的有效引領和學生的自主探究。

【教學目標】

1.經歷將實際問題抽象出數學模型的過程，掌握植樹問題中棵樹與間隔數之間的關系，并能利用這一關系解決簡單的實際問題。

2.經歷觀察、猜測、驗證、推理等解決問題的過程，體驗數形結合、一一對應、模型思想等數學思想方法。

3.感受數學在日常生活中的廣泛應用，體會數學的價值，產生熱愛數學的情感。

【教學重點】

引導學生發現棵數與間隔數之間的關系，使學生經歷探究過程，建立植樹模型。

【教學難點】

理解間隔數與棵數之間的規律并運用規律解決問題。

【教具準備】

課件、自主學習單、學具等。

【教學過程】

一、任務前置，以學定教

課前布置學習任務（學生獨立完成）：

“植樹問題”悅學單

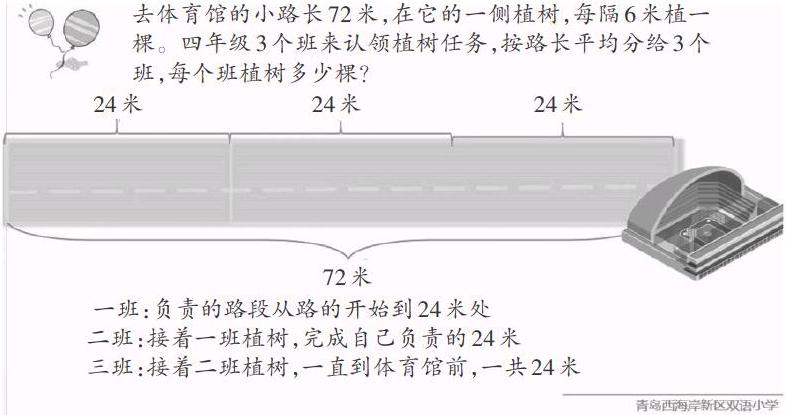
去體育館的小路長72米，在它的一側植樹，每隔6米植一棵。四年級有3個班認領植樹任務，按路長平均分給3個班來完成，每個班負責24米。

一班負責的路段從路的開始到24米處;

二班接著一班植樹，完成自己負責的24米;

三班接著二班植樹，一直到體育館前，一共24米。

每個班植樹多少棵？

【設計意圖：這個環節是由學生課前完成的，能夠給學生提供一個自主開放的空間，讓學生獨立思考問題，從而暴露學生的認知經驗和問題。教師就可以發現問題且充分把握學情，確定教學的重難點，體現以學定教。同時，這個情境把植樹問題的三種情況都包括在內，是實際生活中的真實情境，不是為了研究而研究，是基于問題解決來研究，有利于學生對知識的建構和理解?！皩W”在教之前，既實現了“先學后教”，也實現了“悅自主獨學”?！?/p>

二、小組合作，展示交流

師：昨天大家已經獨立研究了植樹問題，（板書課題：植樹問題）你們認為什么是植樹問題？

生1：有關植樹的問題就是植樹問題。

生2：研究樹與間隔的問題就是植樹問題。

……

師：那到底是不是你們想的這樣呢？今天就一起來研究。根據課件中的圖示，請在小組內交流自己的研究成果。

1.一班植樹棵數

（1）小組內交流自主學習的成果

師：可以用學具來試著擺一擺，說明一班植樹多少棵;也可以用一條線表示小路，用小線段或圓點表示樹，畫一畫，看看一班植樹多少棵。

（2） 班內展示小組研究成果

師：請匯報你們的研究成果。

生1：我們開始研究的成果是24÷6=4（棵），也就是看24里面有幾個6米，然后通過畫線段圖、擺小樹、交流、討論，發現一班植樹應該是5棵，24÷6=4（棵），4+1=5（棵）。（在黑板上畫出線段圖表示小路，點上圓點表示樹）

生2：我們組也認可這個結論，但是生1沒有說清楚為什么加上1棵，誰能講清楚？

生3：因為從頭到尾植樹的時候，最后還有一棵樹，也就是第一棵樹需要第一個空，第二棵樹需要第二個空，第三棵樹需要第三個空，第四棵樹需要第四個空，最后終點還有一棵樹，可是沒有空了，就把最后的這棵樹加上。

師：大家明白生3的講解嗎？數學上稱這個空為間隔。那24÷6 表示什么？4指的是什么？為什么+1？

生4：24÷6表示有幾個間隔，4是4個間隔，因為4棵樹對應4個間隔，最后一棵樹沒有對應的間隔，所以+1。

師：咱們一致得出結論，一班植樹5棵，這是兩端植樹的情況。因為一棵樹對應一個間隔，最后一棵樹沒有間隔相對應，所以要加上1，這里利用了一一對應的數學思想。（板書：兩端植樹 一一對應）

2.二班、三班植樹棵數

師：我們知道了一班植樹的棵數，那二班、三班植樹多少棵呢？在小組內繼續交流討論。

生5（在黑板上畫圖）：二班為24÷6=4（棵），因為二班的第一棵樹被一班植了，就不用植了，這樣一棵樹對應一個間隔，有4個間隔，所以植樹4棵。

生6：這道題也是利用了一一對應思想。

師：你聽得真仔細，還補充了數學思想，非常好。

師：一班是兩端植樹的情況，那二班是什么情況？

生（齊）：一端植樹。

師：對，是一端植樹的情況。那三班植樹多少棵？

生7：三班和二班一樣，第一棵樹被二班植了，就不用植了，這樣一棵樹對應一個間隔，有4個間隔，所以植樹4棵，列式為24÷6=4（棵）。

生8：我不同意你的說法，三班應該植樹3棵，因為最后是體育館，也不能植樹，末尾那棵樹不用植，所以是3棵，列式為24÷6-1=3（棵）。

（其他學生都表示同意）

生9：我覺得三班是兩端都不植的情況。

師：大家分析得很透徹，有理有據，不僅解決了二班和三班植樹棵數的問題，還推理得出二班和三班分別是一端植樹和兩端不植的情況。

（板書：一端植樹? ? 兩端不植）。

3.間隔數與棵數之間的關系

師：計算三個班的植樹棵數都有算式24÷6，都是先算出4個間隔，然后再+1，或不加不減，或-1，你們發現了什么？請在組內交流一下，然后匯報。

生10：兩端都植的情況，總有最后一棵樹沒有對應的間隔，所以“棵數=間隔數+1”;而一端植樹正好是每棵樹都對應一個間隔，所以“棵數=間隔數”;而兩端都不植的情況就是多了一個間隔，所以“棵數=間隔數-1”。

師：說得很好！發現了規律，表達有邏輯，還總結出了“通過兩端都植推理得出一端植樹和兩端都不植樹”的結論。

（板書：棵數=間隔數+1? ? ?棵數=間隔數? ? 棵數=間隔數-1 ）

【設計意圖：對于三個班植樹棵數的探究是在互動中完成的，教師給學生創設了寬松的環境，學生在自主獨立思考的基礎上，通過與組內成員充分交流、大膽發言、探究討論、暢談收獲、分析辯解，經歷了操作、分析、推理、驗證、解釋、歸納的過程，最后共同解決問題，建構植樹問題的模型。因為有和諧的師生關系作為基礎，學生樂于展示、樂于分享和上臺展示，在互動碰撞中實現對知識的認知、發現、頓悟和對自我的超越，學科素養在潛移默化中逐步提升。這樣的教學開啟了學生的口，活動了學生的手，也解放了學生的腦，體現了以學為主，真正起到了啟發學生智慧，引領學生學習，激發學生興趣，構建學科知識的作用，學生由“學會”慢慢向“會學”轉變，并逐漸“樂學”，真正實現了“和合作群學”。】

三、教師點撥，拓展提升

1.方法提升

師：根據我們總結的規律，可以解決類似的問題，如果只記得其中一種情況，另外兩種情況記不住了，怎么能很快知道另外兩種情況？

生11：可以通過一種情況推理得出后，只要+1、

+2，或-1、-2就能得出結論。

師：如果三個式子都記不住了，怎么解決呢？

生12：可以通過擺學具或畫圖的方式發現規律，再利用規律解決問題。

生13：5指4空，可以得到兩端都植的結論是“棵數=間隔數+1”;把大拇指去掉，4指4空，可以得到“棵數=間隔數”的結論;再把小手指握住，是3指4空，可以得到“棵數=間隔數-1”的情況。

師：真棒！我們完全可以借助身邊的學具和自己的手指，通過操作和探索發現規律，然后利用規律解決問題。這樣不僅掌握了知識，更主要的是學會了方法。

（板書：擺、畫、手）

2.建立模型

師：剛才我們解決了植樹的問題，知道有三種類型，生活中還有類似的現象嗎？

師（課件展示軍人列隊、學生做操站隊、公交站示意圖、衣服上的紐扣的圖片）：大家在這里能找到“樹”和“間隔”嗎？

生14：隊伍中的人相當于樹，兩個人之間的空相當于間隔;公交站牌相當于樹，兩站之間的距離相當于間隔。

生15：衣服上的紐扣相當于樹，兩個紐扣間的空相當于間隔，這是一端栽樹的情況。

師：大家說的都很到位，這些都是研究“樹”與“間隔”之間關系的一類問題，也就是點與線段之間的數量關系，稱為植樹問題。

【設計意圖：有效的教學活動是學生的學與教師的教的統一。教師要發揮主導作用，處理好講授和學生自主學習的關系。本環節在總結解決植樹問題的三種類型規律的基礎上，讓學生用數學的眼光觀察生活，找一找生活中類似植樹問題的現象，并思考可以把什么看作“樹”，引導學生感悟生活中“?！钡拇嬖?。學生在已有成果的基礎上，進一步提升、拓展，在學習掌握知識的基礎上總結方法、積累數學活動經驗，由“學會”向“會學”轉變，實現了“悅教師引學”，達成了深度學習?！?/p>

四、多元測評，展示成果

出示題目：

（1）四年級一班教室在4樓，每層樓有20級臺階，從1樓回教室需要走多少級臺階？

（2）體育館和圖書館之間相距60米，要在兩館之間的小路兩旁擺花盆，相鄰兩盆花之間的距離是3米，一共要擺多少盆花？

生16：第（1）題中，從1樓走到4樓要走3層臺階，也就是相當于有4棵樹、3個間隔，從而列出算式20×（4-1）=60（級）。

師：很好，找準了“樹”與“間隔”，并得出是兩端都植的情況，從而利用模型解決了問題。

生17：第（2）題是在兩館之間就是說兩端都不能擺花，兩旁就是要算出兩邊，所以得出（60÷3-1）×2=38（盆）。

【設計意圖：當堂檢測是教師了解學生對本節課知識掌握情況的一個重要手段，對教學效果的反饋有著非常重要的作用。在學生理解了植樹問題的三種類型后，再讓學生獨立解決一些數學問題，就能緊扣學習目標，強化學習重點，學生就能充分體驗學習的樂趣和獲得收獲的成就感，實現了“和評價促學”?！?/p>

五、拓展延伸，開放教學

師：這些圖中的植樹棵數與間隔數之間有什么關系？（動態演示，把封閉圖形轉化為直線）請課后繼續探究。

【設計意圖：學生的學習不止于教材，不止于課內，不止于教室內。這樣一個環節能幫助學生打開思維，拓展視野，這是開放的學習觀，這是一種大學習觀，這實現了“悅拓展延學”?！?/p>

六、回顧梳理，歸納總結

師：本節課首先是帶著學習任務，通過擺學具、畫圖、交流討論，得出植樹問題的三種情況，通過一一對應、數形結合，大家理解了棵數與間隔數的關系，發現了兩端植樹情況的規律是“棵數=間隔數+1”，并類比遷移得出一端植樹和兩端不植情況下的結論，建立了三個模型，并利用模型解決了問題。最后，把封閉圖形的植樹問題轉化為直線上的植樹問題，獲得了數學方法和思想。（動態出示思維導圖）

【設計意圖：通過回顧所學知識，學生獲得數學知識的同時，獲得了數學思想方法，提升了梳理、概括知識的能力。這樣能使學生在交流中鞏固新知，進一步體會數學與生活的密切聯系，真正實現了由雙基到四基，由兩能到四能的轉變，學生的數學素養悄然提升。】

【教學反思】

一、學為中心，以學定教

本節課采用“三環五步五學”的教學模式，凸顯“學為中心，以學定教”的生本理念，學生在自主學習的基礎上，與同伴共享自學資源，完整經歷了研究問題的全過程，學會了學習的方法，實現了由被動學習到主動學習的轉化，從而樂學、悅學。

二、追尋有思想的教學

日本教育學者米山國藏說過：“我研究了多年的數學教育，發現學生在初中、高中階段學習的數學知識離校后不到一兩年便很快忘光了，然而，無論他們從事什么工作，唯有深深銘刻于頭腦中的數學精神、數學思維方法、研究方法卻隨時發生作用，使他們受益終身。”顧沛教授指出：“數學思想是數學科學發生、發展的根本，也是數學課程教學的精髓。”依據課程標準的要求，我在這節課中力求凸顯數學思想的滲透，追尋有思想的教學。本節課重點突出以下三種思想：

1.一一對應思想

在植樹問題教學中，重要的是促進學生從本質上理解模型，因為無論哪種模型，其本質就是一一對應。

2.模型思想

讓學生操作學具、畫圖或用手指研究，自然建立植樹問題三種情況的直觀模型：加一、不加不減、減一。

列舉生活中的擺花、上樓梯等情況，將它們與樹的棵數和間隔數進行對比，也就是凸顯點與段數之間的對應關系，使學生感受到，雖然情境不同，但都是一類問題，凸顯數學模型。

植樹問題的模型是現實世界中一類相似事件的放大，它源于生活，卻高于生活。數學思想方法和數學知識相比，知識的有效性是短暫的，思想方法的有效性卻是長遠的，能夠使人受益終身。

3.數形結合思想

數與形反映了事物兩個方面的屬性。數形結合，主要指的是數與形之間的對應關系，把抽象的數學語言、數量關系與直觀的幾何圖形、位置關系結合起來，通過“以形助數”或“以數解形”，就能使抽象思維與形象思維相結合。

學生通過擺一擺、畫一畫，把植樹問題中棵數和間隔數之間的關系呈現得一目了然，從而使復雜問題簡單化，抽象問題具體化，這樣不但起到優化解題途徑的作用，也使數學思想方法得到滲透。

（責編 金 鈴）