運用“轉化思想”解析“組合圖形面積”問題小學六年級數學“組合圖形的面積”問題解析技法



摘要:解決組合圖形面積問題的關鍵,是需把組合圖形分解為一個個不規則的單體圖形,再根據每個單體圖形的形狀特點及其位置關系分析出隱含在這些單體圖形間的數量關系,再利用平移、旋轉、翻轉、割補、變形等轉化手段將這些單體圖形重新組合成新的基本圖形,使復雜問題簡單化。我們運用轉化思想在圖形的轉化上下功夫,就會讓解題思路新奇、解題方法巧妙。本文用例談的方式敘述了體現轉化思想的解析六年級較復雜的“組合圖形面積”的技巧:1割補法;2拆拼法;3變形法。
關鍵詞:轉化;割補;拆拼。
引言:組合圖形主要是指由圓形和一些基本圖形拼接或疊加后組合而成的新的圖形。轉化思想是一種重要的數學思想,所謂的轉化思想,就是把難轉化為易;把新的知識轉化為舊的知識;把陌生轉化為熟悉;把復雜轉化為簡單。
運用轉化思想,解析“組合圖形面積”問題,則是運用:分、合、轉、移、補、等變形手段將組合圖形轉化成簡單的圖形,或者是基本圖形。使復雜問題簡單化,以便找出新的解題思路,從而巧妙解答。
一 、割補法
割補法是圖形轉化方式的一種,即把組合圖形的一部分切割下來拼補到另一部分上去,把兩個不規范的單體圖形組合為一個基本圖形,或把復雜的圖形轉化成簡單圖形。再通過計算基本圖形的面積,得到陰影部分的面積。
割補法大體上有三種:平移法、旋轉法和翻轉法。即把切割下來的單體圖形,通過平移、旋轉、翻轉這三種方法把兩個單體圖形轉化成一個基本圖形,或有規律的組合圖形。
1:平移法
例題:如下面圖(1)所示,求陰影部分的面積。
分析:觀察轉化過程圖可知,從題圖中間處切割開,平移,把原組合圖形轉化成由正方形和圓兩個基本圖形組合而成的圖形。由轉化結果圖(3)得知:其陰影部分的面積的面積則為正方形的面積-內接圓的面積=陰影部分的面積。
答案:12×12-3.14×(12÷2)×(12÷2)=30.96平方厘米
2:旋轉法
例題:如下面圖(1)所示:四邊形ABCD是平行四邊形,圓的半徑是4cm 求陰影部分的面積。
分析:觀察組合圖形,連接AC,發現AB=AC,則陰影部分E與空白處F 的面積相等,如下圖:如果把陰影部分E切割下來,再通過旋轉、平移,拼補到空白處F處,則得到基圖形三角形ACD,新得到的三角形的底等于圓的直徑,三角形的高為圓的半徑,利用三角形面
積公式解答:
答案:S=ah=×4×2×4=16平方厘米
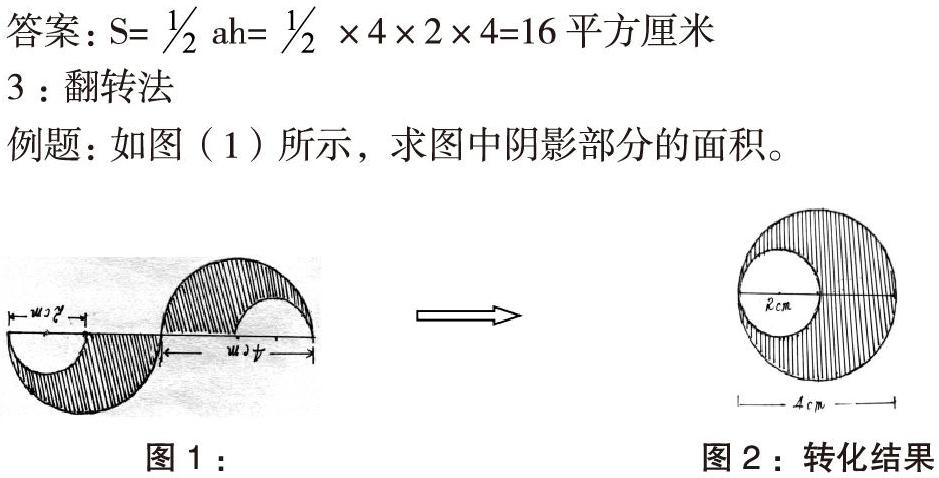
3:翻轉法
例題:如圖(1)所示,求圖中陰影部分的面積。
分析:看左圖(1)可知,此題如若繼沿用切割、旋轉、平移的方法轉化此題的話,則不能使此題簡化,須先切割,再翻轉最后再平移才能把復雜的組合圖形轉化成簡化圖形。
此題須沿直線切割,把圖形分解成上下兩部分,然后以直線的中點為支點把圖形的上半部分向左翻轉,使原圖轉化為一個偏心圓.如 轉化結果圖(2)
答案:(2×2-1×1)×3.14=9.42平方厘米
二、 拆拼法:
拆:就是分解圖形;拼:就是重新組合圖形。拆拼法即將疊加在一起的圖形分解開,成為一個個單體圖形,再把一個個單體圖形通過旋轉、平移等轉化方法,使其重新組合成一個有規律的組合圖形,使組合圖形各單體圖形間的數量關系顯現出來,以便解析起來更簡單明了。
例題:下面圖(1)中,等腰三角形的兩條直角邊長為4厘米,求陰影部分的面積。
分析:只看題圖,找不到突破口,無從下手,通過做輔助線,可以看出,題圖為兩個完全相同的半圓疊加在一起組成的,又因為等腰直角三角形的兩條邊相等且互相垂直,經過分解、旋轉、平移把題圖轉化為一個直徑為4厘米的圓,里面是最大的內接正方形。所以,陰影部分的面積=圓的面積-正方形面積。
答案:3.14×(4÷2)×(4÷2)-(4÷2)×(4÷2)÷2×4=4.56平方厘米
三 、變形法
變形拼補法是指將兩個不能拼補在一起的單體圖形中的一個,作變形處理,使其變成能拼補在一起的圖形。達到將復雜圖形轉化為簡單圖形的目的。但前提條件是變形前后圖形的面積不變。
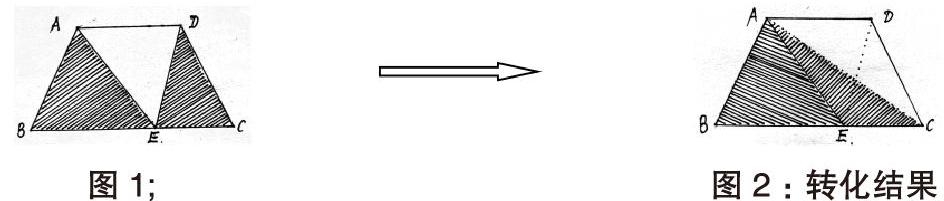
例題:如下面圖(1)所示,梯形ABCD 的下底為20cm高為10cm,求圖中陰影部分的面積。
分析:分析題意并結合看圖可知,求陰影部分的面積即求兩個三角形的面積之和,已知兩個三角形的高都是10厘米,不知道兩個三角形的底分別是多少。所以無法求得陰影部分的面積。如果我們改變一下思路,將已知條件轉化一下,看看是否可以。如右圖轉化結果所示。據定理:“等底等高的三角形,其面積一定相等。”將三角形DEC變形為等底等高的三角形AEC,問題則得到解決,所以三角形ABE的面積+三角形DEC的面積=三角形ABC的面積=陰影部分的面積。
答案:20×10÷2=100平方厘米
結束語:
上面介紹了三種解析較復雜的“組合圖形面積”的解析技巧,每一種解析技巧都貫穿著轉化的數學思想。轉化即變化;變化即靈活、即創新、即不墨守成規。靈活地運用知識,靈活地選用方法。把轉化的數學思想,運用于我們的數學實踐中。在潛移默化的過程中,讓靈活的思想、創新的思維,植根于學生的心中。
天津市寧河區苗莊鎮星光小學?天津 寧河區?張軍安

