通過一題多解提升學生的核心素養的方法探究
何歡歡

摘 要:時代的發展要求數學教師在教學中落實學生數學核心素養的培養,而習題講解是教學中的一個重要環節。文章從求解陰影圖形面積的習題入手,通過一題多解,引導學生深度思考,變式拓展,不僅可以加深學生對陰影部分圖形面積解法的理解和掌握,而且還有助于培養學生主動探究能力,從而達到提升數學學科的核心素養的效果。
關鍵詞:核心素養;陰影圖形面積;一題多解
當前,數學核心素養已成為數學教育界的熱門話題,史寧中教授說過:“數學學習的最終目標,是讓學習者學會用數學的眼光觀察現實世界,會用數學的思維思考現實世界,會用數學的語言表達現實世界。”我們能夠通過數學教育把學生培養成為什么樣的人,使學生具備哪些數學能力,這一直是我們一線教師要始終思考和落實的重要問題。每一位學生如何在數學課堂中獲得良好的數學教育,得到不同程度的發展,是我們每一位數學教師應該去深入探索研究的問題。因此,學生的數學核心素養的培養關鍵在于如何落實到平時的課堂教學中。
而數學的課后習題也是數學教學內容中一個重要的部分,所以教師同樣需要注重在習題課中落實數學核心素養的培養。習題課不是單純機械簡單的習題講評,它應該是一堂經過教師精心選材,合理設計,能夠引導學生進行深度思考,從而發展學生的數學思維,培養數學核心素養的課。文章嘗試結合一道課后求陰影圖形面積的習題的教學片段,來談談如何在一題多解教學中培養學生的數學核心素養。陰影圖形面積的求解方法靈活多樣,并且可能有多種不同的解法,通過一題多解,不僅可以加深學生對陰影部分圖形面積知識的理解和掌握,而且還有助于提升數學學科的核心素養。
一、 問題展示
習題來自新人教版九年級上冊第115頁第4題。
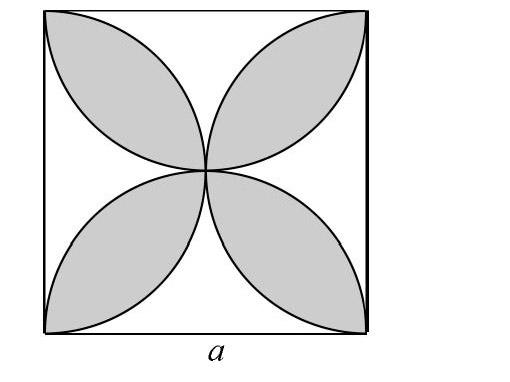
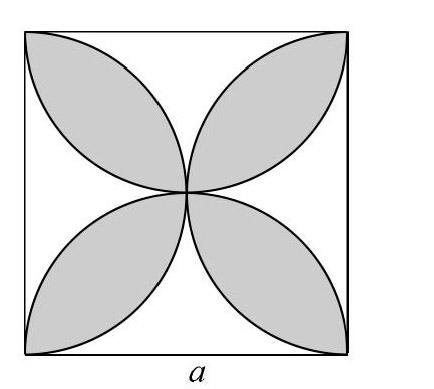
題目:如圖,正方形的邊長為a,以各邊為直徑在正方形內畫半圓,求圖中陰影部分的面積。
二、 教學分析
本題是《弧長和扇形面積》的配套習題。本題涉及正方形、圓以及三角形的面積等相關知識。解決這類題的關鍵是利用和差法將陰影部分的面積轉化為基本圖形的面積,要求學生具有較強的識圖能力和靈活變通的思維方式。而本題求解過程中所涉及的思想方法包含化歸、轉化、整體、數形結合、方程以及類比思想。
為了讓學生更好地解決問題,筆者在課堂中設置了鋪墊練習。
(環節一)鋪墊練習:
題目1. 如圖,以AB為直徑畫半圓,點C是弧AB的中點,求圖中陰影部分的面積。2. 已知正方形ABCD的邊長為a,以它的一組對邊為直徑向正方形內畫半圓,求圖中陰影部分的面積。3. 正方形AOBP的邊長為a,分別以點O、P為圓心,a為半徑向正方形內畫弧,求圖中陰影部分的面積。
陰影部分的面積表達式S陰影=??? S陰影=??? S陰影=
分析:以上三個圖形,第一個圖形是一個半圓內部有一個三角形,第二個圖形是一個正方形內部有兩個半圓,第三個圖形是一個正方形內部有兩個四分之一圓,且有重疊。求解第三個圖形面積的教學過程中,讓學生通過畫圖體會陰影部分形成的過程。
設計意圖:本環節三個題目遵循立足原題的原則,不僅讓學生復習陰影圖形面積的求法,還本著由淺入深、滲透方法、開啟思路的原則,使學生能夠從不同角度觀察、發現陰影部分與熟悉圖形之間的關系,為解決原題做鋪墊。心理研究的結果表明,由淺入深的順序更符合學生的認知發展規律。
有了鋪墊練習的引導,再讓學生來解決課本這道題。
(環節二)解決原題:
原題:如圖,正方形的邊長為a,以各邊為直徑在正方形內畫半圓,求圖中陰影部分的面積。(為方便敘述將原題陰影部分的每一片稱為“葉形”)
這個環節采取先給學生充分獨立思考的時間,教師可根據學生的情況給予適當引導,再讓學生分小組討論的方式來完成小結和反思,以便形成解題經驗。教師此時的角色轉化為傾聽者,將課堂放手給學生,讓學生去觀察,思考,發現問題,在討論中學習,激發學生對數學學習的興趣。此處讓學生從不同角度觀察陰影部分的構成。學生可能會想到先求出兩處空白部分的面積,再用正方形面積與空白部分面積求差,進而求陰影部分的面積。于是得到第一種解法。
解法1:先求出兩處空白部分面積,再用正方形面積減去空白面積的兩倍。
S兩個空白=S正方形-2S半圓=a2-πa22=a2-πa24
S陰影=S正方形-2S兩個空白=a2-2a2-πa24=πa22-a2
解法1中學生把注意力放在了兩個半圓上,緊接著筆者引導學生能否只利用其中一個半圓,找出它與葉形面積的關系。目的是讓他們把本題與鋪墊練習第1題聯系起來,想到將半圓分割成三角形和弓形,于是又有了第二種解法。
解法2:連接AO、BO,根據對稱性可知,一個“葉形”的面積=半圓面積-等腰三角形AOB的面積。
∴S陰影=4×(S半圓-S△AOB)=4×12πa22-12a·12a=4×πa28-14a2=πa22-a2
前兩種解法都是從靜態的角度來看陰影部分,我們也可以從動態的角度觀察。不妨讓學生通過畫圖來體會陰影部分的形成過程。有了這個體驗過程和鋪墊練習3的啟發,學生得到了如下解法。
解法3:因為陰影部分是四個半圓的重疊部分,所以:
S陰影=4×S半圓-S正方形=4×12πa22-a2=πa22-a2
在解決此類問題時,我們還可以考慮用代數的方法來解決幾何問題。為此,可以引導學生引進未知數,建立方程,用方程的思想解決幾何圖形求面積問題。
解法4:觀察發現該圖由若干個相同面積的部分組成,不妨設一個葉形面積為x,一塊空白部分的面積為y,則有

