融入數學文化　考查核心素養

覃淋　喻曉婷　張靜

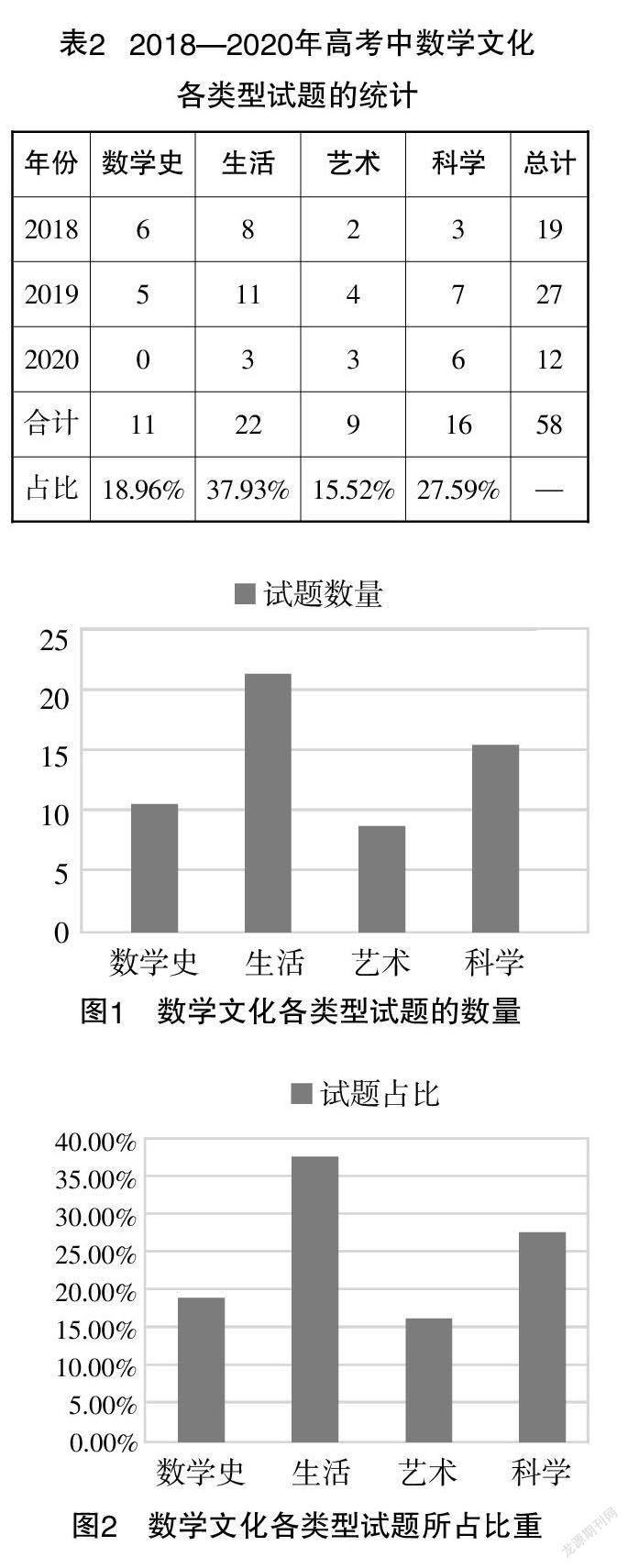
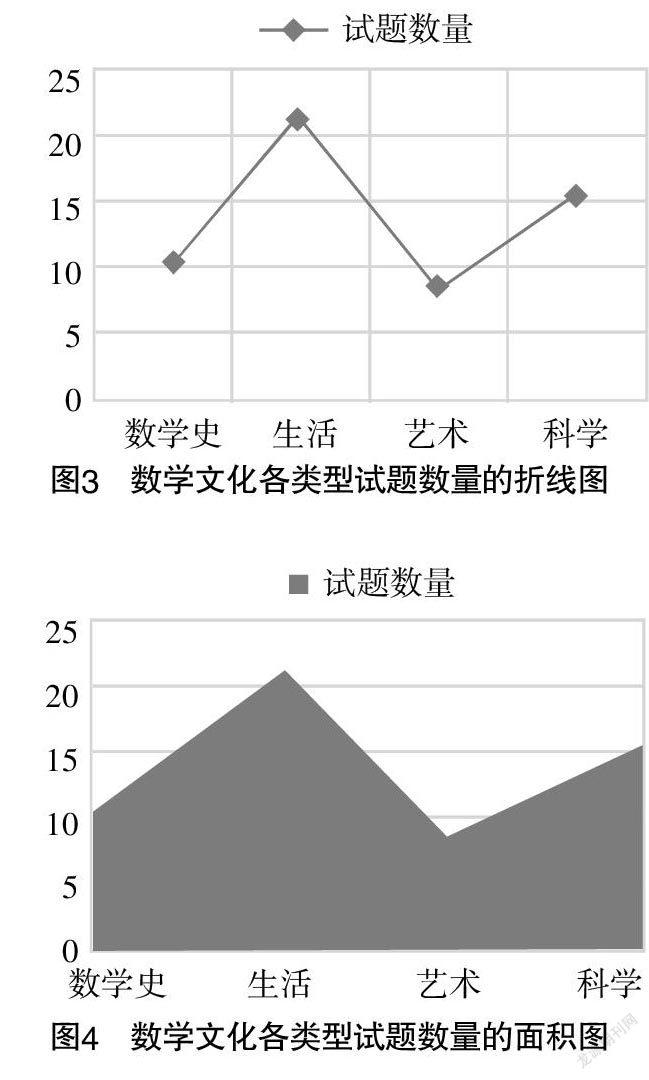
[摘? 要] 對2018—2020年高考數學全國卷中的數學文化試題進行統計分析，研究后發現：高考數學全國卷一直在積極探索如何將數學文化與高考數學試題相結合，將數學文化融入數學試題，考查數學學科核心素養. 高考數學全國卷將數學文化、數學試題與數學學科核心素養三者有機融合后進行考查，引導學生“會用數學的眼光觀察世界，會用數學的思維思考世界，會用數學的語言表達世界”.

[關鍵詞] 高考;全國卷;弘揚;數學文化;探索

引 言

“數學文化”一詞，是美國數學家懷爾德（R. L. Wilder）于1981年在《作為一種文化體系的數學》（Mathematics as a Culture System）中提出的，他從數學人類學的角度提出了“數學作為一種文化體系”的觀點. 這一觀點為研究數學的發展展現了一個新的視角，也為數學教育研究注入了新鮮的血液. 數學文化是提升學生數學核心素養的重要手段，具有非常重要的教育價值與文化價值. 從數學文化的角度來研究高考試題，是改進高中數學命題與教學改革的一個重要突破口.

《普通高中數學課程標準（2017年版2020年修訂）》（下文簡稱“新課標”）指出：要將數學文化融入數學教學活動中. 通過教學中滲透數學文化，讓學生了解數學的發展歷程，認識數學在科學技術和人類社會發展中所起的重要作用，引導學生認識和感悟數學的文化價值，樹立文化自信，提升人文素養和數學核心素養[1]. 2019年普通高等學校招生全國統一考試大綱（數學）在“個性品質要求”中提到：“要……