基于自編游戲情境的初中數學教學設計與反思
張佳萍


[摘? 要] “最短路徑問題”是各版本教材著力強調的重點,也是中考考查的熱點,筆者以自編游戲情境的形式演繹“最短路徑問題”,激發學生的內驅力,通過動手、動口、動腦培養學生的動手操作能力、合作互動能力與數學建模能力.
[關鍵詞] 自編;游戲情境;最短路徑;初中數學
“最短路徑問題”是各版本教材著力強調的重點,也是中考考查的熱點,其以“將軍飲馬”問題為經典模型,主要考查線段公理及軸對稱性質,常表現為求線段和的最小值. 教學中,教師雖著力分析與強調,但學生每遇此種類型題,總是一頭霧水,不知從何入手. 為了突破這個教學重難點,筆者以自編游戲情境的形式演繹“最短路徑問題”,激發學生的內驅力,通過動手操作、小組合作實現問題的突破.
基于游戲情境的教學設計
環節1? 經典永流傳.
“將軍飲馬”的故事:海倫是亞歷山大城里一位有名的學者. 有一天,一位將軍去拜訪海倫,想請海倫解答一個令這位將軍百思不得其解的問題:將軍每天從圖1中的營地A出發,到河流l(直線l)飲馬后再到營地B,那么將軍應在河流的什么地點飲馬,所走的路程才能最短呢?[1]
設計意圖? 首先介紹“將軍飲馬問題”的出處,給學生以歷史的真實感,以著名學者海倫解決“最短路徑問題”引起學生重視,激起學生的學習欲望和學習興趣.
環節2? 自編游戲情境——悟空降妖除魔.
科學家愛因斯坦曾言:“興趣是最好的老師.”一個人只有對一件事產生了興趣,才會自主去探究與發現,且在探索求知的過程中,他的情緒是愉悅的,學習的效果也是最佳的.
游戲背景:話說唐僧師徒四人去西天取經,一路上披荊斬棘,降妖除魔,為了取得真經可以說歷盡艱險,上演了一段段英雄傳奇的故事.
設計意圖? 通過學生耳熟能詳的《西游記》讓其在感受中華傳統文化的同時,自然進入本節課學習的重難點,把本節課的各類問題置于闖關游戲中,游戲關卡由淺入深,不斷遞進.
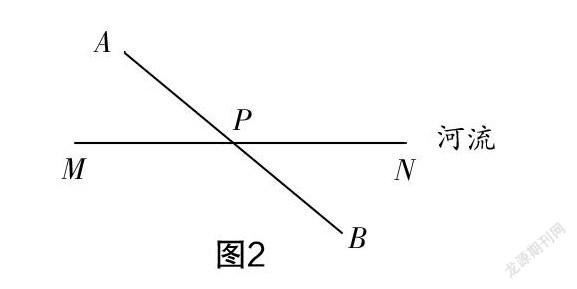
第一關:唐僧師徒四人來到黃風嶺,在河流的下游A處休息時下起了暴雨,河水漲得很快,他們應盡快到對岸河流上游的B地才能躲避險情,走怎樣的路線才能最節省時間呢?(最短路線的設計如圖2所示)
設計意圖? 此類問題是“最短路徑問題”中最簡單的一類,只需應用線段公理“兩點之間,線段最短”就可以解決問題. 學生由此經歷了從實際問題到數學問題的一小步,為下面繼續闖關提供了理論支撐.
第二關:唐僧師徒四人到五莊觀投宿,豬八戒引誘孫悟空去偷來人參果,師兄弟一起分享. 道童發現人參果少了幾個,怒罵唐僧師徒四人,孫悟空怒不可遏,把人參果樹推倒. 趁著夜色師徒四人匆匆逃逸,鎮元大仙用法術將他們捉了回去. 鎮元大仙聲稱,如果孫悟空能夠解決“將軍飲馬問題”,就放他們師徒四人走.
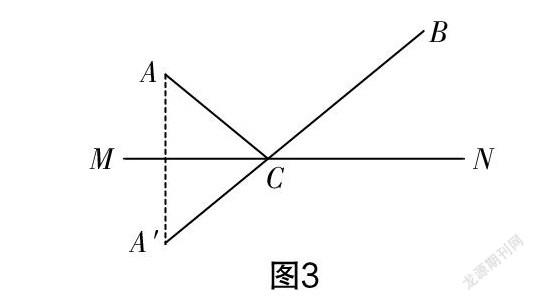
設計意圖? 讓經典故事在第二關中重現,一方面是學生必須解決這個經典問題才能解決其他問題,另一方面是突出本節課的重點——引導學生如何將實際問題轉化為數學問題,強化學生的轉化能力. 學生幫助孫悟空從中抽象出的數學模型如下:在固定直線MN的同側有兩個固定點A,B,在直線MN上求作一點C,使AC+BC最小. 解決方法為:作點A的對稱點A′,連接A′B與直線MN的交點C就是所求作的點. 如圖3所示.
第三關:唐僧無意中闖進了黃袍怪的洞府. 黃袍怪的夫人原是寶象國公主百花羞,十三年前被擄進波月洞. 她悄悄放走了唐僧,請他給父王送信. 為了讓父王相信師徒四人,百花羞把“將馬飲馬問題”的證明過程交給了師徒四人,作為他們見面時的信物:
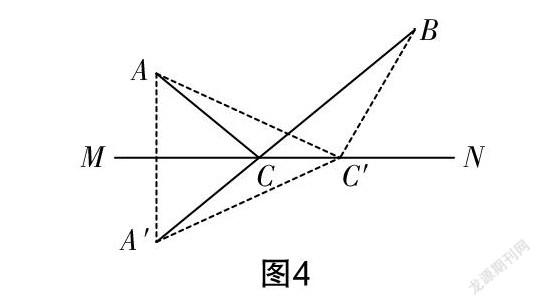
如圖4所示,在直線MN上取一點不同于點C的點C′,分別連接AC′,BC′,A′C′. 由軸對稱的性質,得AC=A′C,AC′=A′C′,這樣AC+BC轉化為A′C+BC,即轉化為A′B,且AC′+BC′轉化為A′C′+BC′. 因為在△A′C′B中,根據三角形的三邊關系,得A′B< A′C′+BC′,所以AC+BC最小.
設計意圖? 學生掌握數學模型僅是“知其然”,還應“知其所以然”. 通過證明這種作圖方法的正確性,才能讓學生信服,從而進一步理解這種作圖方法的深層含義,即利用軸對稱的性質用點A的對稱點將其代替,從而實現“化折為直”的目的.
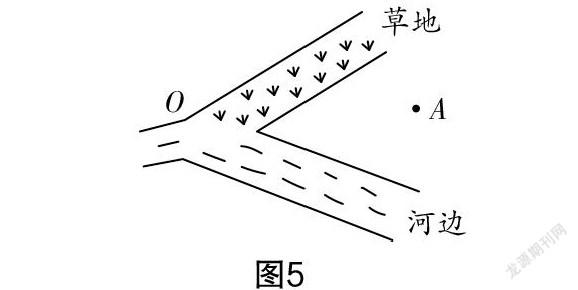
第四關:祭賽國金光寺幾年前一陣血雨過后,寺中塔頂的舍利子佛寶無影無蹤. 僧人們被罰受苦,沉冤難雪. 為查失寶,悟空攜八戒入碧波潭,先禮后兵,與龍王之女乃圣公主及九頭蟲駙馬交戰. 白龍馬化做少年,入潭尋見乃圣公主,設計騙回佛寶. 如圖5所示,為了犒勞白龍馬,決定讓白龍馬從A地出發到草地吃草,再到河邊飲水,最后再回到點A,白龍馬如何走路徑最短?
作圖過程如圖6所示,分別作點A關于直線OM,ON的對稱點A′,A″,連接A′A″,與OM,ON的交點(點B,C)就是所求作的點.
設計意圖? 解決第四關游戲問題是知識的再遷移:第三關游戲問題作一次軸對稱即可解決,而第四關游戲問題則需要作兩次軸對稱才可以解決. 實際上解決的是在角的內部作一個周長最小的三角形的問題,開闊了學生的視野,提升了學生的思維水平.
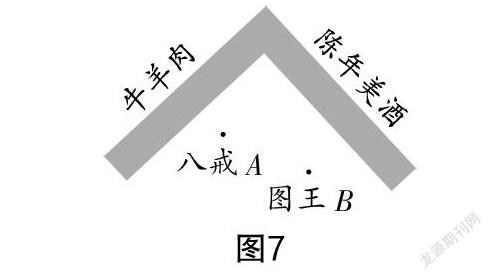
第五關:玉華州國王下旨逐僧出境. 唐僧師徒四人來到州境,適逢三個太子領兵盤查,四人分別躲進米缸、衣箱、席筒、木柜內,被抬進宮去聽候發落. 夜間,悟空用隱身術潛入宮中,作法把國王、王后、妃嬪等滿朝文武頂上頭發全部剃光. 國王很受教訓,懺悔排佛不對,禮遇唐僧師徒. 為感謝師徒四人對自己的成功勸諫,設宴款待師徒四人. 如圖7所示,宴席上,在A處的八戒準備先去取一塊牛肉,再去取一壇美酒,向國王敬上一杯酒后回到自己的位置,八戒如何走路徑最短?
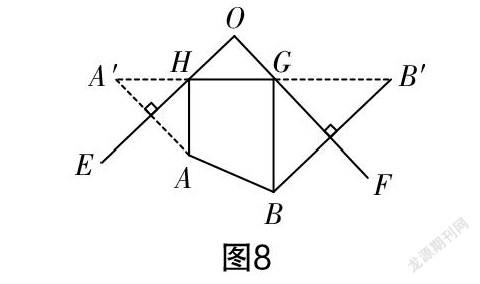
作圖過程如圖8所示,作點A關于OE的對稱點A′,作點B關于OF的對稱點B′,連接A′B′,與OE,OF的交點(點H,G)就是所求作的點.
設計意圖? 第五關游戲問題雖然也是通過作軸對稱解決的,但與第四關游戲問題不同的是,這里在一個角的內部有兩個固定點,實際上解決的是在角的內部求作一個周長最小的四邊形的問題. 通過以上問題的解決,學生能夠明白:解決“最短路徑問題”就是解決“軸對稱問題”,其關鍵是找準固定點和固定直線,繼而作出對稱點.
基于游戲情境的教學反思
本節課的設計主線是“實際生活問題—數學知識問題—解決數學問題—解決生活問題”[2]. 在數學課堂教學中,筆者先通過數學建模引導學生把生活問題轉化為數學問題,接著用數學知識解決數學問題,最后運用數學問題的結論去審視生活問題,從而有效提高學生的應用意識.
教學設計中,教師要學會處理和加工教材,創設出學生易于接受的形式多樣的教學情境,才能突出重點、突破難點[3]. 本節課通過《西游記》的故事讓學生感受中華傳統文化的同時,學會如何解決“最短路徑問題”,體現了由簡單到復雜、由淺入深的教學進程.
本節課以學生自主探索為主,采用了情境教學與任務驅動法,在教學過程中,輔以學習小組的合作互動,通過動手、動口、動腦,鍛煉學生的動手操作能力、合作互動能力與數學建模能力.
參考文獻:
[1]丁力. 初中數學幾何最值問題探究——以“將軍飲馬”問題模型的解題策略為例[J]. 數學教學通訊,2020(14):79-80.
[2]杜慶術. 數學游戲在初中數學教學中的應用[J]. 中學數學,2019(22):92-93.
[3]張偉俊. “綜合與實踐”課的教學探索與實施建議——以“探究最短路徑問題”為例[J]. 中國數學教育,2015(11):11-14.

