聚焦核心素養 突出運算能力

岳劍平

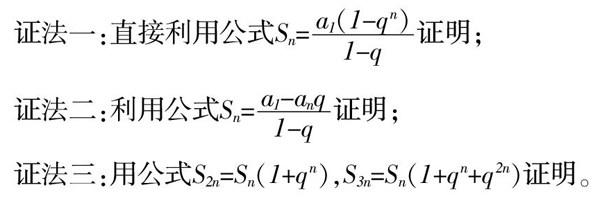
摘? 要：運算能力是學生學習數學應該具備的關鍵能力，也是數學核心素養的重要內容，培養學生運算能力既是新課改對廣大數學教師提出的根本要求，也是學生發展的內在需要。本文以高中數學教學為例，聚焦數學核心素養要求，簡要分析當前高中學生數學運算存在的一般問題，重點探討高中數學教學中如何著重培養學生數學運算能力，為促進學生數學核心素養發展奠定基礎。

關鍵詞：高中教育;數學教學;核心素養;運算能力

一、數學運算的一般問題

運算能力不是指簡單地計算，其核心是“運算”，主要包括運算對象和運算規律兩方面內容，從小學到高中，學生面對的數學運算對象和運算規律越來越復雜，需要解決的運算類問題也越來越多，尤其是到了高中階段，學生不僅需要運用數學知識解題，更需要具備良好的運算能力才能確保問題正確快速得以解決。從當前高中學生運算相關問題的學習現狀來看，大部分學生存在如下幾方面問題：

一是審題不完善。從教學實踐來看，很多學生從小學到高中，始終存在審題問題，審題不全面，對題干信息的挖掘比較片面，很難快速挖掘出題干的隱含信息，導致運算難度變大，運算不正確，最終影響解題效率和正確率。

二是基礎不扎實。是否能夠正確運算是基于學生是否真正理解和掌握數學基礎知識的，只有掌握數學概念、定理、公式、法則等基礎知識，才能靈活地、正確地運用這些數學基礎知識和數學規律解決實際問題。但事實卻是很多學生將這些基礎知識背到滾瓜爛熟了，即使是將數學概念、定理、公式牢記于心，但也會出現運算失誤，根本原因在于學生對內涵和外延理解不清，對數學公式、定理、發展理解不透徹，容易擴大或者縮小基礎知識應用范圍，導致運算錯誤。

三是運算思維不靈活。運算不僅是計算過程，也是學生對條件、問題進行分類討論、歸納整理的過程，很多學生在運算過程中總是存在討論不全面，分類不嚴謹，影響了運算效率和正確率。

四是策略選擇失誤。數學運算過程其實也是學生選擇解題策略能力的直接體現，選擇合適的解題策略，運算效率也會事半功倍，選擇錯誤的解題策略，運算量和難度可能都會加倍。不少高中學生仍然無法正確結合問題選擇合適的解題策略，比如某一問題應該運算數形結合思想還是類比推理，判斷錯誤導致策略選擇錯誤，最終影響運算結果。

二、聚焦核心素養，培養學生運算能力的策略

（一）重視過程教學，夯實基礎知識

基礎是關鍵，基礎知識掌握是否扎實，理解是否透徹，都直接影響學生運算效率，制約學生運算能力提升。新高考大綱也對學生運算能力做出了明確界定，強調運算能力包括學生對運算條件、方向的選擇能力以及運算公式應用能力和計算方面的能力。為此，在教學實踐中，數學教師應重視數學概念、公式、定理、法則等基礎知識教學，摒棄傳統的死記硬背教學方式，引導學生自主歸納概念、推導公式、總結定理和法則，讓學生成為學習的主人，真正經歷知識形成過程，更透徹和全面地理解掌握這些基礎知識，為學生靈活運用基礎知識解決實際問題奠定基礎。

在指導學生解不等式（x+2）（3-2x）>0時，就可以先從算理著手，引導學生分析算式-2x2-x+6>O和（x+2）（3-2x）>0之間的關系，讓學生明白（x+2）（3-2x）>0是由-2x2-x+6>0這一算式分解而來的，由此可以發現算式是一條開口向下的拋物線，不等式的解集應該處于兩解之間，再結合圖形相關知識，將原不等式中的3-2x改寫成-（2x-3）即可快速破題。這一過程其實就是算理的運用過程，既深化了學生對算理的理解，也提高了學生解題效率，有效避免了學生運算錯誤。

（二）剖析經典例題，總結運算規律

當學生掌握了基礎知識并且對知識形成一定的體系后，教師還需要引導學生總結數學運算規律。因為基礎知識能夠有助于學生理清解題思路，但學生還無法敏銳地、靈活地解決問題。其原因就是學生對運算規律掌握不全面。鑒于此，不妨適當給學生增設經典例題，師生共同剖析經典例題，在例題磨合中總結規律，讓學生真正做到具體問題具體分析，在例題中分析和琢磨運算條件、探究解題方向，總結運算規律。經過長期訓練，學生掌握的運算規律更全面，在運算過程中更能靈活應對。

例如：函數f（x）=1/ln（x+1）+4-x2的定義域為（ ）

A. [-2，0]∪（0，2） B. （-1，0）∪（0，2）

C. [-2，2] D. （-1，2）

此題中，函數存在的意義是x+1>0且ln（x+1）≠0，同 時，4-x2≥0，換言之即是：x>-1且x≠0-2≤x≤2即-1

（三）巧設一題多解，培養學生多變運算思維

思維是影響能力的關鍵因素，良好的運算思維是高中學生學好數學這門課程應該具備的，也是提高學生運算能力的核心。在核心素養指導下，廣大數學教師已經充分意識到學生思維培養的重要性，而以突出運算能力為主的數學教學也必須加強學生運算思維培養。針對此要求，建議廣大數學教師適當給學生增設一些一題多解類習題，通過一題多解對比分析，促進學生對運算法則的理解，也間接培養學生概括能力、分析能力、歸納能力、解題能力，促使學生思維向多變性、靈活性、開放性、創新性發展。如下列例題，教師可重點引導學生探究多種解題方法，并且鼓勵學生從眾多解題方法中歸納總結最簡單、效率最高，最適合自己的方法。

例題1：解不等式3<2x-3<5，此題就有多種解法。

解法一：結合絕對值定義分類討論求解;

解法二：將原不等式轉化為不等式組求解;;

解法三：利用等價命題法解題;;

解法四：利用絕對值的集合意義解題。

例題2：已知等比數列Sn的前n項和，S3，S6，S9成等差數列，求證：a2，a5，a8成等差數列。

證法一：直接利用公式Sn=證明;

證法二：利用公式Sn=證明;

證法三：用公式S2n=Sn（1+qn），S3n=Sn（1+qn+q2n）證明。

事實證明，定期給學生設置一些一題多解類例題，引導學生從一題中探索多種方法，從多種方法中總結最佳方法，不僅是對學生進行專項實戰訓練，更是對學生進行運算思維訓練，潛移默化地培養了學生多變思維，提高了學生運算能力。

三、結語

隨著課程改革的深入，核心素養已經成為指導廣大數學教師開展教學活動的理論思想，以核心素養為導向的高中數學教學首先要重視學生運算能力培養，不斷創新教學方法，優化教學過程，以提高學生運算能力，為學生數學核心素養發展夯基。

參考文獻：

[1] 邱光云. 基于核心素養下高中數學運算能力培養的策略研究[J]. 讀寫算，2019（22）：120-121.

[2] 謝永清. 高中生“數學運算”素養的落地之策[J]. 當代教育與文化，2018，10（03）：81-84.

[3] 蔡述鈴. 基于數學運算素養的高中數學教學模式探究[J]. 高考，2020（18）：166.

（責任編輯：莫唯然）

本論文系福建省教育科學“十四五”規劃2021年度課題“高中數學學生閱讀理解能力的教學研究”（課題立項批準號：FJJKZX21-020）研究成果。