胸中有丘壑，方能繪山河

劉世雄

【摘要】本文基于整體性和結構化的觀念，以“二次根式”的教學為例，提出整體性教學應注重知識間的前后貫連，以舊引新；強調結構化教學應注重新舊圖式體系的相互作用；整體性結構化教學應體現連貫的思想、形成普適方法，學會用相似的方法做不同的事情，感受類比中所蘊含的數學基本思想、數學基本活動經驗的力量.

【關鍵詞】初中數學；二次根式；類比

傳統數學教學推崇“堂堂清”，針對每節課的知識點，推崇大容量、快節奏，以期達到當堂鞏固的效果.這往往造成教學過程推進過快，知識的生成著墨不夠，學生難以形成整體性的知識結構.如果教師沉迷于一個接一個的知識點教學，局限在一招一式的雕蟲小技，長此以往容易迷失在局部，無法形成系統性思維，最終必將導致只見樹木不見森林的后果，學生的整體性大局觀的形成便成了無源之水無根之木.

《義務教育數學課程標準（2022版）》在教學建議中指出，“在教學中要重視對教學內容的整體分析，建立對未來學習有支撐意義的結構化的數學知識體系”.由此可見，新課程改革注重整體把握教學內容，倡導結構化教學.這不僅要求貫通新舊知識之間的內在關系，還要求建立聯系通暢的結構化認知系統.正如章建躍博士所言：數學教學要以“研究一個數學對象的基本套路”為指導，設計出體現數學的整體性、邏輯的連貫性、思維的系統性的系列化數學活動.在類比中加強數學知識的整體架構，在類比中應用一般觀念的統攝指引，以實現從“知其然”到“知其所以然”再到“何由以知其所以然”的跨越.

為說明上述基本想法，下面筆者結合近期所聽到的一堂章起始課“二次根式”談起.

1 教學過程概要與觀課思考

環節一 創設情境 概念形成

問題1 教材“思考”題：

請嘗試用含有根號的式子填空：

（1）2的算術平方根為____.

（2）若正方形的面積為3，則它的邊長為____；

若正方形的面積為S，則它的邊長為____.

（3）若矩形的面積為195，且長是寬的3倍，則它的寬為____；

若矩形的面積為S，且長是寬的3倍，那么它的寬為____.

學生思考后回答：（1） /2.（2） /3； /S.

（3） √65； √S/3.

問題 上面問題中，觀察上述問題的結果.

（1）這些數與式分別表示什么意義？

（2）從形式上看都有什么共同特征？

思考歸納.

例1 當x 取何值時，下列根式有意義？

（1）√（x－2）；

（2）√（-2x+1）.

觀課思考 環節一完整地展示了概念教學過程中的概念形成過程，從熟悉的面積情境出發引入課題，借助學生已有的算術平方根學習經歷，既合乎知識間的邏輯連貫，又符合學生的認知結構；緊接著引導學生觀察所給數與式，發現共同特征，歸納定義.

人教版初中數學教材從數到式的教學編排貫穿始終，因此開篇直接表明從數到式，體現類比的學習模式，類比分數研究分式，再次實現從一類數到一類式的跨越.故而在章起始課中，我們首先要通過類比發現研究對象.從算術平方根出發，回顧其相關知識，再通過板書算術平方根的定義來構建它與二次根式的本質聯系.

環節二 互助合作 探究性質

思考 如何理解二次根式√a （a≥0）的雙重非負性？為什么？

探究1 當a≥0時，“a2”化簡的結果是怎樣的？

觀課思考 眾所周知，代數性質運算中的不變性就是代數的基本性質，其基本方法是“算算看”.所以探究1和探究2均采用填空，讓學生經歷計算、觀察、猜想、再利用不完全歸納法歸納出二次根式的性質.課堂實踐中，教師引導學生自主探究，既注意培養學生觀察能力，也注重提升歸納概括能力.

但是環節二性質的探究出現比較突兀，銜接不夠自然，學生不僅不明白學習二次根式的性質的必要性，更談不上理解與后續內容的邏輯關系.環節一通過類比獲得了研究對象——二次根式；環節二應順應這種類比，從已有分數到分式的學習經歷，對本章學習做一個“全景式”的展望，建立起本章知識的整體架構.讓學生自己可以想到將要學習的內容，讓學生明白所學內容前后的邏輯關系，從而實現從“知其然”到“知其所以然”再到“何由以知其所以然”的跨越.

環節三 反思提升 實現生長

問題 談一談你對二次根式定義的理解.說一說這節課涉及哪些數學思想方法？

觀課思考 反思提升通過“談一談、說一說”，回顧本節課學習的概念和性質，總結知識獲得和技能形成，積累基本活動經驗，感受數學思想方法.

2 教學再設計

環節一 從數到式

請嘗試用含有根號的式子填空：

（1）若正方形的面積為3，則它的邊長為；

若矩形的面積為195，且長是寬的3倍，則它的寬為___.

（2）若正方形的面積為S，那么它的邊長為___；

若矩形的面積為S，且長是寬的3倍，則它的寬為____.

追問：（1）中表示的數√3和√65表示什么意義？

（2）中的式子與（1）中的數有怎樣的關系？它們有什么共同特征？

設計意圖 直接開篇明義，點明主題從數到式.例題設置再次順應主題，結合算術平方根的定義，明白知識間的本質聯系.由此因勢利導得出類比要解決的第一個問題——發現研究對象，二次根式的出現水到渠成.

環節二 全景展望

問題1 事實上，式的學習的基本思路、內容和方法是一致的，你可以概括研究分式的基本思路、內容和方法嗎？

問題2 類似地，你認為我們應該如何展開二次根式的研究呢？

設計意圖 研究二次根式的基本思路、內容和方法與分式的研究是一致的，只需要把研究對象從分式變成二次根式.所以二次根式的學習要充分發揮分式的已有學習經驗，從總結分式學習開始.為此可以采取“先行組織者”的教學策略，以問題串引導學生展開探究從而實現類比要解決的第二個問題——建立本章知識的整體架構.

問題3 我們知道分式的性質就是分式運算中的不變性規律，類似地，二次根式的性質就應該從具體的運算入手，通過算一算再發現其不變性規律.

設計意圖 在整體框架下，一般觀念的指引下，研究的方向清晰，研究的內容明確，在相同的研究方法指引下，不僅大大降低學習的盲目性，而且有力加強學習的主動性，學生自主發現問題和提出問題便有了可能.

環節三 回顧提升

問題4 可以概括下這節課我們是如何學習的？

設計意圖 結合本節課的研究歷程，引導學生形成從數到式的研究的基本套路，將內隱的思維顯性化.正如章建躍博士強調的“研究對象在變，研究套路不變，思想方法不變.在整體性教學框架下，通過類比展現數學基本思想、數學基本活動經驗的力量！”

3 基于整體性和結構化的數與式的教學再思考

（1）整體性結構化教學應注重知識間的前后貫連，強調以舊引新.

數學整體性教學是注重新知和舊知的前后貫連，學生的認知必須建立在已有的學習經驗上，通過以舊引新促進新的認知結構的形成.

數與式經歷了整數到整式，分數到分式后，二次根式是從算式思維到代數思維的又一次飛躍.二次根式與實數中算術平方根緊密聯系，是非負數的算術平方根概念的進一步的抽象表示.它是特殊的含有根號的數到一般地含有根號的式.所以教學中一定要加強知識間的縱向聯系，知道從哪里來？將要學習什么內容？比較中體會知識間的前后貫連，以舊引新.

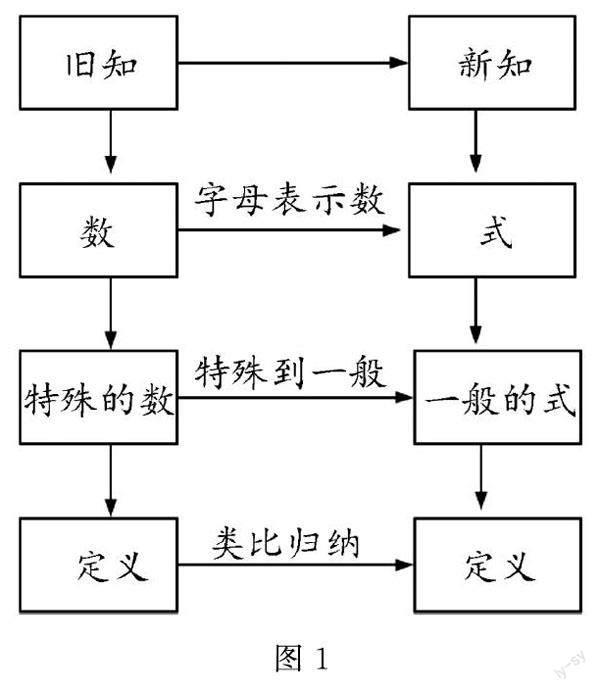
皮亞杰在《結構主義》提出結構就是圖式體系的論斷，認為新知學習是新、舊圖式體系相互作用的過程.因此在新知的教學中，要把零碎的知識有效結成網、組成圖式體系，形成知識的模塊化.由此可見，在上述教學環節一中可以用圖式體系（圖1）回顧算術平方根的相關知識，讓“舊知”可視化，圖式直觀化，悄無聲息地將學過的知識融入新的認知結構，以舊引新.這種圖式體系好似一張“聯絡圖”，讓老師有線索地教，學生有方向地學.

（2）整體性結構化教學應體現連貫的思想、形成普適方法

隨著《義務教育數學課程標準（2022版）》的頒布，基于核心素養的單元教學設計成為當下新課程改革的熱點，倡導以核心素養為導向做好單元教學的整體規劃.由此可見，與大單元教學呼應的是整體性教學.其目的是讓學生在整體的學習中，建立起適合的認知結構，形成數學學習的普適方法、基本套路.正如章建躍博士提出的代數研究的一般方法按照“引入——定義、表示、分類——性質——運算與運算律”一以貫之.正是因為研究對象相同，研究主題聚焦，研究的思路與數學思想一致，容易形成普適方法，獲得基本套路.

項武義教授《基礎代數學》中指出“引入一種新的數（或式），就要研究它的運算……”，由于二次根式對非負實數進行開平方運算得到，因此接著的研究主題自然就是二次根式的運算，而對代數運算進行化簡則是運算的本質，其化簡的依據就是性質.由此可以看出，性質可以保證運算結果的簡約屬性.這就明白為什么會在進行二次根式運算之前要學習二次根式的性質.當然在實際教學中可以充分發揮“分式的先行組織者”的示范作用，先概括分式的研究歷程、線索和基本方法，以流程圖的圖式體系呈現（圖2），以期學生對將要學習的內容，研究的方法有一個清晰的方向.認清學習二次根式內容的大方向，厘清知識間的前后邏輯，學會用基本套路實現整體架構.

這種“全景式”的認識和把握，不僅可以明白知識的產生以及背后的邏輯；還可以將思想方法和活動經驗等隱性知識轉化為顯性知識，讓學生學會學習；這種用相似的方法做不同的事情一般方法，思想連貫、方法普適，極具遷移性.整體性結構化教學讓教學主線連貫；研究對象統一，研究思想一致；整體系統規劃、教學目標協同，可高瞻遠矚的教，亦能胸有成竹的學，好似胸中有丘壑，輕松繪出數學壯美的山河.

參考文獻：

[1]中華人民共和國教育部制定.義務教育數學課程標準（2022年版）［M］.北京：北京師范大學出版社，2022.

[2]章建躍.章建躍數學教育隨想錄[M]杭州：浙江教育出版社，2017.

[3]項武義.基礎代數學[M].北京：人民教育出版社，2011.

[4]劉乃志.“整體數學”教學研究與實踐探索[M].北京：中國國際廣播出版社，2021.

[5]邢成云.統整初中數學課程：站在課程高度教學[J].中小學課堂教學研究，2021（05）：9-12.