核心素養(yǎng)視角下初中數(shù)學(xué)章統(tǒng)領(lǐng)課的實踐與反思

高凱亮 周沁

［摘? 要］ 如何在常規(guī)教學(xué)中提升學(xué)生核心素養(yǎng)是當(dāng)下熱議話題，學(xué)者們在實踐研究中發(fā)現(xiàn)，章統(tǒng)領(lǐng)課是提升學(xué)生核心素養(yǎng)的有效途徑之一. 文章對蘇科版“一元二次方程”章統(tǒng)領(lǐng)課的價值進行分析，幫助學(xué)生構(gòu)建“一元二次方程”章學(xué)習(xí)框架時形成策略性知識，并對章統(tǒng)領(lǐng)課的作業(yè)設(shè)計與評價進行反思，助力提升學(xué)生核心素養(yǎng).

［關(guān)鍵詞］ 核心素養(yǎng)；章統(tǒng)領(lǐng)課；一元二次方程

基金項目：本文是2021年度貴州省六盤水市六枝特區(qū)基礎(chǔ)教育教學(xué)課題“雙減背景下基于數(shù)學(xué)核心素養(yǎng)的單元教學(xué)設(shè)計研究——以方程、不等式為例”的階段性研究成果，該課題由第一作者與第二作者聯(lián)盟合作研究.

作者簡介：高凱亮（1995—），本科學(xué)歷，中學(xué)二級教師，從事初中數(shù)學(xué)教學(xué)與研究工作，南京市浦口區(qū)杜育林名師工作室核心成員，南京市江北新區(qū)第三屆初中數(shù)學(xué)工作坊核心成員，曾獲南京市江北新區(qū)第三屆“教育科研成果創(chuàng)新獎”特等獎.

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》指出，教師要選擇能引發(fā)學(xué)生思考的教學(xué)方式，重視章統(tǒng)領(lǐng)整體教學(xué)設(shè)計，改變過于注重以課時為單位的教學(xué)設(shè)計，體現(xiàn)數(shù)學(xué)知識之間的內(nèi)在邏輯關(guān)系［1］. 章統(tǒng)領(lǐng)課是本章的起始課（種子課），它不同于新授課，課堂上教師不僅要讓學(xué)生關(guān)注本章“學(xué)什么”，更要讓他們關(guān)注“為什么學(xué)，怎么學(xué)”，要培養(yǎng)學(xué)生有“飲水思源”的意識，并在構(gòu)建本章知識框架的過程中形成策略性知識，讓學(xué)生感受知識發(fā)展的連續(xù)性、必然性與合理性，從而潛移默化地提升學(xué)生的核心素養(yǎng).

基于學(xué)習(xí)價值的教學(xué)分析

筆者對蘇科版“一元二次方程”章統(tǒng)領(lǐng)課的學(xué)習(xí)價值進行分析，認(rèn)為其價值主要體現(xiàn)在下面兩個方面.

1. 感悟知識的整體性與必然性，樹立整體觀念

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》指出，要從整體上把握教學(xué)內(nèi)容，注重教學(xué)內(nèi)容的結(jié)構(gòu)化［1］. 學(xué)生在七年級學(xué)習(xí)過一元一次方程、二元一次方程（組）、三元一次方程（組），甚至類推到n元一次方程（組）. 七年級是將一元一次方程在“元”上進行推廣，這便為九年級將一元一次方程在“次”上進行推廣的合理性埋下伏筆. 對于一元二次方程的學(xué)習(xí)，一方面，從數(shù)學(xué)內(nèi)部結(jié)構(gòu)來看，是對方程類型進行擴充，從增加方程中“元”的個數(shù)逐漸過渡到升高方程中“元”的次數(shù)，從中能感悟到知識的連續(xù)性與必然性；另一方面，從數(shù)學(xué)外部來看，方程是刻畫現(xiàn)實世界數(shù)量關(guān)系的有效模型. 對于章統(tǒng)領(lǐng)課，從數(shù)學(xué)內(nèi)部與外部兩方面厘清知識的內(nèi)在聯(lián)系，有助于學(xué)生樹立認(rèn)識事物的整體觀念［2］.

2. 運用類比思想，培養(yǎng)知識正遷移能力

方程是刻畫現(xiàn)實世界數(shù)量關(guān)系的有效模型，教學(xué)時可先從幾個簡單的實際問題中找到相等關(guān)系列出方程，歸納這一類方程的共同屬性，再與之前學(xué)習(xí)的方程類型進行對比，抽象出一元二次方程的概念. 接下來提出“大”問題——我們該怎么研究一元二次方程呢？類比思想是研究一個“新”問題的重要途徑之一，借助之前學(xué)習(xí)一元一次方程的經(jīng)驗，可類比構(gòu)建一元二次方程的研究思路，形成研究方程的一般路徑：定義—解法—應(yīng)用. 在“大”問題的驅(qū)動下，教師引發(fā)學(xué)生思考，并通過追問不斷聚焦問題，讓學(xué)生在思考與活動中積累經(jīng)驗，培養(yǎng)知識正遷移能力.

章統(tǒng)領(lǐng)課實踐過程

下面以“一元二次方程”的章統(tǒng)領(lǐng)課為例.

1. 目標(biāo)制定與目標(biāo)解析

（1）目標(biāo)

①用方程描述實際問題中的相等關(guān)系，經(jīng)歷由實際問題抽象出一元二次方程模型的過程，感受方程是刻畫現(xiàn)實世界數(shù)量關(guān)系的有效模型.

②類比一元一次方程的學(xué)習(xí)路徑，構(gòu)建一元二次方程整章知識的研究路徑，感悟類比數(shù)學(xué)思想.

③通過觀察式結(jié)構(gòu)特征，嘗試解不同形式的一元二次方程，感悟轉(zhuǎn)化數(shù)學(xué)思想，初步積累解一元二次方程的經(jīng)驗.

（2）目標(biāo)解析

目標(biāo)①達成的標(biāo)志是：能夠分析實際問題中的數(shù)量關(guān)系及其變化規(guī)律，能用方程刻畫實際問題中的相等關(guān)系.

目標(biāo)②達成的標(biāo)志是：回顧一元一次方程的學(xué)習(xí)路徑，能夠自主構(gòu)建出研究一元二次方程的大致思路.

目標(biāo)③達成的標(biāo)志是：能夠解形如（x+h）2=k（k≥0，h，k均為常數(shù)）與（x+a）（x+b）=0（a，b均為常數(shù)）的方程；能將二次項系數(shù)為1的一元二次方程用配方法化為（x+h）2=k（h，k均為常數(shù)）的形式并求解，形成解一元二次方程的一般性策略.

2. 教學(xué)過程

問題1用方程描述下列問題中的數(shù)量關(guān)系.

（1）正方形桌面的面積是2 m2. 設(shè)該正方形桌面的邊長是x m.

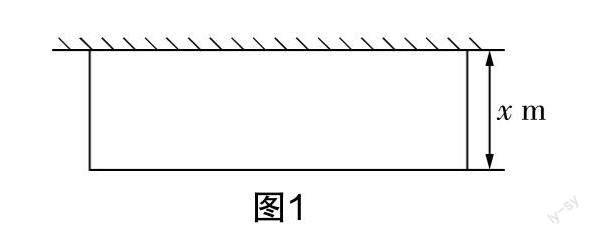
（2）如圖1所示，矩形花園一面靠墻，另外三面所用柵欄的總長度是19 m，花園的總面積是24 m2. 設(shè)花園與墻垂直的一條邊的長是x m.

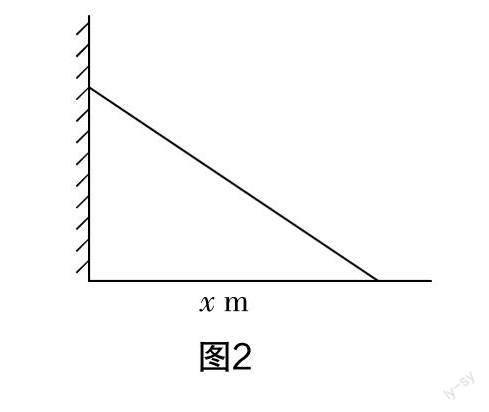
（3）如圖2所示，長5 m的梯子斜靠在墻上，梯子底端與墻的距離比梯子頂端與地面的距離多1 m. 設(shè)梯子底端與墻的距離是x m.

追問1：觀察列出的三個方程，它們與我們之前學(xué)習(xí)的方程一樣嗎？如果不一樣，最大的區(qū)別在哪里？

追問2：請化簡三個方程，化簡后按照未知數(shù)x的降冪排列.

追問3：你能給這種類型的方程起一個名字嗎？根據(jù)方程的特征并嘗試下定義，你能用一個通式表達這種類型的方程嗎？請寫一寫.

追問4：剛才我們討論了一元二次方程的定義，接下來我們會研究什么呢？

生（齊）：解法、應(yīng)用.

追問5：你們是怎么想到的？你們是從哪里獲得的經(jīng)驗？

生（齊）：從學(xué)習(xí)一元一次方程中獲得的經(jīng)驗.

設(shè)計說明“問題1”中的三個實際問題，能讓學(xué)生再一次感受到方程是刻畫現(xiàn)實世界數(shù)量關(guān)系的有效模型. 學(xué)生可以自主、快速地列出三個方程：x2=2，x（19-2x）=24，x2+（x-1）2=25. “問題1”之所以沒有在列方程上給學(xué)生設(shè)置障礙，是為了讓學(xué)生在章起始課不畏懼本章的學(xué)習(xí)，從而調(diào)動學(xué)生的學(xué)習(xí)積極性，讓學(xué)生收獲成功的喜悅，激發(fā)學(xué)生的主觀能動性.

這一形成一元二次方程概念的環(huán)節(jié)與筆者以往的教學(xué)略有不同——本次多了“追問1”的環(huán)節(jié). 列出方程后，筆者讓學(xué)生先觀察三個方程，從式結(jié)構(gòu)上直觀感受三類方程的特征，培養(yǎng)學(xué)生解決數(shù)與代數(shù)問題時需要先觀察式結(jié)構(gòu)特征的意識，并非看到式子就開始化簡，該意識的培養(yǎng)會對學(xué)生數(shù)與代數(shù)領(lǐng)域的學(xué)習(xí)產(chǎn)生重要的影響. “追問2”是為了讓學(xué)生歸納出一元二次方程的共同特征（一個未知數(shù)、未知數(shù)的最高次數(shù)是2）. “追問3”讓學(xué)生用一個通式表達一元二次方程，大部分學(xué)生第一次寫不對，此時教師不必心急，不要直接投影出正確答案，因為這是本環(huán)節(jié)的難點. 教師可以先投影出學(xué)生所寫的最特殊的通式，并與學(xué)生共同探討. 逐步對通式“豐滿”的過程能加深學(xué)生對一元二次方程式結(jié)構(gòu)的認(rèn)識. 例如，筆者執(zhí)教時先投影的是x2=a，再和學(xué)生一起逐步“豐滿”一元二次方程的通式（如圖3所示）. “追問4”與“追問5”的目的是引導(dǎo)學(xué)生類比遷移一元一次方程的學(xué)習(xí)路徑，繼續(xù)對一元二次方程展開研究，固化研究方程的“套路”.

問題2 下面我們談一元二次方程的解法. 大家觀察化簡后的三個一元二次方程（x2-2=0，-2x2+19x-24=0，x2-x-12=0），哪一個方程最“好”解？

生（齊）：x2-2=0.

追問6：嘗試解解看.

追問7：類似地，你還能寫出一些“好”解的一元二次方程嗎？

投影（學(xué)生素材1）：（x-1）2=4，這個方程“好”解嗎？

生1：根據(jù)平方根的定義可得x-1=2或x-1=-2，解得x=3或x=-1.

追問8：解方程時，如何看待（x-1）這個式子？

生2：把這個式子看成一個整體.

追問9：方程從（x-1）2=4到x-1=2或x-1=-2，這中間發(fā)生了什么變化？

生3：未知數(shù)的次數(shù)降低了，一個一元二次方程變成了兩個一元一次方程.

小結(jié)：通過開平方可將一個一元二次方程轉(zhuǎn)化成兩個一元一次方程，從而求出原方程的解；未知數(shù)的次數(shù)從二次變成了一次，這個過程叫降次（如圖4所示）.

投影（學(xué)生素材2）：2（x-1）2=4，這個方程你們會解嗎？

生4：等式兩邊同時除以2，原方程便化為（x-1）2=2，解法和之前的一樣.

追問10：那把方程改寫成2（x-1）2=-1，這個方程怎么解？

生5：無解（教師規(guī)范成了“無實根”），因為負(fù)數(shù)沒有平方根.

投影（學(xué)生素材3）：（x-1）2=0，這個方程你們會解嗎？

生6：x-1=0，解得x=1.

追問11：大家對這個方程的解有不同的看法嗎？（教室鴉雀無聲）

追問12：我們回顧一下剛才解（x-1）2=4與2（x-1）2=4這兩個方程的過程，通過直接開平方后一個一元二次方程變成了兩個一元一次方程，但方程（x-1）2=0開平方后怎么就只有一個一元一次方程了呢？

生7：可以把方程（x-1）2=0看成（x-1）（x-1）=0. 兩個因式的積為0，那么這兩個因式至少有一個為0，可得x-1=0或x-1=0，解得x=1或x=1，這其實還是轉(zhuǎn)化成了兩個一元一次方程，只是這兩個一元一次方程是一樣的.

師：為了和之前的結(jié)構(gòu)保持一致，因此，這個方程的解我們寫成x1=x2=1.

追問13：類似地，你們還能寫出一些“好”解的方程嗎？

投影（學(xué)生素材4）：（x+2）（x+3）=0，這個方程怎么解？

生8：（x+2）與（x+3）的積為0，說明x+2=0或x+3=0，解得x=-2或x=-3.

追問14：請大家觀察這些“好”解的方程，你能用通式表達這些“好”解的方程嗎？（如圖5所示）

設(shè)計說明本環(huán)節(jié)從觀察“好”解的方程過渡到寫“好”解的方程，并歸納出“好”解的一元二次方程的結(jié)構(gòu)，為后續(xù)解一般結(jié)構(gòu)的一元二次方程埋下伏筆，能讓學(xué)生感悟到從特殊到一般研究問題的方法；在探究解法的過程中，學(xué)生能感悟到一元二次方程根的個數(shù)與未知數(shù)次數(shù)之間的關(guān)系.

問題3嘗試解方程x2-8x+7=0.

追問15：這個方程和之前所解的一元二次方程有何不同？能否將其化為“好”解的一元二次方程？

設(shè)計說明對于“問題3”，筆者在執(zhí)教時先“放手”讓學(xué)生嘗試完成，當(dāng)學(xué)生遇到困難時，小組討論，教師則分步驟適時介入引導(dǎo)，讓大部分學(xué)生能解出此方程，最終師生共同總結(jié)出可以通過配方法或因式分解法將一般的一元二次方程轉(zhuǎn)化為“好”解的一元二次方程（如圖6所示），從而感受化歸數(shù)學(xué)思想解決問題的魅力.

問題4學(xué)完本節(jié)課，本章的知識結(jié)構(gòu)你們清楚了嗎？請談?wù)勀愕氖斋@.

設(shè)計說明明確“一元二次方程”這一章的知識框架，明確本章的學(xué)習(xí)路徑.

目標(biāo)檢測設(shè)計

教師可設(shè)計如下試題用于檢測目標(biāo)是否達成：

1. 已知方程（m-1）x2-（2m-1）x+m=0.

（1）當(dāng)m=______時，該方程是關(guān)于x的一元一次方程；

（2）當(dāng)m_______ 時，該方程是關(guān)于x的一元二次方程.

設(shè)計說明檢測學(xué)生對一元二次方程概念的掌握情況.

2. 解方程.

（1）2x2-8=0；

（2）3（x-1）2=6；

（3）x2-x-12=0；

（4）（2x-1）2=（3-x）2.

設(shè)計說明檢測學(xué)生對解特殊結(jié)構(gòu)的一元二次方程的掌握情況，培養(yǎng)學(xué)生用化歸思想解決問題的意識.

3. （選做題）我們學(xué)習(xí)了一元一次方程、二元一次方程（組）、三元一次方程（組），可看成一元一次方程在“元”上進行推廣；類似地，學(xué)完一元二次方程后還可能研究哪些類型的方程呢？請類比一元二次方程的研究路徑寫出該類型方程的研究路徑，并嘗試對該類型方程進行求解.

設(shè)計說明本題是考查學(xué)生能否將一元二次方程的研究路徑類比到其他類型方程的學(xué)習(xí)中. 本題為選做題，目的是給“吃不飽”的學(xué)生留有思考空間.

總結(jié)與反思

1. 滲透轉(zhuǎn)化思想，強化代數(shù)推理能力

轉(zhuǎn)化不僅是一種數(shù)學(xué)思想，還是一種最基本的解決問題的策略. 運用轉(zhuǎn)化思想可將生疏的問題變熟悉，將復(fù)雜的問題變簡單，將抽象的問題變形象. 本節(jié)課在教學(xué)一元二次方程的解法時，從解“好”解的一元二次方程過渡到解一般的一元二次方程，滲透了從特殊到一般研究問題的方法. 解一般結(jié)構(gòu)的一元二次方程時，需要將其轉(zhuǎn)化為“好”解的一元二次方程，這就是運用轉(zhuǎn)化思想解決問題形成的策略性知識. 課堂上，將方程x2+bx+c=0轉(zhuǎn)化為（x+h）2=k的過程中，教師需要放慢腳步，引導(dǎo)學(xué)生思考如何向“好”解的方程變形，有意識地讓學(xué)生關(guān)注式結(jié)構(gòu)特征，變形中做到“步步有據(jù)”，強化代數(shù)推理能力.

2. 高位建構(gòu)知識框架，把握好章統(tǒng)領(lǐng)課的“度”

上好章統(tǒng)領(lǐng)課的前提是制定精準(zhǔn)的教學(xué)目標(biāo). 章統(tǒng)領(lǐng)課的目標(biāo)需要教師自行制定，目前教參上沒有章統(tǒng)領(lǐng)課的教學(xué)設(shè)計與教學(xué)目標(biāo)，這便需要教師研究教材，揣摩編者的意圖，站在高位去建構(gòu)知識之間的內(nèi)在邏輯聯(lián)系，教師還需要思考如何將這種高位的認(rèn)識設(shè)計成學(xué)生易于接受的課堂活動. 一章的知識點很多，章統(tǒng)領(lǐng)課若面面俱到，就會變成一節(jié)“高濃度”知識點介紹課，不利于學(xué)生的發(fā)展. 因此，教學(xué)中如何把握好章統(tǒng)領(lǐng)課的“度”尤為重要. 筆者在本節(jié)課中讓學(xué)生先感受到一元二次方程是刻畫現(xiàn)實世界數(shù)量關(guān)系的有效模型，再找到該類型方程的共同屬性，最后形成一元二次方程的概念. 接下來以“好”解的一元二次方程為載體構(gòu)建解法，學(xué)生有平方根的學(xué)習(xí)經(jīng)驗，以此為突破口建立解法，最終以化歸思想為落腳點，這正是解不同類型方程的“精髓”. 筆者實踐后發(fā)現(xiàn)，學(xué)生易于接受，且效果較好. 一節(jié)課的時間有限，筆者沒有將二次項系數(shù)不為1的一元二次方程納入本節(jié)課，況且學(xué)生學(xué)習(xí)知識具有連續(xù)性與階段性，如果學(xué)生將解二次項系數(shù)為1的一元二次方程的過程“悟”透徹，那他們解二次項系數(shù)不為1的一元二次方程自然是“水到渠成”.

3. 精準(zhǔn)設(shè)計章統(tǒng)領(lǐng)課作業(yè)，助力提升核心素養(yǎng)

精準(zhǔn)設(shè)計作業(yè)是檢測課堂教學(xué)效果的前提，本節(jié)課的作業(yè)設(shè)計了三道題，第一道題用于檢測學(xué)生對一元二次方程概念的理解. 第二道題用于檢測學(xué)生解不同形式的一元二次方程的掌握情況，特別地，解（2x-1）2=（3-x）2時有三種思路，第一種是通過去括號、移項、合并同類項之后發(fā)現(xiàn)這是一個二次項系數(shù)不為1的一元二次方程，教師批改作業(yè)時要特別關(guān)注學(xué)生會不會將二次項系數(shù)轉(zhuǎn)化為1去求解，是否有轉(zhuǎn)化的意識，這便在作業(yè)中留下本節(jié)課的第一條“生長鏈”；第二種是將方程右邊（3-x）2移項到方程的左邊后因式分解成（x+a）（x+b）=0的結(jié)構(gòu)去求解；第三種是基于學(xué)生之前的學(xué)習(xí)經(jīng)驗——若a2=b2，則a=b或a=-b. 講評作業(yè)時，教師要讓學(xué)生意識到第一種解法是“通法”，后面兩種解法是由于這個方程具有特殊的式結(jié)構(gòu). 由此總結(jié)出解方程的第一步是觀察而非化簡. 第三道題是選做題，目的是讓學(xué)有余力的學(xué)生自主構(gòu)建一元三次方程（或其他類型方程）的研究路徑，并嘗試求解，培養(yǎng)學(xué)生的自主學(xué)習(xí)能力，這就在作業(yè)中又一次留下本節(jié)課的“生長鏈”.

結(jié)束語

章統(tǒng)領(lǐng)課中“統(tǒng)”的是知識的整體性，在構(gòu)建知識框架過程中感受知識發(fā)展的必然性；“領(lǐng)”的是數(shù)學(xué)思想及策略；在“統(tǒng)”和“領(lǐng)”的驅(qū)動下提升能力，促進核心素養(yǎng)的養(yǎng)成. 顯然，一次章統(tǒng)領(lǐng)課是遠遠不夠的，學(xué)生在學(xué)習(xí)每一章之前都經(jīng)歷一次系統(tǒng)構(gòu)建本章知識框架的過程，能逐步增強運用數(shù)學(xué)思維解決問題的意識，能逐步形成正確的價值觀、必備品格與關(guān)鍵能力，從而發(fā)揮數(shù)學(xué)學(xué)科的育人價值.

參考文獻：

［1］中華人民共和國教育部. 義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）［M］. 北京：北京師范大學(xué)出版社，2022.

［2］楊春霞. 基于整體性架構(gòu)教學(xué)，凸顯數(shù)學(xué)學(xué)科核心素養(yǎng)［J］. 中學(xué)數(shù)學(xué)，2020（10）：24-26.