感悟數形結合思想　提升數學核心素養

劉劍華

摘 要：數形結合思想作為重要的數學思想，其有利于學生掌握數學學習方法，讓學生獲得更好的學習體驗，提升學生學習品質.在二次函數的復習教學中，教師精心創設問題鏈，讓學生在問題的引領下積累研究函數的數學活動經驗，領悟數學研究中蘊含的數形結合的思想，著力提高學生的數學核心素養.

關鍵詞：數形結合思想；學習品質；數學核心素養

在每章內容學習后，教師大多會安排時間進行單元復習，以便通過有效的復習幫助學生建構完善的知識體系，提煉數學思想方法，提升學生解決問題的能力.筆者以“二次函數的復習課”為例，通過數形結合思想方法的滲透，提高教學有效性讓學生較好地感悟思想、理解數學.

1 教學分析

二次函數的復習課安排在本章內容全部學完后，通過有效地回顧、思考、總結歸納本章教學的重難點，讓學生掌握數學研究方法，提升學生自主學習能力.二次函數在初中數學教學中具有舉足輕重的地位，其既有利于學生進一步理解函數的概念，又為后期學習一元二次不等式奠定了基礎.

從教學反饋來看，學生在解題時大多是從“數”的角度出發，習慣運用代數的方法解決問題，從而使得運算過程煩瑣，影響了解題效果.其實，學生之所以數形結合意識不強也與教師的教息息相關，大多教師對數形結合的認識不夠充分，導致課堂上數學思想方法的滲透流于形式，導致學生對知識的理解不夠深刻，難以靈活應用相關知識解決問題，影響了解題效果.因此，在復習課教學中，教師可嘗試通過適度的啟發和引導讓學生逐漸感悟數形結合思想，激發學生參與課堂的積極性，提高教學效率.

2 教學簡述

2.1 內容回顧，體驗數形結合思想

師：對于數形結合的思想方法大家并不陌生，誰來說一說，應用數形結合有什么好處呢？

生1：“形”比較直觀，利用“形”可以開闊視野，拓寬思路.不過“形”不夠嚴謹，需要以“數”為依托，兩者相互聯系，相互依存.在解題時合理應用數形結合可以快速形成思路，提高解題效率.

師：說得很好，今天我們就用數形結合的思想來復習二次函數的圖象和性質.

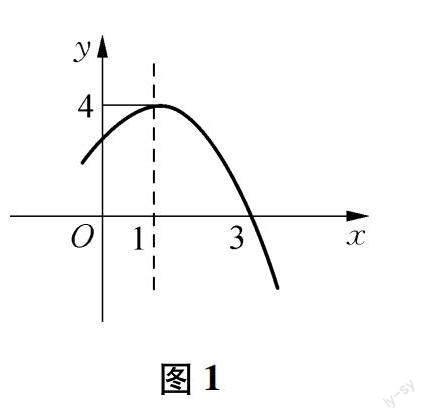
師：圖1是拋物線y=ax²+bx+c（a≠0）的圖象，結合圖象說一說，你能得到什么結論？

生1：與x軸交點坐標分別為（3，0）和（-1，0），頂點坐標為（1，4）.

師：很好，還有其他發現嗎？

生2：圖象開口向下，故a＜0；對稱軸位于y軸的右側，而a＜0，根據左同右異原則可知b＞0；圖象與y軸的交點位于y軸的正半軸，故c＞0.

師：很好，觀察得非常仔細.請大家繼續觀察，看看還能得到哪些信息？（生沉思）

生3：根據以上發現可以圖象有最大值，且最大值為4；圖象與x軸有兩個交點，所以有b²-4ac＞0；根據頂點式易求得二次函數表達式y=-（x-1）²+4.

師：很好，你剛剛是利用哪兩個點得到二次函數的

頂點式表達式的呢？

生4：利用頂點（1，4）和與x軸交點（3，0）.

師：如果把二次函數y=-（x-1）²+4向左平移1個單位，向下平移4個單位，你會得到一個什么樣的二次函數？

生5：平移后圖象的對稱軸為y軸，頂點坐標為（0，0），得到的二次函數的解析式為y=-x².

師：很好，如果把二次函數y=-x²向上平移6個單位，你得到的二次函數解析式是什么？把二次函數y=-x²向右平移3個單位呢？

生6：兩個函數分別為y=-x²+6和y=-（x-3）².

師：結合以上平移過程，請大家總結歸納一下，函數圖象的平移遵循的什么原則？

生齊聲答：左加右減，上加下減.

師：剛剛這位同學結合函數圖象特點，利用頂點式得到了二次函數表達式，是否可以用其他方法得到二次函數表達式呢？

生4：已知二次函數與x軸交點坐標分別為（3，0）和（-1，0），故可以應用交點式求出二次函數表達式.

生7：已知二次函數與x軸交點坐標分別為（3，0）和（-1，0），頂點坐標為（1，4），所以還可以利用一般式來求二次函數的表達式.

師：很好，大家現在動手做一做，看看利用其它兩種方法求出的二次函數解析式是什么？本題應用哪種方法最方便呢？

設計意圖：教師預留充足的時間讓學生觀察，盡量多地挖掘已知信息，這樣既幫助學生回顧了舊知，促進了知識的鞏固，又為接下來多角度探究奠定了基礎.在此過程中，教師精心創設問題鏈，讓學生在問題的引領下自主探究、合作交流，總結歸納圖象的平移遵循的法則，并自然得出了二次函數的另外兩種表達方式，促進了學生認知體系的建構與完善^［1］.

師：觀察圖1，你還能挖掘出其他的信息嗎？

生8：令圖象與y軸的交點為點C，其坐標為（0，3），點F與點C關于x=1對稱，其坐標為（2，3），直線CF平行于x軸.

師：你是如何求點C的坐標的呢？（師追問）

生8：我是利用解方程的方法求解的，將x=0代入函數解析式，解得y=3.

師：很好，利用數形結合發現了二次函數與一元二次方程的聯系，那么它與一元二次不等式呢？兩者是否存在一定的聯系呢？

設計意圖：借助問題，將二次函數，一元二次方程和一元二次不等式建立聯系，讓新、舊知識相互溝通，豐富學生已有認知，鍛煉學生觀察能力、分析能力和遷移能力.

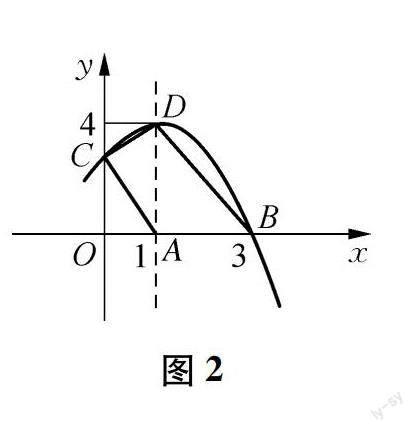
師：若從線段的角度去思考，你又有什么發現？（為了便于表述，教師給出圖2）

生9：OA=1，OB=3，OC=3.結合已知，根據勾股定理，易求線段AC的長.

師：思考一下，四邊形ABDC的面積是否可求呢？

問題給出后，學生積極思考，分別求出S_△AOC，S_梯形AOCD，S_△BAD的面積，問題即可獲解.

設計意圖：引導學生從不同角度挖掘圖象信息，鍛煉了學生“動腦”“動口”的好習慣，充分調動了學生參與活動的積極性，讓學生在自主學習和合作交流中獲得了可持續發展的能力，提高了學生數學素養^［2］.

在以上教學活動中，教師以學生的發現為主線，有組織、有目的、有針對性地引導學生進行探索研究，側重于學生能力的提高和思維的訓練，提高了學生綜合能力和綜合素養.

2.2 引導探究，感悟數形結合思想

師：若想使該拋物線經平移后通過坐標原點，可以如何平移呢？

生10：可以左右平移，向左平移3個單位或向右平移1個單位.

師：分別作該拋物線關于x軸和y軸的軸對稱圖形，你能求出對應拋物線的解析式嗎？

（為了降低問題的難度，教師將問題進行拆分，通過分步引導，幫助學生形成策略）

師：我們先來分析關于y軸的軸對稱圖形，它的開口方向、開口大小如何變化，其對稱軸及與y軸的交點又是什么呢？（教師鼓勵學生通過動手畫尋找解題思路）

生11：開口方向、開口大小、與y軸交點均不變，所以a和c的值也不變.對稱軸由直線x=1變成了x=-1，根據左同右異得b=-2，所以拋物線的解析式y=-x²+2x+3關于y軸的軸對稱圖形的解析式為y=-x²-2x+3.

在此基礎上，學生通過分析開口方向、開口大小、與y軸交點等內容，求得該拋物線關于x軸的軸對稱圖形的解析式為y=x²-2x-3.

師：若將拋物線y=-x²+2x+3繞它的頂點旋轉180°，你還能求出拋物線的解析式嗎？

設計意圖：通過平移變換、軸對稱變換、旋轉變換，讓學生在變換中更好地體驗數學，培養思維的靈活性，鍛煉學生思維，增強學生學習信心，讓學生在合作研究中更好地體驗數形結合思想，發展學生數學學習能力.

2.3 課堂小結，升華認知

師：通過本課的復習，你學到了什么？還有哪些困惑？

教師預留時間讓學生進行反思、回顧，并鼓勵學生進行組內交流.

設計意圖：通過反思、交流引導學生對學習內容進行梳理，從而使學生掌握的知識更加系統化、條理化，既便于學生理解與記憶，又促進了知識的遷移與重構，有利于提高學生綜合應用能力^［3］.在此環節，教師引導學生對獲取知識中涉及的思想、方法、策略進行反思，以此深化知識理解，積累活動經驗，明確數形結合思想.另外，通過小結可以讓教師更好地了解學生之所思、之所獲、之所難，從而為針對性教學活動的創設提供了教學依據，有利于提高教學有效性.

3 教學思考

在本課教學中，教師以數形結合思想為核心，通過創設合理的問題情境將二次函數二項性質、三種表示、平移變換、軸對稱變換、旋轉變換等內容有效地關聯在一起，通過潛移默化的啟發和引導幫助學生建構了完善的知識體系.同時，本課教學中，教師貫徹以生為主導，以生為主體的教育理念，打破了傳統講授的枯燥與乏味，讓學生體驗了自主探究的樂趣，并讓學生在自主探究中獲得了知識、掌握了技能，明確數形結合思想，提升了數學素養.

總之，在復習教學中，教師不僅要關注于知識與技能的提升，也要關注學生對數學思想方法的理解和感悟.在教學中可以創設有效的問題情境讓學生去思考、去探索、去提煉，以此提升學生自主學習能力，發展學生數學核心素養.

參考文獻：

［1］ 張海芳.初中數學教學中數形結合思想的滲透［J］.數學大世界：上旬，2021（3）：90-91.

［2］ 徐春華.核心素養下初中數學生本課堂的構建研究［J］.科學咨詢，2019（9）：146.

［3］ 巨彥春.初中數學教學中數學學科核心素養滲透路徑探究［J］.中學數學：初中版，2021（18）：86-87.