高中數學平面向量解題教學過程中的一點思考

張椿悅

摘要：數學課堂離不開解題教學，數學解題能力的訓練離不開扎實的基礎知識的支撐.本文中從教師層面提出了關于在教學過程中提升學生數學解題能力的一點思考，并以平面向量習題為具體實例進行闡述，要提高學生的解題能力必須夯實基礎、引導學生從多角度分析問題，實現知識互聯.

關鍵詞：高中數學；解題教學；平面向量

普通高中數學課程標準指出，學科核心素養是育人的集中體現，解題教學是提高學生數學核心素養的重要途徑之一.教師要注重對教材內容的解讀與分析，夯實學生基礎知識，提高學生數學抽象能力；同時，教師不僅要向學生傳授教材基本知識，還要引導學生拓展解題技巧，培養數據分析、邏輯推理能力.在解題教學過程中，設置適合學生認知發展水平的問題，關注學生思維的發展，重視一題多解，引導學生總結一般的解題方法并思考可能的特殊方法，有意識地向學生滲透常用的數學思想方法，以此在教師維度關注學生思維發展，提升學生解題能力.

1 夯實基礎知識，構建聯想基礎

基礎知識的運用是解題過程中最為關鍵的一個環節，無論對何種水平的學生來說都是至關重要的.沒有牢固的基礎知識作支撐，學生無法在題目中抽象出數學概念、建立適當的數學模型，也會由于無法調動舊知而在解題過程中繞圈子.有些優等學生認為做基礎題是浪費時間，但作為教師要認識到并不是只有難題才是“好題”.有時也難免會有一些優秀學生因為過于關注難題的訓練而忽視了基礎的重要性，在面對一些常規問題時繞不出來“難”的怪圈，把簡單問題復雜化.

本題考查平面向量數量積運算（非坐標）、數量積定義、三角形的垂心及平面向量共線的知識.應用平面向量共線定理，結合平面向量運算的知識可以求得三角形邊AB，AC的關系.解決本題的先決條件是學生要對平面向量共線定理及其推論非常熟悉，識別出共線的“爪形”結構，從而通過已知條件推出三角形的邊AB，AC的關系，進而解題.本題也反映出扎實掌握基礎知識、理解本質、熟悉知識的結構與形式將更有助于提高學生數學抽象、直觀想象等能力，所以教師在教學過程中要充當好引導者的角色，重視學生對基礎知識的內化，習題講解時注重設置問題情境，啟發學生思考.[HJ1.3mm]

2 “通法”雪中送炭，“巧解”錦上添花

所謂通法，通常指解決某類問題的常規方法，這類方法以基礎知識為依據，往往容易理解，對大多數學生來說也容易掌握.“巧解”的關鍵在于“巧”，對于某類習題也可以打破常規，化繁為簡，避開某些通法所涉及到的冗長計算，這種方法靈活性強，有助于訓練學生的發散思維.教學過程中教師應該重視一題多解，在重基礎、講通法的同時，也要兼顧到“巧解”的引導和介紹.注意“巧解”并非是萬能的，要引導學生在重視通法的基礎上兼顧巧解，否則可能會導致弄“巧”成拙的局面，即通法一觸即發，而固化思維卻一直在尋求所謂的“巧解”.

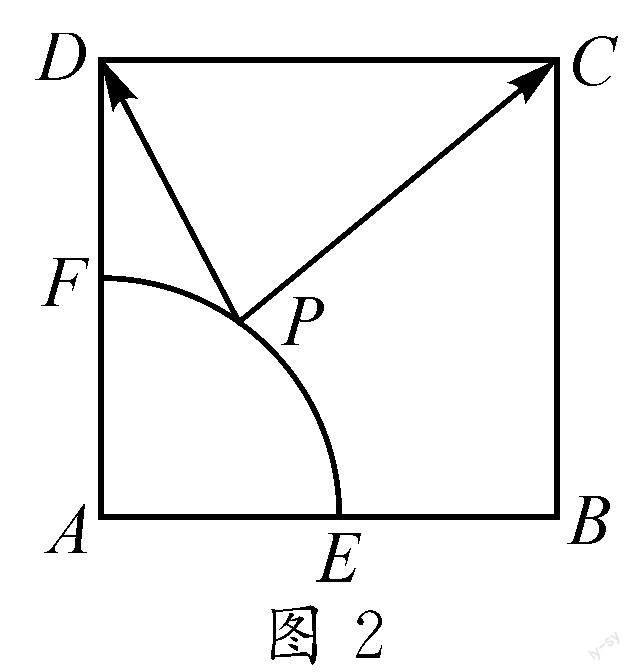
分析：有關數量積取值范圍的問題可采用坐標法或基底法來解決.題目中有正方形模型，存在天然的建系條件，可以通過建系，設動點P的坐標，將問題轉化為定點到圓弧上點的距離取值問

本題解法靈活多樣，教學過程中要強調一題多解，引導學生從多角度分析問題，讓他們在同一數學情境中強化對基礎知識的靈活運用.

例4 已知a，b是單位向量，a·b=0，若c滿足|c-a-b|=1，求|c|的取值范圍.

分析：本題設有單位向量且二者垂直，可聯想到坐標法，設點C的坐標，由|c-a-b|=1求出|c|的范圍.由于向量模塊集幾何與代數于一體，很多問題都可以通過幾何與代數相結合的形式來破解，如本題也可通過畫出c，a+b構成的向量三角形求解.

解法一：由題意知單位向量a，b垂直，不妨設a=（0，1），b=（1，0）.

解法三：從代數角度分析.

記c-a-b=d，則c=a+b+d.

3 提高數學素養，實現知識互聯

數學家泰勒曾說過：“有豐富知識和經驗的人，會比只有一種知識和經驗的人更能產生新的想法和獨到的見解.”良好的聯想能力能夠促進學生對知識、方法、經驗的遷移.在教學中，運用已有認知結構中的知識聯想解題策略，引導學生通過在已有的探究活動過程中積累的經驗聯想解題方法和數學思想，感受數學思想的運用與遷移.在整個教學環節中強化學生對數學思想方法的積累，加強他們在學習知識的過程中對活動經驗的體驗和感受，培養聯想意識.