“多邊形的面積”復習教學，應關注空間維度

王加林

摘 要：教學“多邊形的面積”后，設計一節復習（拓展）課，引導學生重新推導平行四邊形、三角形、梯形的面積公式，梳理多邊形面積公式之間的關系，進而歸納發現面積的二維屬性，類比發現周長的一維屬性，并發散認識空間的維度，從而幫助學生更好地理解面積概念，區分周長與面積，發展空間觀念。

關鍵詞：小學數學；面積；周長；空間維度；多邊形的面積

一、教前思考

周長和面積是小學數學中比較容易混淆的兩個概念。學生（使用蘇教版小學數學教材）在三年級上學期學習周長概念以及長方形和正方形的周長，在三年下學期學習面積概念以及長方形和正方形的面積，然后在五年級上學期學習平行四邊形、三角形、梯形等多邊形的面積。教學面積概念后，可以從定義和度量兩個角度，引導學生比較辨析周長和面積的聯系和區別。時隔一年半，教學“多邊形的面積”后，學生對“周長和面積的聯系和區別”掌握得如何？筆者在課后作業中設計了一道有關周長和面積的練習：

把一個用鐵絲圍成的長方形框架拉成一個平行四邊形，該框架的周長和面積發生了什么變化？

對此，筆者所教班級以及同年級其他班級學生的答題情況統計如下頁表1所示。可見，學生的錯誤率不低，這反映出他們對周長和面積的聯系和區別掌握得不是很好。進一步訪談得知：學生知道周長和面積的描述性定義、度量方法以及計算方法（數或算出度量單位的個數），有比較好的量感；但是，對二者度量本質（聯系）下的空間維度屬性（區別）理解得不透徹。

實際上，“幾何學起源于圖形大小的度量……根據圖形的維數，把度量一維圖形大小的數稱為長度，將二維圖形的大小用面積來表示……”［1］。但是，小學數學教材對長度、面積等的維度屬性介紹得并不多。張奠宙先生就曾指出：小學教材中對長度、面積和體積的維度屬性認識不足，導致學生對線段、平面、立體的區分及關聯有些疏漏，甚至出現錯誤。［2］

因此，教學“多邊形的面積”后，筆者設計了一節復習（拓展）課，引導學生重新推導平行四邊形、三角形、梯形的面積公式，梳理多邊形面積公式之間的關系，進而歸納發現面積的二維屬性，類比發現周長的一維屬性，并發散認識空間的維度，從而幫助學生更好地理解面積概念，區分周長與面積，發展空間觀念。

二、教學過程

（一）重新推導平行四邊形、三角形、梯形的面積公式

教材引導學生通過剪拼的方法把平行四邊形轉化為長方形，從而得到平行四邊形的面積公式；然后，通過拼接兩個相同的三角形的方法把三角形轉化為平行四邊形，從而得到三角形的面積公式；最后，通過拼接兩個相同的梯形的方法把梯形轉化為平行四邊形，從而得到梯形的面積公式。這樣做有幾個不自然的地方：三角形更簡單、更基本，為什么不先推導三角形的面積公式？推導平行四邊形的面積公式時，為什么要沿著高剪下（分割）？剪下后，為什么還要移拼？這并不容易想到。推導三角形、梯形的面積公式時，怎么想到“加倍”后拼接？這和推導平行四邊形面積公式的思路并不一致。其中最關鍵的是：高的得出不自然。這不容易讓學生感受到高的重要性，進而發現面積的二維屬性：兩個互相垂直的線段的長度（一維度量）相乘的結果。

因此，筆者引導學生重新推導平行四邊形、三角形、梯形的面積公式：回到由面積單位度量得到的長方形面積公式，發現直角三角形的面積是其一半；對于一般三角形，想到作高將其分割為兩個直角三角形；對于平行四邊形，想到作高將其分割為兩個直角三角形和一個長方形；對于梯形，想到作高將其分割為兩個直角三角形和一個長方形。這樣不僅使思路更自然，而且凸顯了高的重要性，有利于學生發現面積的二維屬性。

（二）歸納總結，發現面積的二維屬性

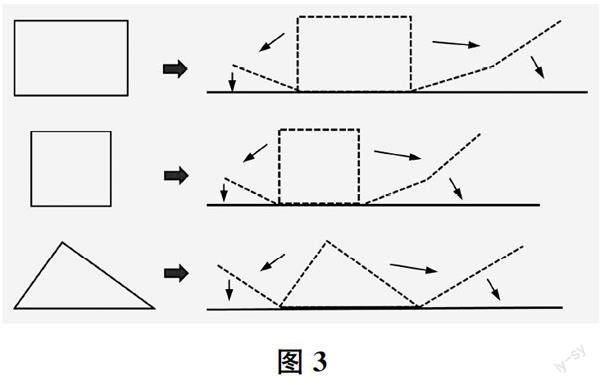
師 我們學習了長方形、三角形、平行四邊形以及梯形的面積公式。（出示圖1）觀察這幾個圖形及其面積公式，說一說它們有什么相同之處？

生 我發現，長方形和平行四邊形的面積公式都是將水平方向的長度與垂直方向的長度相乘。比如，長方形的長表示圖形水平方向的長度，寬表示垂直方向的長度，相乘得到面積；平行四邊形的底表示圖形水平方向的長度，高表示垂直方向的長度，相乘得面積。

生 我發現，三角形的面積公式也有這樣的特點：將兩個互相垂直的長度，也就是底和高相乘。

師 那為什么計算三角形的面積還要除以2呢？

生 三角形的面積是轉化成平行四邊形或長方形來計算的，它的面積是轉化后的平行四邊形或長方形的一半。

師 很好！那梯形的面積公式呢？是不是也有這樣的特點？

生 我覺得，梯形的面積公式也可以這樣理解：“上底+下底” 其實是一個量，就是水平方向的長度；高則是垂直方向的長度。它除以2的原因和三角形是一樣的。

師 沒錯！由此，我們可以發現面積的二維屬性：所有平面圖形的面積歸根到底都是其中互相垂直的兩個線段的長度（即兩個維度）相乘的結果。

有了多個平面圖形的面積公式，歸納總結其共性，發現面積概念度量本質下的二維屬性，正當其時。由此，學生可以深刻理解面積概念，特別是面積的量綱，以及說平面是二維的、稱平面圖形為二維圖形的道理。

（三）類比遷移，發現周長的一維屬性

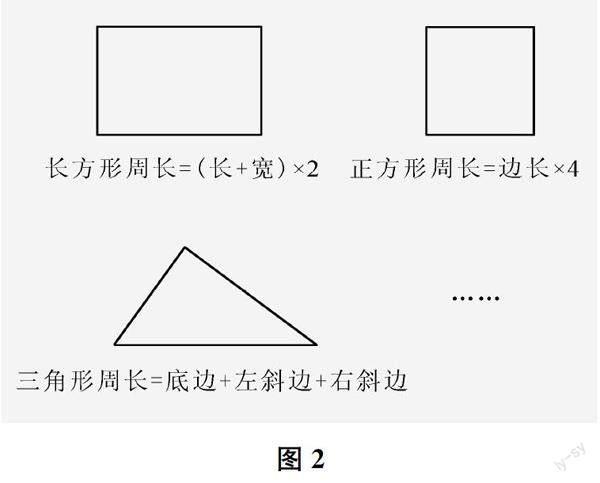
師 同學們，我們發現了平面圖形面積的二維屬性。那我們之前學習過的周長呢？（出示圖2，省去了平行四邊形、梯形的周長計算）來回顧一下周長公式，其中有什么秘密？

生 我發現，長方形的周長是長與寬的和乘2，公式中有長與寬兩個相關量；正方形的周長是邊長乘4，公式中只有邊長這一個相關量；三角形的周長是三條邊相加，有三個相關量。這三個圖形的周長公式好像沒有什么共同點。

……

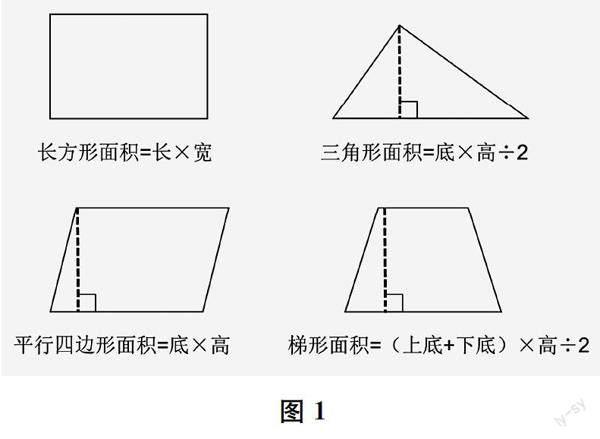
師 同學們，其實周長就是圖形一周的長度之和。（出示圖3）我們可以把長方形、正方形、三角形的周長像這樣展開，得到一條長長的線。類比面積的二維屬性，你有什么發現？

生 周長就是一些線段的長度之和。雖然這些線段的方向不同，但是我們可以把這些線段像這樣展開到同一個方向，如此，周長就是這些線段連起來后的線段的長度了。

師 是的。也即是說，周長歸根到底是一條線段的長度。這就是周長的一維屬性。現在，你能很好地區分周長和面積了嗎？

生 面積是二維的，它是圖形中互相垂直的兩個長度相乘的結果。周長是一維的，它是圖形中一些線段的長度之和。

認識了面積的二維屬性，類比遷移到周長的維度屬性，發現其是一維的，能幫助學生進一步理解面積（二維）與周長（一維）的區別，掌握圖形維度的含義。在學生觀察公式沒有發現共性的情況下，教師適時演示周長的展開，激活了學生的思維，促進了學生對周長一維屬性的理解。

（四）發散聯系，進一步認識空間的維度

師 同學們，大約在五六千年前，古埃及人在測量土地時，就認識到要從長和寬兩個維度來認識面積，由此慢慢地產生了幾何學。后來，《幾何原本》中，就有“線段是一維的，以長度來度量；平面圖形是二維的，以面積來度量；立體圖形是三維的，以體積來度量”的內容，初步有了維度概念。那么，你在生活中有沒有看到過或聽到過有關維度的內容？

生 我經常去電影，3D電影就是三維的，因為看普通電影時，我們只能從屏幕上感受到上下、左右兩個維度的方向；而看3D電影時，還能感受到前后這個方向，有的人物就像是從畫面上走出來的，離你越來越近。

生 我有一次看科學展，看到了3D打印機，它打印出來的東西不像普通打印機打印出來的那樣只在平面上，而是立體的，很真實，也就是三維的，有前后、左右和上下三個維度的方向。

師 其實，我們的數學教材中也有許多關于一維、二維、三維的知識，你發現了嗎？

生 我們學過確定位置，一年級學習的確定位置只在一個方向上，是一維的；四年級學習的是在平面上確定位置，是二維的，用數對表示——數對中一個數表示行，是水平方向的；另一個數表示列，是垂直方向的。我覺得，將來還會學習在立體空間中確定位置，即三維的。

師 是的。在立體空間中確定位置要用到三個維度，不僅要表示前后、左右，還要表示上下。

認識了一維和二維，自然可以拓展到三維。學生在生活中早就看到過或聽到過維度以及一維、二維、三維的說法，但是對它們的理解還不是很到位。因此，本環節聯系歷史、生活和數學學習，讓學生進一步理解維度，從而激發學生的學習熱情，為中學進一步學習有關維度的知識（如平面直角坐標系和空間直角坐標系、平面向量的基底和空間向量的基底）做好鋪墊。

參考文獻：

［1］ 吳正憲，劉勁苓，劉克臣.小學數學教學基本概念解讀［M］.北京：教育科學出版社，2014：325.

［2］ 張奠宙.淺而不錯、分而不碎，著眼于數學素質的養成——以“維度”概念為例［J］.小學教學（數學版），2014（12）：4-6.