“搬家法”構(gòu)造輔助線解平面幾何問題例談

鄒盈欣

摘要：作輔助線來解幾何問題是初中數(shù)學(xué)常用的解題方法，本文中利用“搬家法”的思維來快速構(gòu)造全等三角形，不僅拓寬了學(xué)生的解題思路，而且提高了解題效率.

關(guān)鍵詞：輔助線；搬家法；解題方法

通過作出輔助線構(gòu)造全等三角形是初中幾何問題的主要解題方法.很多題目會(huì)給出兩條線段相等的條件.當(dāng)給出的兩條等線段共頂點(diǎn)、共直線時(shí)，學(xué)生通常會(huì)快速地畫出輔助線，構(gòu)造出全等三角形并成功解題.然而，當(dāng)給出的兩條等線段在圖形中相隔距離遠(yuǎn)，且沒有共頂點(diǎn)、共直線時(shí)，學(xué)生往往沒了思路，感覺無從下手，有時(shí)會(huì)胡亂添加輔助線，反而使圖形越來越復(fù)雜，解題時(shí)間會(huì)跟著錯(cuò)誤的輔助線一再消耗.此類幾何題目可以出現(xiàn)在多種題型中，包括求角度、逆等線、將軍飲馬、半角模型、三角形旋轉(zhuǎn)等題型.

在解答這類兩條等線段條件的幾何題目時(shí)，筆者總結(jié)出一種創(chuàng)新思考方法——“搬家法”，其本質(zhì)就是將以其中一條等線段為邊的三角形“搬家”到另一條等線段上，搬家過去的三角形自然是全等，進(jìn)而快速解決問題.當(dāng)然，當(dāng)已知兩條等線段有連接要素，包括共頂點(diǎn)、共直線時(shí)，也可以使用“搬家法”構(gòu)造全等.

“搬家法”可以大幅減少學(xué)生的思考時(shí)間，掌握“搬家法”思維，學(xué)生可以快速構(gòu)造輔助線，提高解題效率.

下面以幾種經(jīng)典模型為例來介紹“搬家法”的應(yīng)用.

1 半角模型和旋轉(zhuǎn)例題

例1如圖1，正方形ABCD中，BM和DN分別是正方形兩個(gè)外角的平分線，且∠MAN=45°，求證：BM2+DN2=MN2.

分析：這道題的常規(guī)思路是發(fā)現(xiàn)已知條件中的半角模型，再聯(lián)想旋轉(zhuǎn)構(gòu)造全等.這個(gè)思路對(duì)學(xué)生的模型掌握、思維能力都有一定的要求.“搬家法”思路如下：

圖中標(biāo)有共同頂點(diǎn)A的三角形共有△ABM，△ADN，△AMN三個(gè)，其中△ABM，△ADN中有AD，AB兩條等線段.那么將以AD為一邊的△ADN搬家去AB邊上，或?qū)⒁訟B為一邊的△ABM搬家去AD邊上，分別得到圖2和圖3.

“搬家”后的三角形自然是全等的，即圖2中的△ADN≌△ABN′，圖3中的△ABM≌△ADM′.分別連接MN′，M′N后，學(xué)生也不難觀察到圖2中△AMN≌△AMN′（SAS），圖3中△AMN≌△AM′N（SAS），進(jìn)而觀察到所需求證的三條線段BM，DN及MN分別等量代換成圖2中△BMN′中的BM，BN′及MN′和圖3中△DM′N中的DM′，DN及M′N.

在圖2中，由已知條件可得∠ABN′=∠ADN=∠ABM=90°+45°=135°，所以∠MBN′=90°.在Rt△BMN′中，由勾股定理證得BM2+BN′2=MN2.

在圖3中，由已知條件可得∠ADM′=∠ABM=∠ADN=90°+45°=135°，所以∠M′DN=90°.在Rt△M′DN中，由勾股定理證得DN2+DM′2=M′N2.

故可證明BM2+DN2=MN2.

2 求角度例題

例2如圖4，等腰三角形ABC中，AB=AC.∠A=20°.AD=BC.求∠CDB的度數(shù).

分析：本題作為經(jīng)典考題，給出的關(guān)鍵條件是AD=BC.而AD，BC這兩條等線段沒有關(guān)聯(lián)點(diǎn).網(wǎng)絡(luò)教學(xué)視頻給出了大量不同思路的講解，輔助線的構(gòu)造方法更是層出不窮，但都沒有講解究竟怎樣才能讓學(xué)生想到構(gòu)造輔助線.通過“搬家法”，學(xué)生可以基本無需思考即可作出多種輔助線.

“搬家法”思路如下：

觀察以這兩條等線段AD，BC為邊的三角形有△ADC，△ABC和△BCD.將以AD為一邊的三角形搬家到BC邊上，或?qū)⒁訠C為一邊的三角形搬家到AD邊上，即可作出輔助線.

如將以AD為一邊的△ADC搬家到另一條等線段BC上，得到圖5和圖6.

圖5中，由于“搬家”后的三角形是全等的，學(xué)生也不難觀察到△BCC′≌△DAC，所以∠BCC′=20°，CC′=AC.由已知條件可得∠ABC=∠ACB=80°，則∠ACC′=60°.連接AC′后可得等邊三角形ACC′及等腰三角形ABC′，所以∠BAC′=∠CAC′-∠CAB=40°.在等腰三角形ABC′求得∠ABC′=∠AC′B=70°，所以∠ACD=∠CC′B=∠AC′B-∠AC′C=70°-60°=10°.故∠CDB=∠ACD+∠BAC=20°+10°=30°.

圖6中，△BCC′≌△ADC.連接AC′后可得等邊三角形ABC′及等腰三角形ACC′，進(jìn)而觀察到含有60°的等腰三角形ACC′及三角形ABC′.通過等邊三角形的角輕松求出答案.

同樣的搬家道理，也可以將以BC為一邊的△ABC搬家到另一條等線段AD上，得到圖7.“搬家”后得到△ABC≌△A′AD.學(xué)生同樣很容易連接CA′得到等邊三角形AA′C，進(jìn)而求出答案.

例3如圖8，AB=AD=BC，∠ABC=90°，∠BAD=30°，求∠C的度數(shù)

分析：此題常規(guī)解題思路是以AB，BC為邊補(bǔ)齊正方形，通過對(duì)角線性質(zhì)再求解.對(duì)于八年級(jí)上學(xué)期的學(xué)生來說很難求解，但連接BD后，通過“搬家法”也可以輕松求解.連接BD后，由已知的重要條件AB=AD=BC來觀察這三條等線段上的三角形只有△ABD和△BDC.“搬家法”的思路是把△BCD搬到AB邊上（如圖9），或是把△ABD搬到BC邊上（如圖10和圖11）.

在圖9中，由已知條件得到∠ABD=∠ADB=75°，∠CBD=90°-75°=15°.把△BCD搬到AB邊上，則△BCD≌△BAD′，于是得到∠BAD′=∠BCD，∠ABD′=∠CBD，BD=BD′.故∠ABD′=∠CBD=15°，那么∠DBD′=60°，隨即得到△BDD′為等邊三角形，即BD=BD′=DD′.所以△ABD′≌△ADD′（SSS），于是∠BAD′=∠DAD′.又已知∠BAD′+∠DAD′=30°，所以∠BCD=∠BAD′=15°.

在圖10中，由已知條件得到∠ABD=∠ADB=75°，∠CBD=90°-75°=15°.把△ABD按圖10搬到BC邊上后，△ABD≌△BCD′，∠CBD′=∠BAD=30°，所以∠DBD′=∠CBD′-∠CBD=15°，∠ABD′=90°-30°=60°，所以△ABD′為等邊三角形.隨即得到AF為等邊三角形△ABD′的BD′邊上的三線合一的中線.再過點(diǎn)D作BC的垂線，垂足為E，不難證明△BDE≌△BDF（AAS），則有BE=BF=12BD′=12BC，所以CE=BC-BE=12BC，從而△BCD為等腰三角形，故∠BCD=∠CBD=15°.

在圖11中，由已知條件得到∠ABD=∠ADB=75°，∠CBD=90°-75°=15°.把△ABD按圖11搬到BC邊上后，△ABD≌△BCD′.由∠ABD′=90°+30°=120°，∠A=30°，AB=BD′，可證A，D，D′三點(diǎn)共線，且△ABD′為等腰三角形.通過角度計(jì)算，可得∠DBD′=∠CD′D=45°.看到45°角學(xué)生自然會(huì)聯(lián)想到作高，分別過點(diǎn)C，D作AD′和BD′的高，垂足分別為E，F(xiàn)，從而證得△BFD≌△CED′.所以DF=CE.在Rt△DFD′中，因?yàn)椤螪D′F=30°，所以DF=12DD′，所以CE=12DD′，從而證得∠DCE=45°，故∠DCB=∠DCE-∠BCE=∠DCE-（∠BCD′-∠ECD′）=15°.

3 逆等線將軍飲馬例題

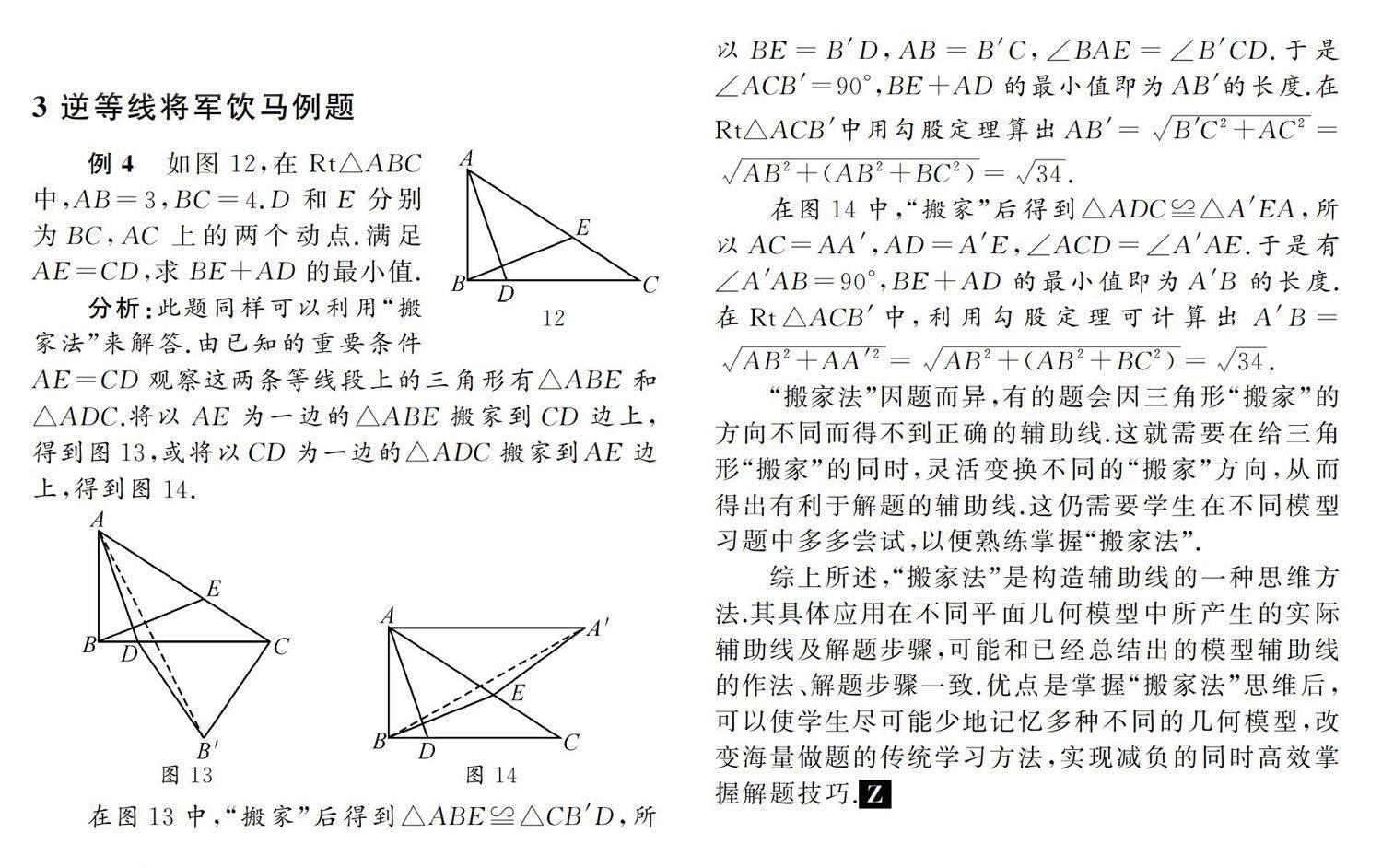
例4如圖12，在Rt△ABC中，AB=3，BC=4.D和E分別為BC，AC上的兩個(gè)動(dòng)點(diǎn).滿足AE=CD，求BE+AD的最小值.

分析：此題同樣可以利用“搬家法”來解答.由已知的重要條件AE=CD觀察這兩條等線段上的三角形有△ABE和△ADC.將以AE為一邊的△ABE搬家到CD邊上，得到圖13，或?qū)⒁訡D為一邊的△ADC搬家到AE邊上，得到圖14.

在圖13中，“搬家”后得到△ABE≌△CB′D，所以BE=B′D，AB=B′C，∠BAE=∠B′CD.于是∠ACB′=90°，BE+AD的最小值即為AB′的長度.在Rt△ACB′中用勾股定理算出AB′=B′C2+AC2=AB2+（AB2+BC2）=34.

在圖14中，“搬家”后得到△ADC≌△A′EA，所以AC=AA′，AD=A′E，∠ACD=∠A′AE.于是有∠A′AB=90°，BE+AD的最小值即為A′B的長度.在Rt△ACB′中，利用勾股定理可計(jì)算出A′B=AB2+AA′2=AB2+（AB2+BC2）=34.

“搬家法”因題而異，有的題會(huì)因三角形“搬家”的方向不同而得不到正確的輔助線.這就需要在給三角形“搬家”的同時(shí)，靈活變換不同的“搬家”方向，從而得出有利于解題的輔助線.這仍需要學(xué)生在不同模型習(xí)題中多多嘗試，以便熟練掌握“搬家法”.

綜上所述，“搬家法”是構(gòu)造輔助線的一種思維方法.其具體應(yīng)用在不同平面幾何模型中所產(chǎn)生的實(shí)際輔助線及解題步驟，可能和已經(jīng)總結(jié)出的模型輔助線的作法、解題步驟一致.優(yōu)點(diǎn)是掌握“搬家法”思維后，可以使學(xué)生盡可能少地記憶多種不同的幾何模型，改變海量做題的傳統(tǒng)學(xué)習(xí)方法，實(shí)現(xiàn)減負(fù)的同時(shí)高效掌握解題技巧.